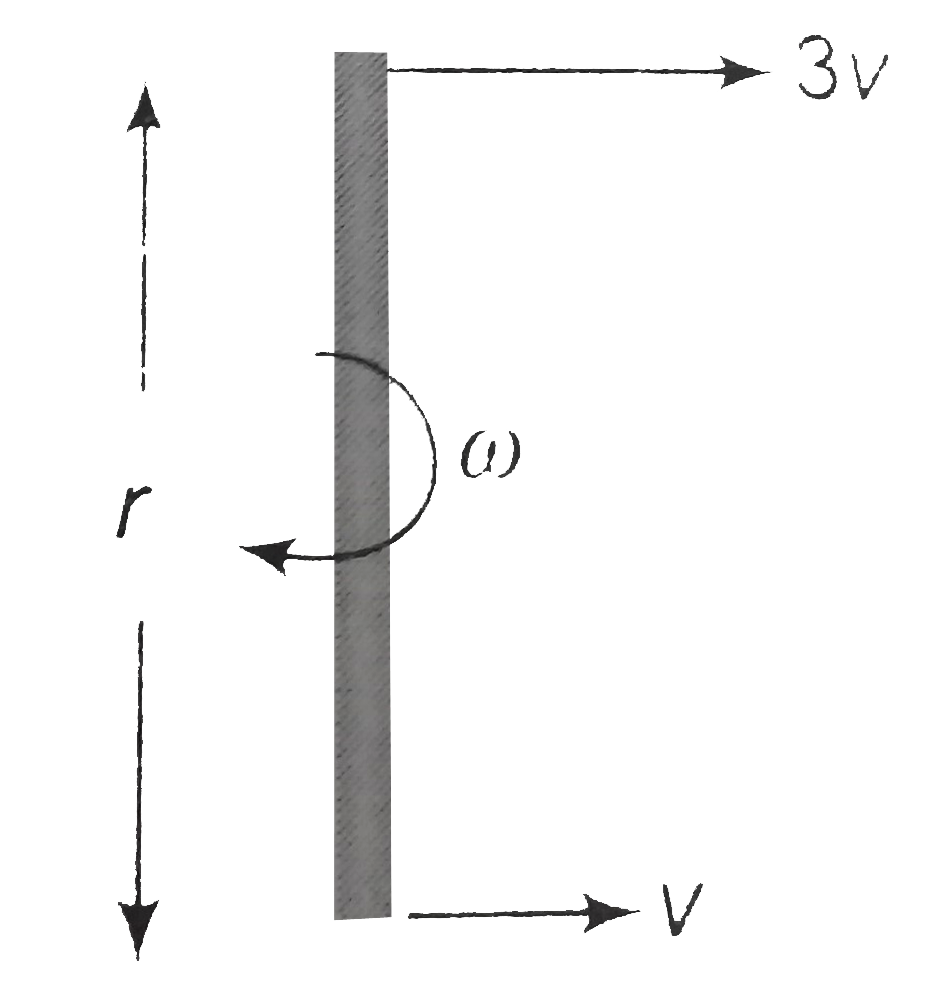
Two points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction, separated by a distance r. Then the angular velocity of the rod is :
3vr
4vr
5vr
2vr
The correct Answer is:D
(d) ωrad=ωp∮=(vrelr),vrel. Being the velocity of one point w.r.t. other.
=3v−vr and 'r' being the distance between them.
=2vr.
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Torque , Torque Equation And Equilibrium Of A Rigid Body
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation
30 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia
39 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
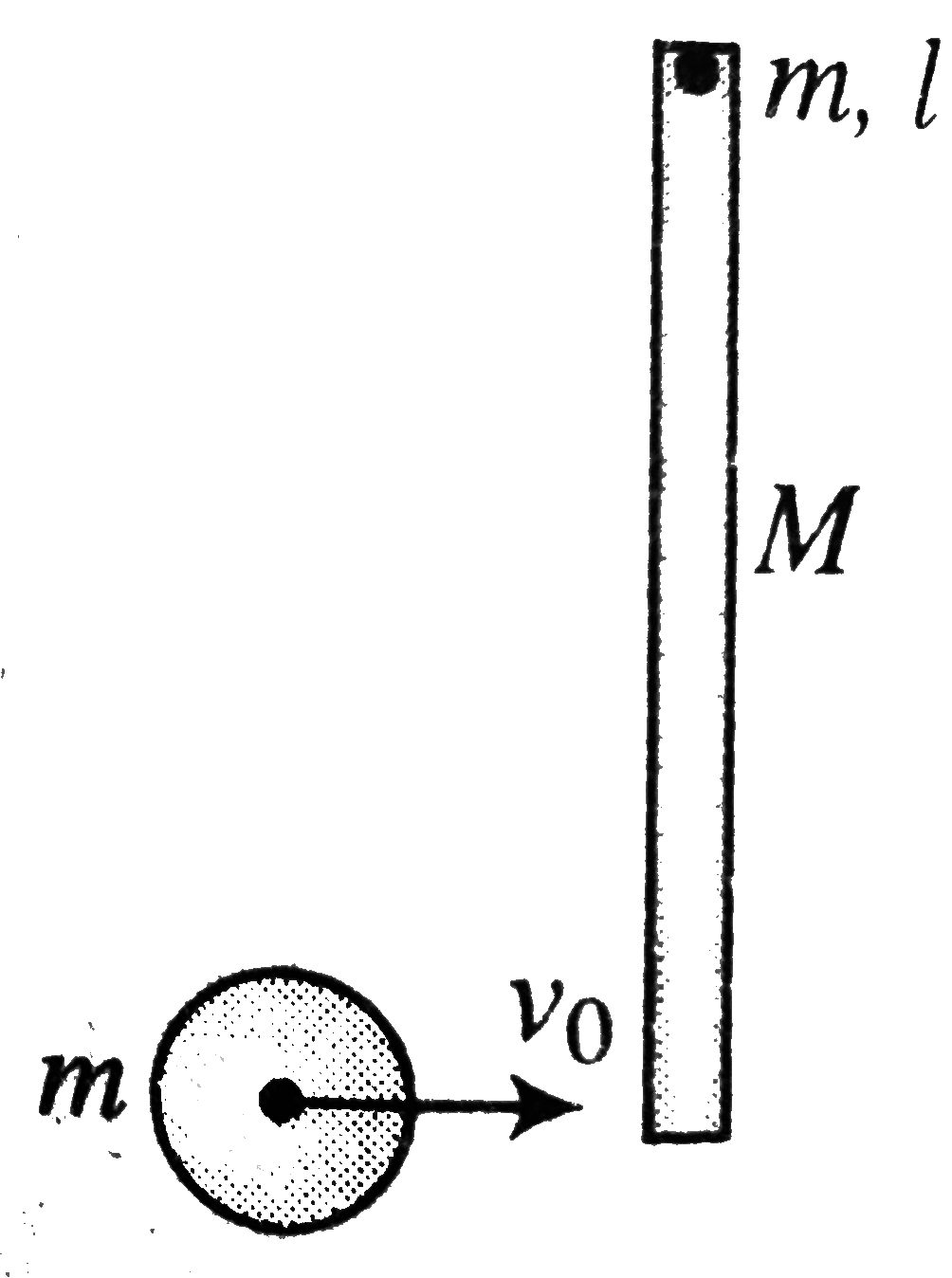
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
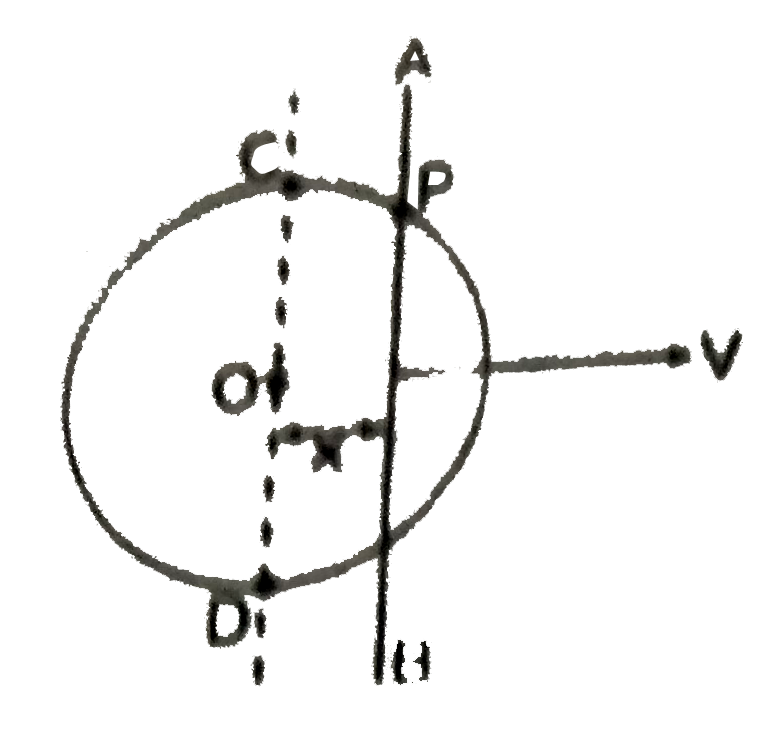
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View Solution
Knowledge Check
A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pmlA uniform rod of mass M=6m and length L is at rest on a frictionless surface. Two particles of mass 2m and 4m, moving with velocity v2m/s and v4m/s respectively strikes perpendicular to the rod form the same direction at its extreme ends and sticks to the rod. Find the distance travelled by the rod in time t.
Avt6Bvt4CvtD6vtA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07L
A uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angular velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA rod AB is moving on a fixed circle of radius R=5m with constant velocity v=4m/s as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from center of the circle. The velocity of the rodf is perpendicular to its lenght and the rod is always paraller to the diameter (CD)
Speed of point of intersection P is

View SolutionA small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View SolutionA cionducing rod moves with constant velocity v perpendicular to the straight wire carrying a current I as shown compute that the emf generated between the ends of the rod
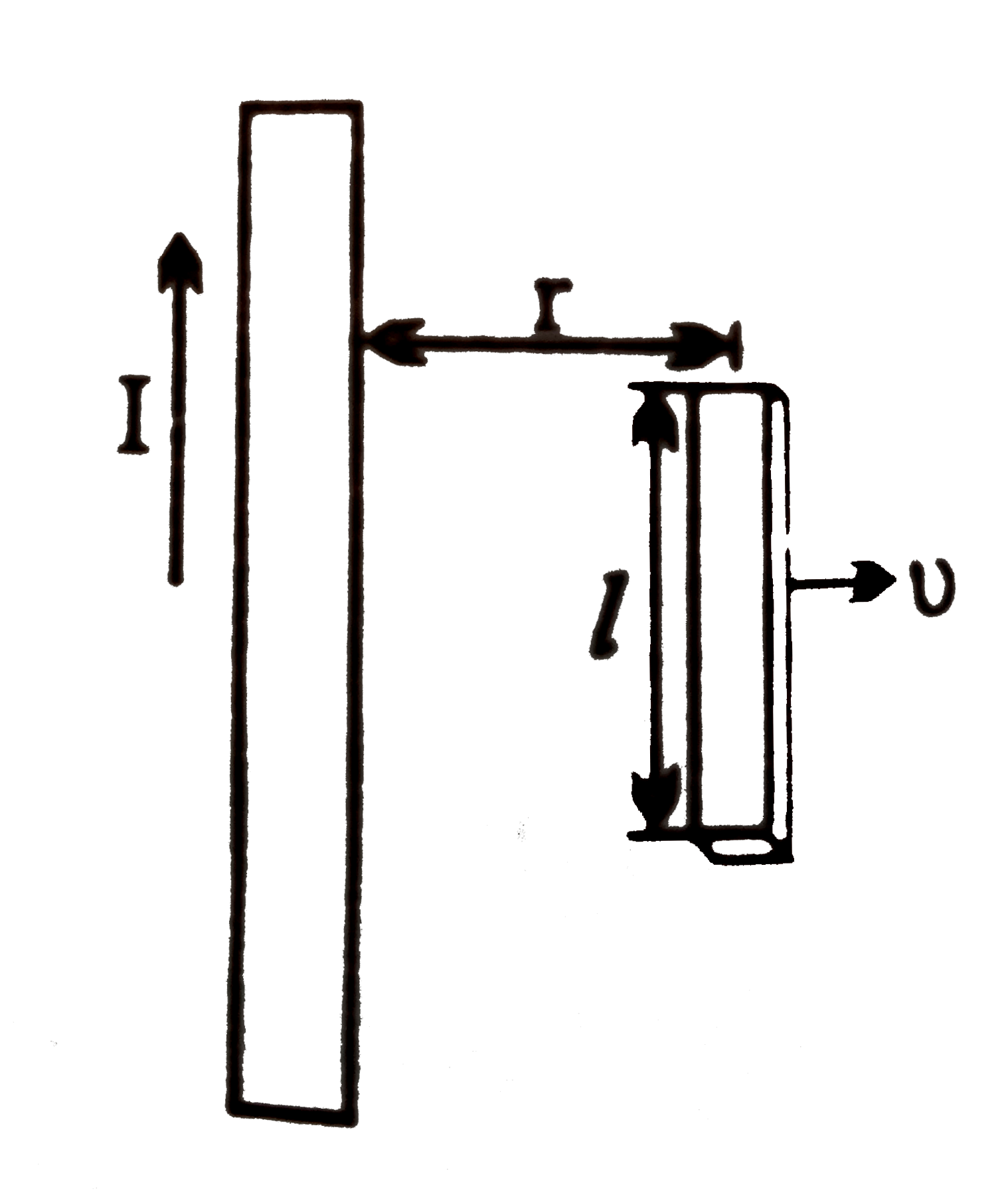
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
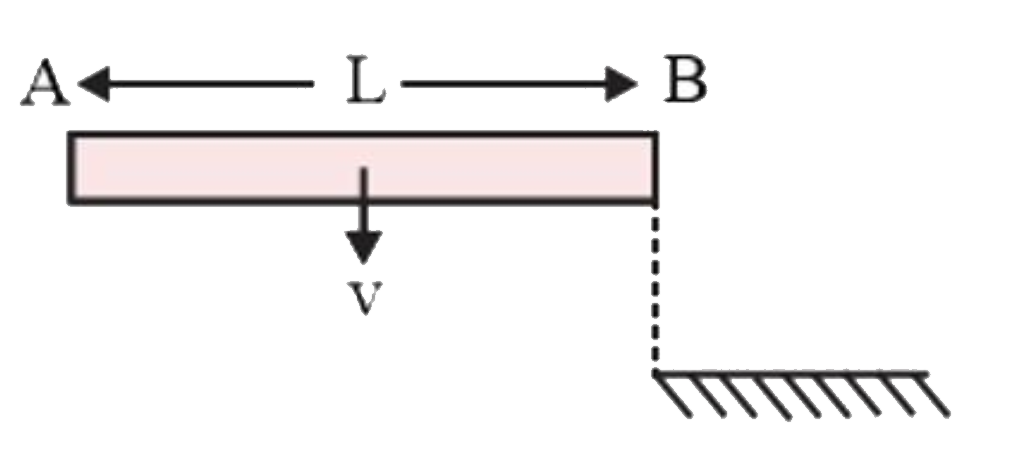
View Solution
