Two rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
K1d1+K2d2
K1+K2
K1d1+K2d2d1+d2
d1+d2d1K1+(d2K2)
The correct Answer is:D
Consider the diagram where two rods are connected end to end (series).
Thermal resistance (R ) of a rod of length l, thermal conductivity K and area of cross-section A is given by
R=lKA
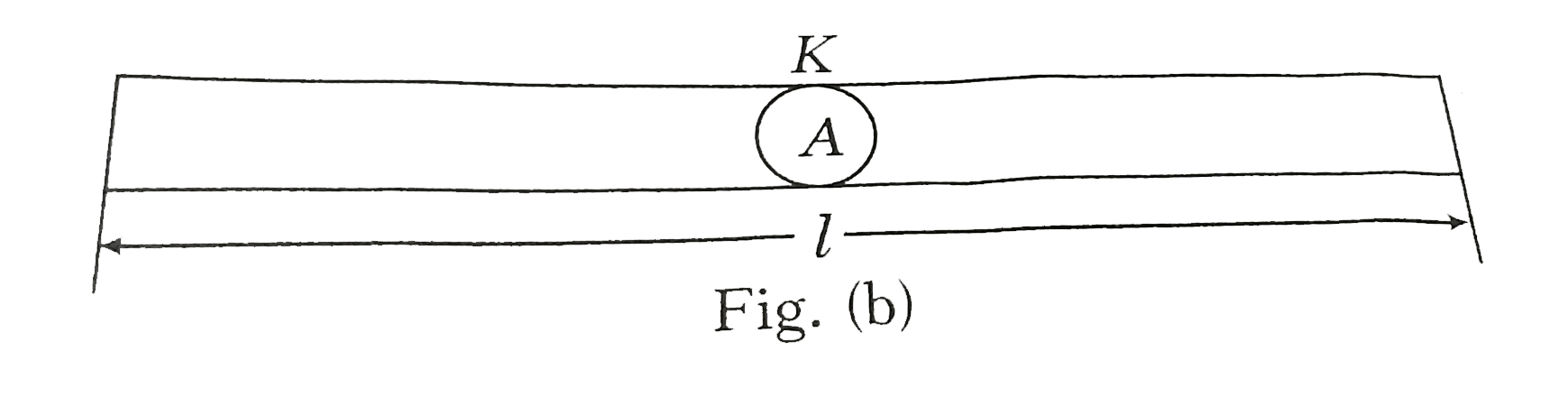
When rods are connected in series
Req = equivalent thermal resistance = R1+R2..............(i)
where, R1= Thermal resistance of first rod
R2 = thermal resistance of second rod
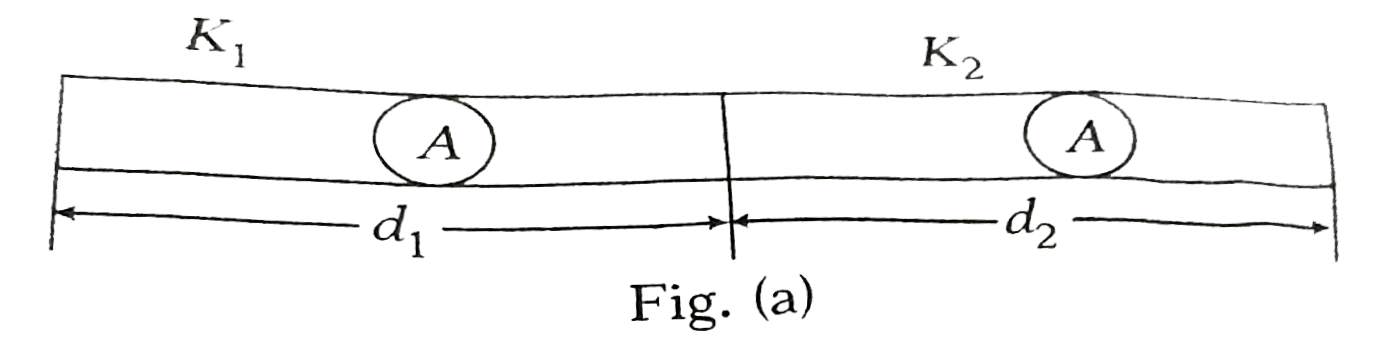
For fig. (a).
Thermal resistance of first rod, R1= (d_(1)/(K_(1)A)<br>Where,Aisareaofcross−sectionofeachrod.Similarly,thermalresistanceofsecondrod,R_(2)=d_(1)/(K_(2)A)<br>Now, From fig. a) Req=d1K1A+d2K2A
⇒(LeqKeqAeq = d1K1A□+d2K2A..........(ii)
where, Leq = equivalent length of rod
Eeq = equivalent are of cross-section .
For series connection,
Leq = equivalent length =d1+d2
Aeq = equivalent area of cross-section area = A
Now, from fig (b),
d1+d2KeqA=d1K1A+d2K2A⇒d1+d2Keq=d1K1+d2K2
⇒Keq=(K1K2K2d1+K2d2)(d1+d2)=d1+d2(d1K1+(d2K2))
[Dividing numerator and denomintator by K1K2]
Equivalent thermal conductivity, Keq=d1+d2(d1K1+d2K2)
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Define coefficient of thermal conductivity. Two metal slabs of same area of cross-section, thickness d1 and d2 having thermal conductivities K1 and K2 respectively are kept in contact. Deduce expression for equivalent thermal conductivity.
View SolutionTwo identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
View Solution
Knowledge Check
A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity k1 and k2. The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-
 AK1+K22B2K1+K2K1+K2CK1+K23D3K1+K2K1+K2
AK1+K22B2K1+K2K1+K2CK1+K23D3K1+K2K1+K2A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity k1 and k2. The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-
 AK1+K2B(K1+K2)2CK1+K2K1+K2D2K1+K2K1+K2
AK1+K2B(K1+K2)2CK1+K2K1+K2D2K1+K2K1+K2A wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity k1 and k2. The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-
 AK1+K2B(K1+K2)2CK1K2K1+K2D2K1+K2K1+K2
AK1+K2B(K1+K2)2CK1K2K1+K2D2K1+K2K1+K2
A composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivites K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionTwo rods of the same area of cross-section, but of length l1 and l2 and conductivites K1 and K2 are joined in series. Show that the combination is equivalent of a material of conductivity K=l1+l2(l1K2)+(l2K2)
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionIf two metallic plates of equal thickness and thermal conductivities K1 and K2 are put together face to face and a common plate is constructed, then the equivalent thermal conductivity of this plate will be

View Solution Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
