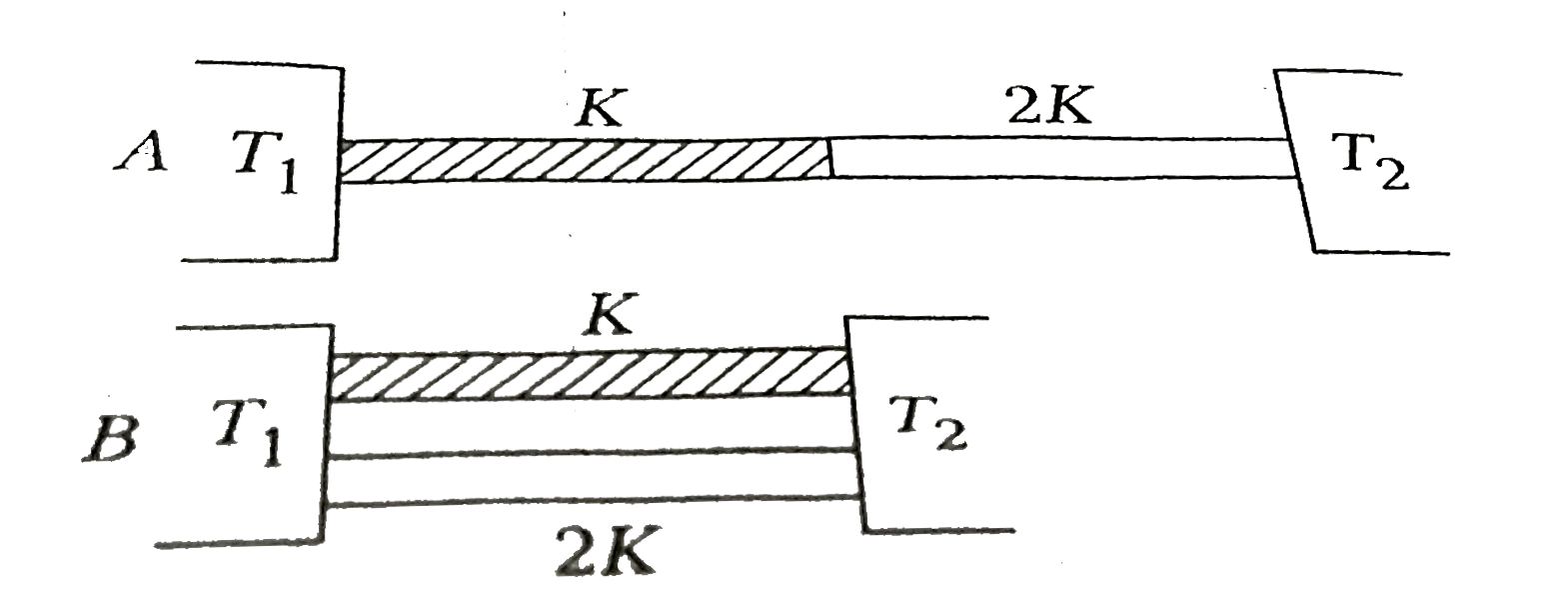
Two rods with the same dimensions have thermal conductivities in the ratio 1 : 2. they are arranged between heat reservoirs with the same temperature difference, in two different configurations, A and B. The rates of heat flow in A and B are IAandIB respectively. The ratio IAIB) is equal to
1:2
1:3
2:5
2:9
The correct Answer is:D
Rate of heat flow lαTDR
(H = Temperature difference between two points//R)
As TD = temperature difference is same.
∴ I α(1)/(Thermal resistance)
IAIB=RBRA = ((R)(2R)//R+2R)/(R+2R) = 2/9
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
25 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
If two conducting wires A and B of same dimensions have electron density ratio 1: 3 . If their relaxation time is same then the ratio of resistance of A to resistance of B is
View SolutionTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
View Solution
Knowledge Check
Two identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is
 Aθ1+θ22BK1θ1+K2θ2K1+K2CK1θ2+K2θ1K1+K2DK1θ1+K2θ2[K1−K2]
Aθ1+θ22BK1θ1+K2θ2K1+K2CK1θ2+K2θ1K1+K2DK1θ1+K2θ2[K1−K2]Two cylindrical conductors A and B of same metallic material have their diameters in the ratio 1:2 and lengths in the ratio 2:1. If the temperature difference between their ends is same, the ratio of heats conducted respectively by A and B per second is,
A1:2B1:4C1:16D1:8The ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals−1. What is the rate of flow of heat in the larger rod:
A1cals−1B4cals−1C8cals−1D16cals−1
The end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionThe three rods described in the previous question are placed individually, with their ends kept at the same temperature difference. The rate of heat flow through C is equal to the rate of combined heat flow through A and B. kc must be equal to
View SolutionTwo liquids A and B of equal volumes have their specific heats in the ration2:3. If they have same thermal capacity, then the ratio of their densities is
View SolutionTwo wires A and B of same material and mass have their lengths in the ratio 1:2. On connecting them to the same source, the rate of heat dissipation in B is found to be 5 W . The rate of heat dissipation in A is
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View Solution
