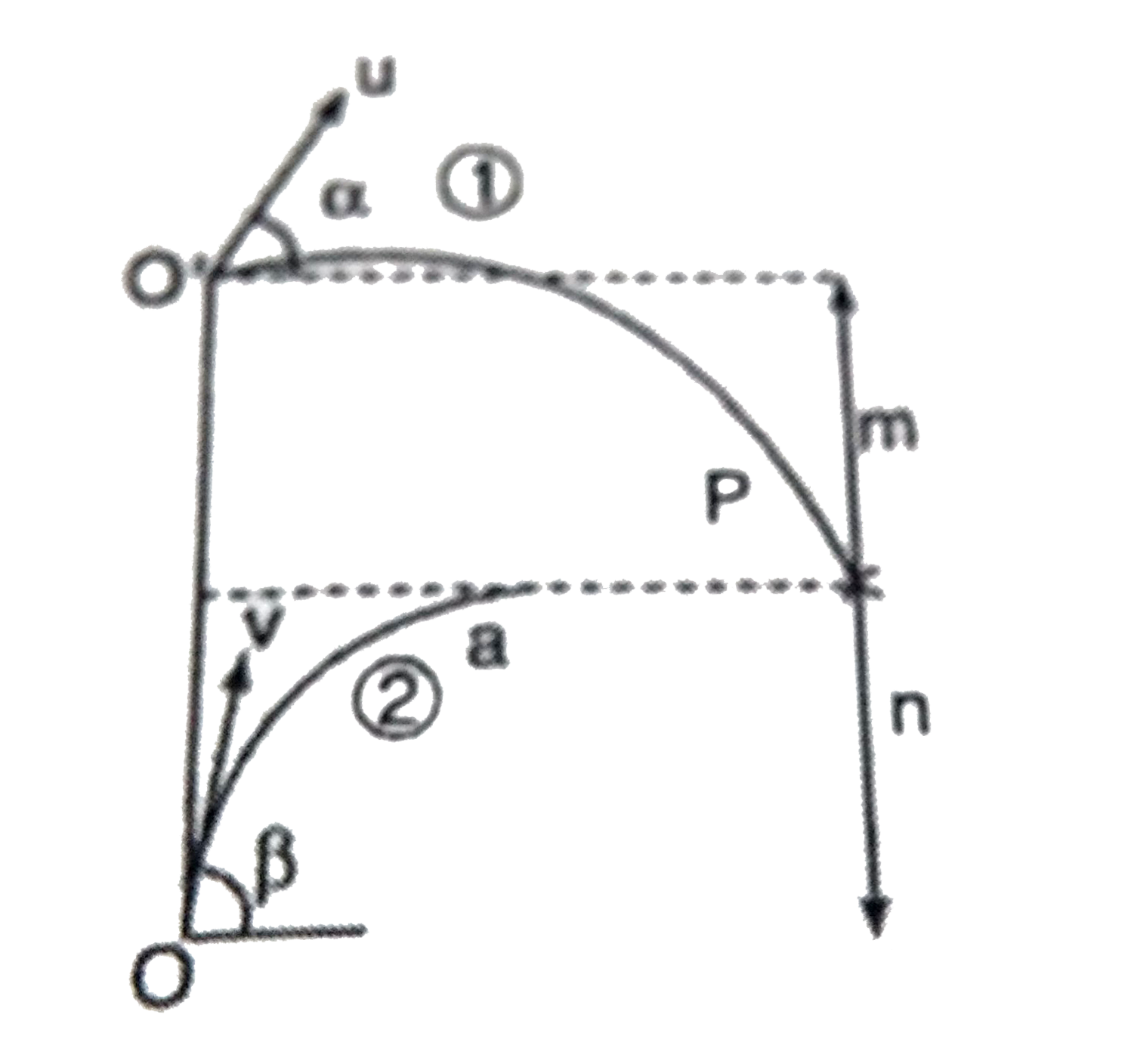
Two shells are fired from a canon with seped (u) each, at angles if $α$ and $β$ respectively with the horizontal . The time intrval between the shots is (t). They collide in mid air after time (T) from the first shot . Which of the following consitions must be satisfied ?

A

$α > β$

B

$T cos α = (T - t) cos β$

C

$T - t) cos α = T cos β$

D

$u sin α T - \frac{1}{2} g T^{2} = u sin b w t a (T - t) - \frac{1}{2} {g (T - t)}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

Since the first shot must have travelled for more time than the second shot before collinding in mid air. It will be so if the angle of projection of first short $α$ is greater than the angle of projection of second shot $β i . e . α > β$ .
At the colliding position of two shots , the borizontal distance (x) covereed by each shot is same so $x = u cos α T = u cos β (T - t)$
or $T cos α = (T - t) cos β$
At the colliding position of two shots, the vertical distance (y) covered by first shot is
$y = u sin α t - \frac{1}{2} g T^{2}$
The verrtical distance $y$ covered by secnd shot is
$y = u sin β (T - t) - \frac{1}{2} {g (T - t)}^{2}$
:. $u sin α T - \frac{1}{2} g T^{2} = u sin β (T - t) - \frac{1}{2} {g (T - t)}^{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two shells are fired from a cannot with a speed u each, at angles of $α$ and $β$ respectively to the horizontal. The time interval between the shots is T. they collide in mid-air after time t from the first shot. Which of the following conditions must be satisfied ?
A $α > β$
B $t cos α = (t - T) cos β$
C $(t - T) cos α = t cos β$
D $(u sin α) t - \frac{1}{2} g t^{2} = (u sin β) (t - T) - \frac{1}{2} {g (t - T)}^{2}$
Question 2 - Select One or More
Two shells are fired from cannon with speed $u$ each, at angles of $α$ of $β$ respectively with the horizontal.The time interval between the shots is $T$ .They collide in mid air after time $t$ from the first shot.Which of the following conditions must be satisfied?
A $α > β$
B $t cos α = (t - T) cos β$
C $(t - T) cos α = t cos β$
D $(u sin α) t - \frac{1}{2} {gt}^{2} = (u sin β) (t - T) - \frac{1}{2} {g (t - T)}^{2}$
Question 3 - Select One or More
Two shells are fired from a canon successively with speed u each at angles of projection $α and β$ , respectively. If the time interval between the firing of shells is dt and they collide in mid-air after a time t from the firing of the first shell. Then
A $t cos α = (t - d t) cos β$
B $α > β$
C $(t - d t) cos α = d t cos β$
D $(u sin α) t - \frac{1}{2} g {d t}^{2} = (u sin β) t - d t - \frac{1}{2} {g (t - d t)}^{2}$

PRADEEP-KINEMATICS-3 NCERT multiple

Home
Ask Doubt
Profile