Two SHM particles P1 and p2 start from +A2 and −√3A2, both in negative directions. Find the time (in terms of T) when they collide. Both particles have same omega, A and T and the execute SHM along the same line.
The correct Answer is:A
To find the time when the two SHM particles P1 and P2 collide, we can follow these steps:
Step 1: Understand the Initial Positions
The initial positions of the particles are given as:
- Particle P1 starts from +A2
- Particle P2 starts from −√3A2
Both particles are moving in the negative direction.
Step 2: Determine the Angles for Each Particle
Using the cosine function, we can find the angles corresponding to the initial positions of both particles.
For P1:
cos(α)=Position of P1A=A2A=12
Thus,
α=cos−1(12)=π3 (or 60 degrees)
For P2:
cos(β)=Position of P2A=−√3A2A=−√32
Thus,
β=cos−1(−√32)=5π6 (or 120 degrees)
Step 3: Find the Condition for Collision
The two particles will collide when they reach the same position. Since they are moving in the same direction with the same angular frequency ω, the angle between them will be 90∘ (or π2) at the time of collision.
Step 4: Calculate the Total Angle Rotated
At the time of collision, the angle P1 has rotated from π3 to π2:
Angle rotated by P1=π2−π3=3π6−2π6=π6
Step 5: Calculate the Time Taken
Using the relationship between angle and time:
θ=ωt
Where ω=2πT. Thus,
π6=2πT⋅t
Rearranging gives:
t=π/6⋅T2π=T12
Final Answer
The time t when the two particles collide is:
t=T12
The initial positions of the particles are given as:
- Particle P1 starts from +A2
- Particle P2 starts from −√3A2
Using the cosine function, we can find the angles corresponding to the initial positions of both particles.
cos(α)=Position of P1A=A2A=12
Thus,
α=cos−1(12)=π3 (or 60 degrees)
cos(β)=Position of P2A=−√3A2A=−√32
Thus,
β=cos−1(−√32)=5π6 (or 120 degrees)
The two particles will collide when they reach the same position. Since they are moving in the same direction with the same angular frequency ω, the angle between them will be 90∘ (or π2) at the time of collision.
At the time of collision, the angle P1 has rotated from π3 to π2:
Angle rotated by P1=π2−π3=3π6−2π6=π6
Using the relationship between angle and time:
θ=ωt
Where ω=2πT. Thus,
π6=2πT⋅t
Rearranging gives:
t=π/6⋅T2π=T12
The time t when the two particles collide is:
t=T12
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 5
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 6
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 3
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
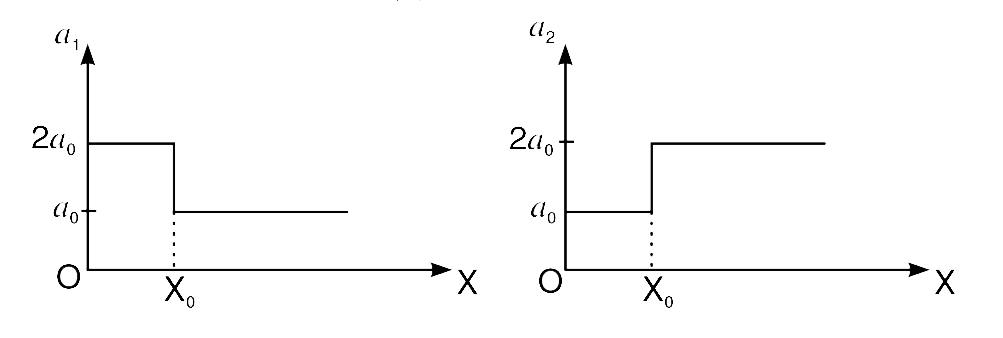
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
View SolutionA particle in SHM starts its journey (at t=0) from x=−A2 in negetive direction. Write x−t eqution corresponding to given condition. Angular freqency of oscillations is ω.
View Solution
Knowledge Check
Two particles P1 and P2 are performing SHM along the same line about the same meabn position , initial they are at their position exterm position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the seopration between the particle becomes 6cm
A5secB2secC4secD6secTwo particles executing SHM of same frequency, meet at x=+A/2, while moving in opposite direction . Phase difference between the particles is
Aπ6Bπ3C5π6D2π3A particle executing SHM of amplitude a has displacement a2 at t=T4 and a negative velocity. The epoch of the particle is
Aπ3B2π3CπD5π3
Two particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.
View SolutionTwo SHM's are represented by y1=Asin(ωt+ϕ),y2=A2[sinωt+√3cosωt]. Find ratio of their amplitudes.
View SolutionThe resultant of two S.H.M. having the same period T but different amplitudes and phases, along the same line is S.H.M
View SolutionA particle executed S.H.M. starting from its mean position at t=0, If its velocity is √3bω, when it is at a distance b from the mean positoin, when ω=2πT, the time taken by the particle to move from b to the extreme position on the same side is
View SolutionThe periodic times of two particles P and Q executing S.H.M. s are in the ration of 1 : 5. Both start moving from the mean position at the same ins"tan"t. After how many osicllations of P, the two particles will be again in phase at the mean position ?
View Solution
