Two short dipoles are placed perpendicularly as shown. Find electric field and potential at charge distance r.
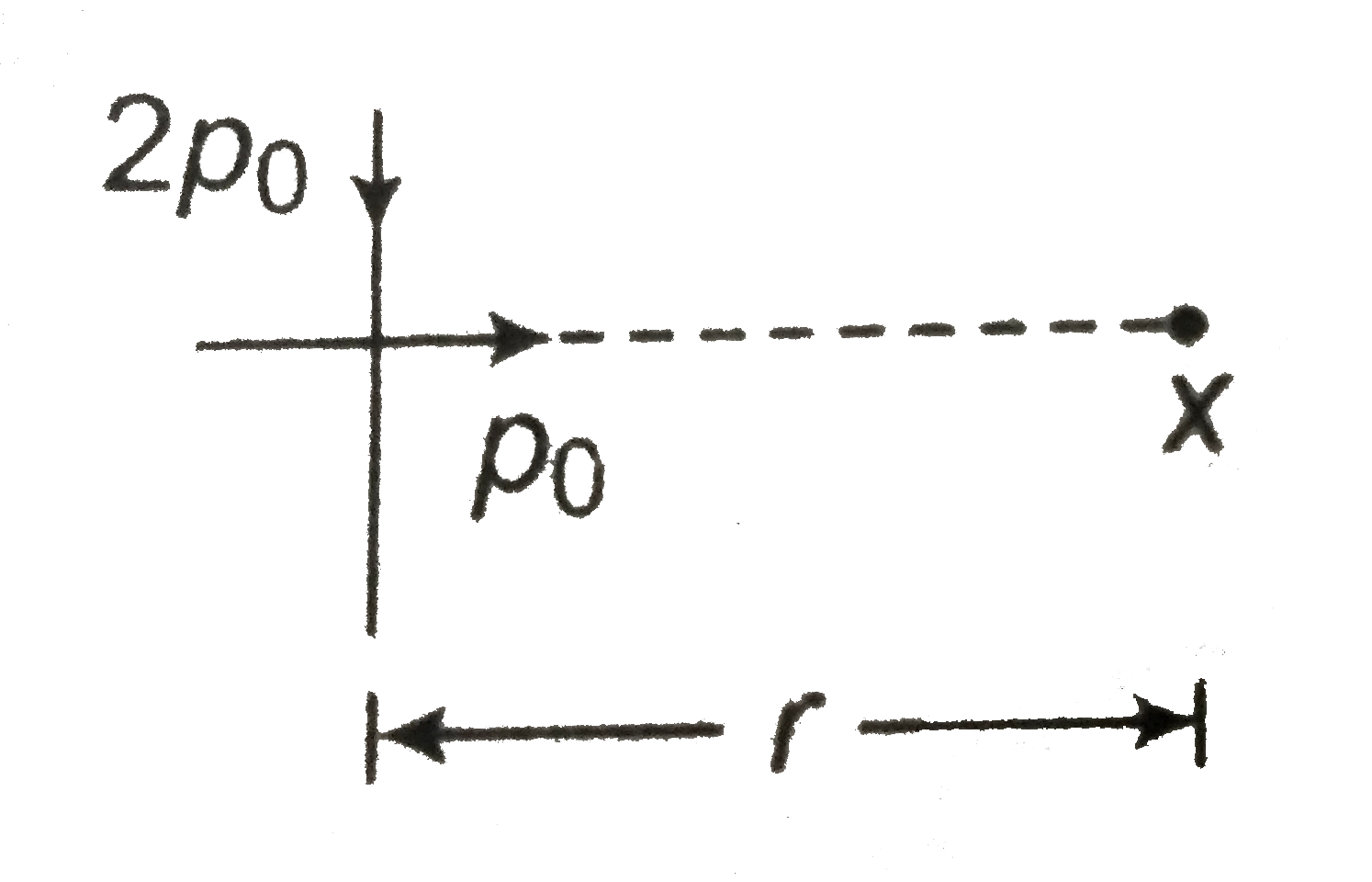
Electric field at P:
Due to ①,E1=14π∈0.2p0r3
Due to ②,E2=14π∈0.2p0r3
Ep=√E21+E22=14π∈02√2p0r3,θ=45∘
Electric potential at P:
Due to ①,V1=14π∈0.p0r2
Due to ②,V2=0
Vp=V1+V2=14π∈0.p0r2
Topper's Solved these Questions
Similar Questions
Charges are placed on the vertices of a square as shown. Let E r be the electric field and V the potential at the centre. If the charges on A and B are interchanged with those on D and C respectively, then :-

View SolutionInside a conducting hollow sphere of inner radius R1 and outer radius R2, a point charge q is placed at a distance x from the center as shown in (Fig. 3.70.) Find.
 .
.
(i) electric potential at C
(ii) electric field and potential at a distance r from the center outside the shell.
View Solution
Knowledge Check
For an electric dipole potential & electric field
Acan have same magnitude for a point at a distance less than 2 meterBcan have same magnitude fo a point at distacnes greater than 2 meterCcan never be equalDcan never be predictedThe electric field and the potential of an electric dipole vary with distance r as
A1r and 1r2B1r2 and 1rC1r2 and 1r3D1r3 and 1r2A point P lies on the perpendicular bisector of a short electric dipole, of dipole moment p' at a distance r from the centre of dipole. The electric field at point P is proportional to
APr2B1pr2Cpr3Dp2r3
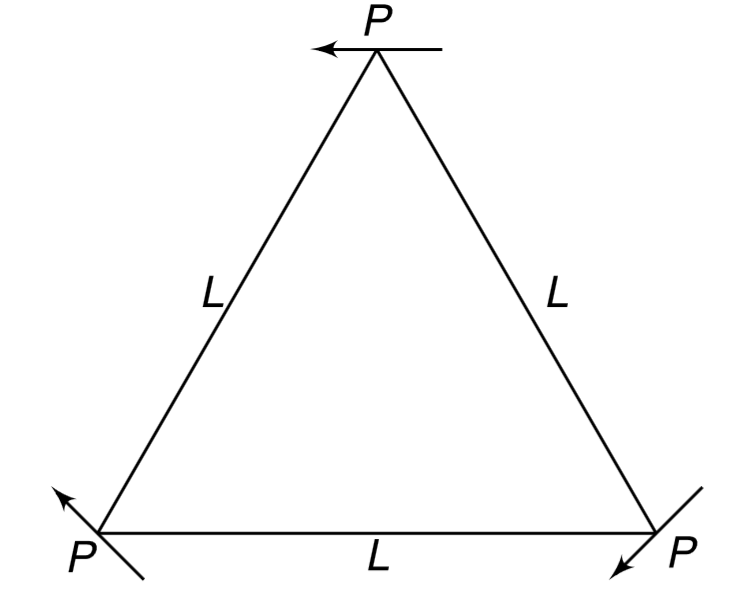
Three short electric dipoles, each of dipole moment P, are placed at the vertices of an equilateral triangle of side length L. Each dipole has its moment oriented parallel to the opposite side of the triangle as shown in the fig. Find the electric field and potential at the centroid of the triangle
View SolutionTwo short electric dipole are placed as shown. The energy of electric interaction between these dipole will be
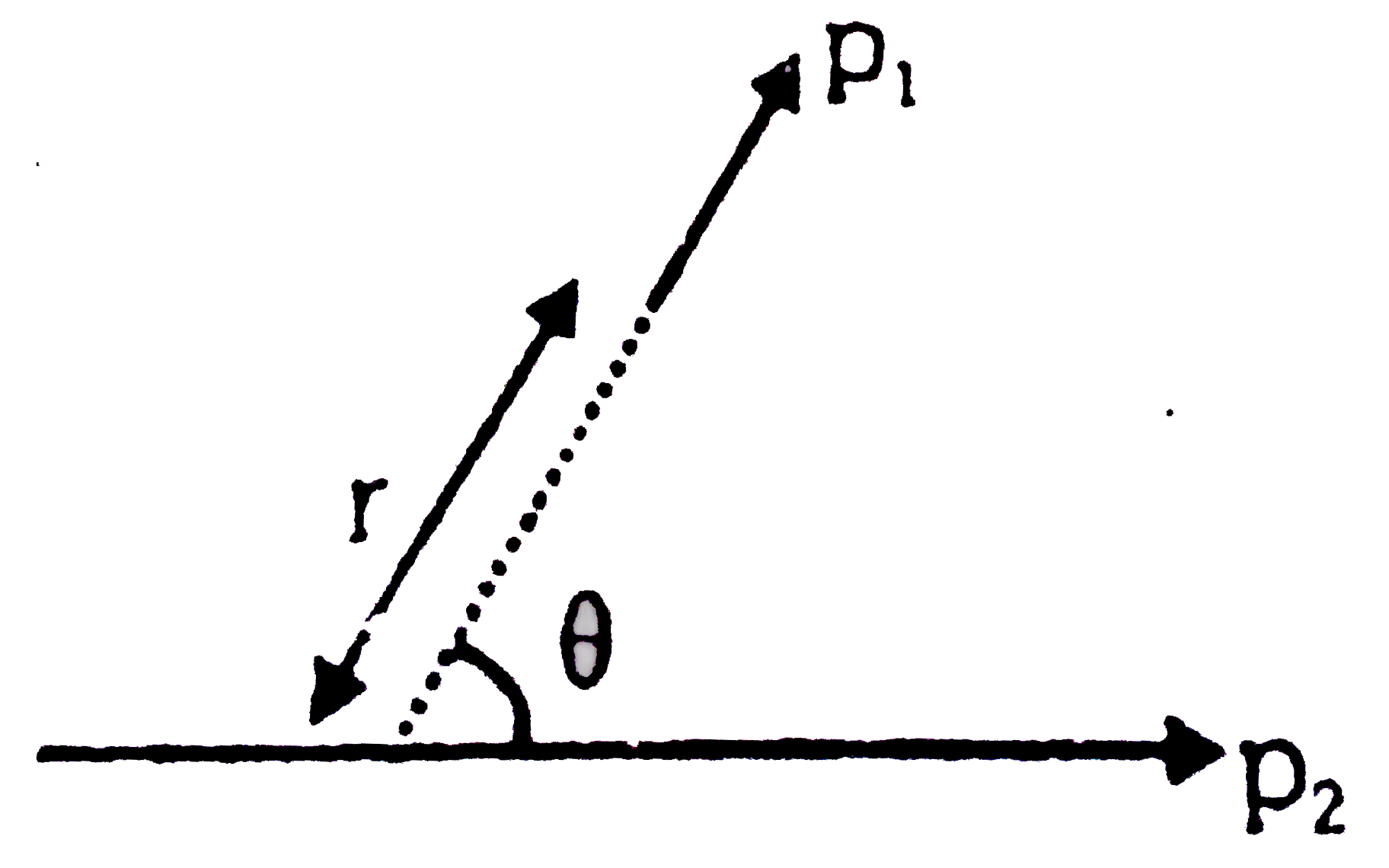
View SolutionTwo short electric dipoles are placed as shown in figure. Find the potential energy of electric interaction between these dipoles.
[−Kp1p2cosθr3]
View SolutionTwo short magnets of equal dipole moments M are fastened perpendicularly at their centres as shown in the figure. The magnitude of the magnetic field at a distance d from the centre on the bisector of the right angle is

View SolutionThe electric field and the potential of an electric dipole vary with distance 'r' as
View Solution
