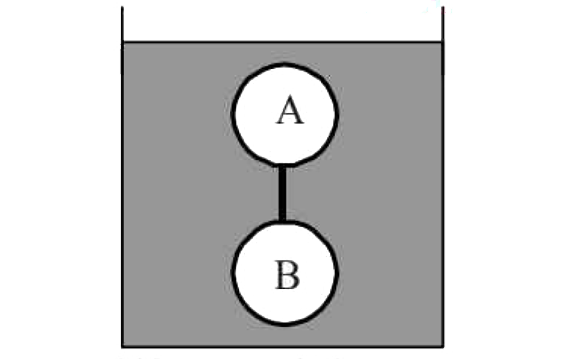
Two solid spheres A and B of equal volumes but of different densities are connected by a string. They are fully immersed in a fluid of density . They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
The correct Answer is:A, B, D
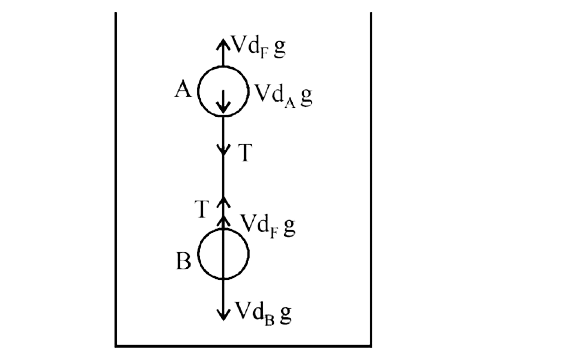
(a,b,c) Let V be the volume of shperes.
For equilibrium of A:
(a) is the correct option
For equilibrium of B:
(b) is the correct option
From (1) & (2) Vg
(d) is the correct option.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Two spheres of volume 250 cc each but of relative densities 0.8 an d 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension I the string. (g=10m/s2)
View SolutionTwo solid sphere (A and B) are made of metals of different densities ρA and ρB respectively. If their masses are equal, the ratio of their moments of inertia (IAIB) about their respective diameter is
View Solution
Knowledge Check
Three equal weight A,B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is approximately
 AzeroB13NC3.3ND19.6N
AzeroB13NC3.3ND19.6NIn the arrangement as shown, A and B arc two cylinders each of length L and density d1 and d2(d1<d2) respectively. They are joined together and submerged in the liquid of density d with length L/2 of A outside the liquid. If the difference in densities of two cylinders is equal to density of the liquid, find d1.
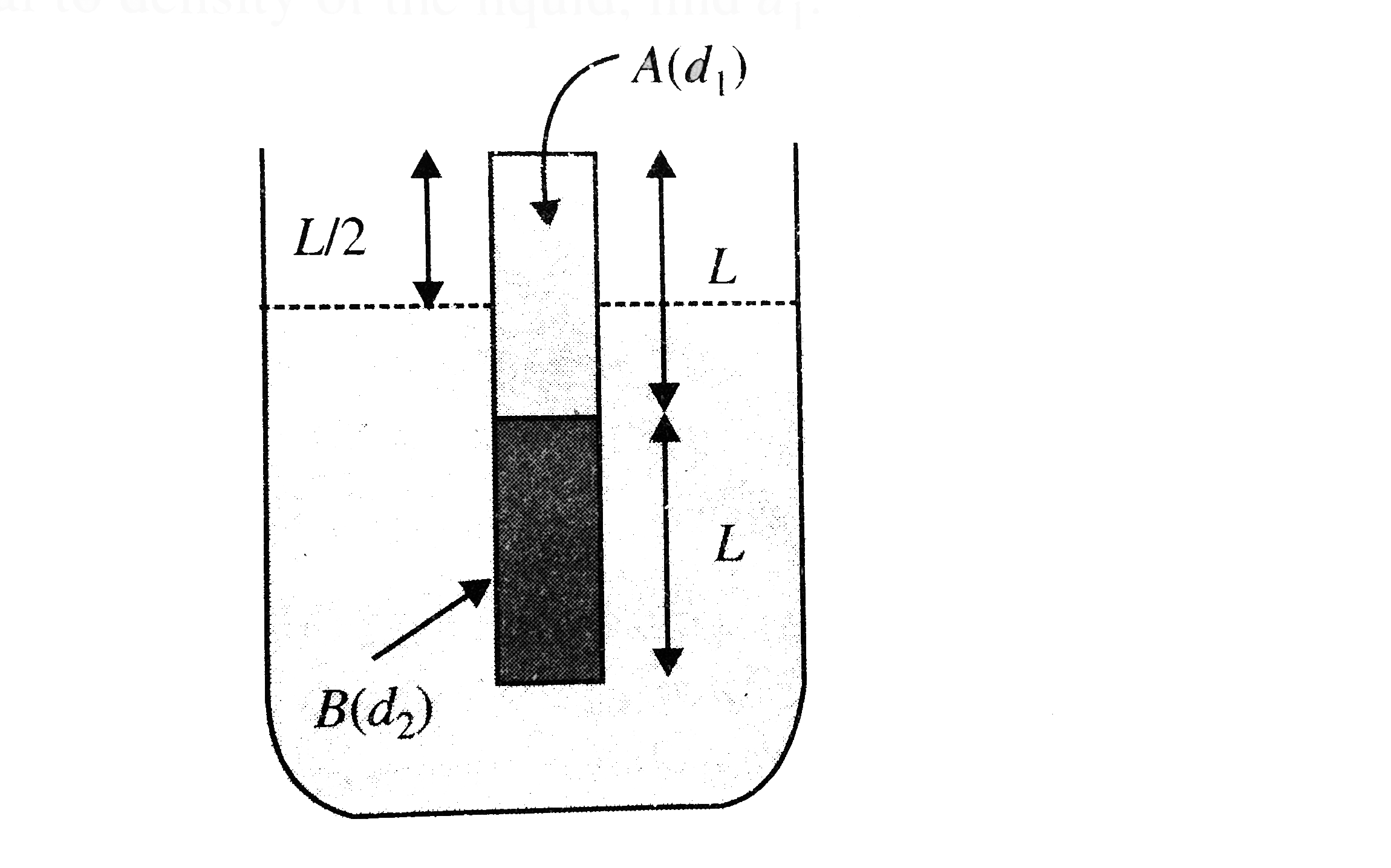 A54dBd4C34dDd2
A54dBd4C34dDd2
If a body of volume V is immersed in a liquid of density d and g is acceleration due to gravity, then upthrust FB= ______.
View SolutionIn the arrangement of resistances shown in figure. Find the value of unknown resistance X if the potential difference between B and D is zero.
View SolutionIn the pulley system shown the movable pulleys A,B and C have mass m each, D and E are fixed pulleys. The strings are vertical light and inextensible Then
 .
.
View SolutionA,A,B,B,C,C,D,E,F are arranged in a row so that no two alike alphabets are together. Find number of such arrangment
View SolutionThe number of different triangles formed by joining the points A,B,C,D,E,FandG as shown in the figure given below is
View SolutionTwo particle of masses 10 kg and 35 kg are connected with four strings at points B and D as shown in fig.

Determine the tension in various segments of the string.
View Solution
