Two solid uniform spheres each of radius 5 cm are connected by a light and totally immersed in a tank of water. If the specific gravities of the pressure are 0.5 and 2, find the tension in the string and the contact force between the bottom of the tank and the heavier sphere.
To solve the problem, we will follow these steps:
Step 1: Identify the parameters
- Radius of each sphere, r=5cm=0.05m
- Specific gravity of the first sphere (lighter), SG1=0.5 (density ρ1=0.5g/cm3=500kg/m3)
- Specific gravity of the second sphere (heavier), SG2=2 (density ρ2=2g/cm3=2000kg/m3)
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the volume of each sphere
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the radius:
V=43π(0.05)3=43π(1.25×10−5)≈5.24×10−5m3
Step 3: Calculate the weight of each sphere
Weight W is given by:
W=mass×g=V×density×g
- For the lighter sphere:
W1=V×ρ1×g=5.24×10−5×500×10=2.62N
- For the heavier sphere:
W2=V×ρ2×g=5.24×10−5×2000×10=10.48N
Step 4: Calculate the buoyant force acting on each sphere
The buoyant force Fb is equal to the weight of the water displaced by the volume of the sphere:
Fb=V×density of water×g
For water, the density is 1000kg/m3:
Fb1=V×1000×10=5.24×10−5×1000×10=0.524N
Fb2=V×1000×10=0.524N
Step 5: Set up equations for tension and normal force
For the lighter sphere:
Fb1−T−W1=0⟹T=Fb1−W1=0.524−2.62=−2.096N (not possible, so T = 0)
For the heavier sphere:
W2−T−Fb2=N⟹10.48−T−0.524=N
Substituting T=0:
N=10.48−0.524=9.956N
Step 6: Final Results
- Tension in the string, T=0N
- Contact force between the bottom of the tank and the heavier sphere, N≈9.956N
- Radius of each sphere, r=5cm=0.05m
- Specific gravity of the first sphere (lighter), SG1=0.5 (density ρ1=0.5g/cm3=500kg/m3)
- Specific gravity of the second sphere (heavier), SG2=2 (density ρ2=2g/cm3=2000kg/m3)
- Acceleration due to gravity, g=10m/s2
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the radius:
V=43π(0.05)3=43π(1.25×10−5)≈5.24×10−5m3
Weight W is given by:
W=mass×g=V×density×g
- For the lighter sphere:
W1=V×ρ1×g=5.24×10−5×500×10=2.62N
- For the heavier sphere:
W2=V×ρ2×g=5.24×10−5×2000×10=10.48N
The buoyant force Fb is equal to the weight of the water displaced by the volume of the sphere:
Fb=V×density of water×g
For water, the density is 1000kg/m3:
Fb1=V×1000×10=5.24×10−5×1000×10=0.524N
Fb2=V×1000×10=0.524N
For the lighter sphere:
Fb1−T−W1=0⟹T=Fb1−W1=0.524−2.62=−2.096N (not possible, so T = 0)
W2−T−Fb2=N⟹10.48−T−0.524=N
Substituting T=0:
N=10.48−0.524=9.956N
- Tension in the string, T=0N
- Contact force between the bottom of the tank and the heavier sphere, N≈9.956N
Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - practice Exercise 7.1
10 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Practice Exercise 7.2
8 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
A solid sphere of radius 5 cm floats in water. If a maximum load of 0. kg can be put on it withot wetting the load find the specific gravityof the material of the sphere.
View SolutionA sphere of radius R, made from material of specific gravity SG, is submerged in a tank of water. The sphere is placed over a hole, of radius a, in the tank bottom. For the dimensions given, determine the minimum SG required for the sphere to remain in the position shown.
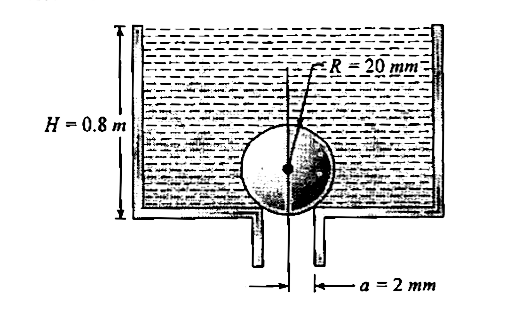
View Solution
Knowledge Check
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, find the uniform thickness of the cylinder.
A2 cmB3 cmC1 cmD3.5 cmA solid metal sphere is cut through its centre into two equal parts . Find the total surface area of each part if the radius of the sphere is 7 cm.
A462cm2B231cm2C308cm2D115.5cm2Two smooth sphere each of radius 5cm and weight W rest one on the other inside a fixed smooth cylinder of radius 8cm. The reaction between the sphere and the vertical side of the cylinder are:
 AW/4 and 3W/4BW/4 and W/4C3W/4 and 3W/4DW and W
AW/4 and 3W/4BW/4 and W/4C3W/4 and 3W/4DW and W
Two spheres of volume 250 cc each but of relative densities 0.8 an d 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension I the string. (g=10m/s2)
View SolutionA sphere of radius 5cm is immersed in water filled in a cylinder, the level of water rises 53cm. Find the radius of the cylinder.
View SolutionTwo spheres of masses 2.6 kg and 4.1 kg are tied together by a light string looped over a frictionless pulley.
(i) What will the acceleration of each mass be?
(ii) Find the value of tension in the string.
View SolutionA solid sphere of mass m=2kg and specific gravity s=0.5 is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water =1000kgm−3,g=10ms−2).
 .
.
View SolutionA solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)

View Solution
