Two spring P and Q having stiffness constants and , respectively are stretched equally. Then
(a) More work is done on Q
(b) More work is done on P
(c) Their force constants will become equal
(d) Equal work is done on both the springs
The correct Answer is:B
To solve the problem, we need to analyze the work done on two springs P and Q when they are stretched equally. The springs have stiffness constants k1 and k2 respectively, where k2<k1.
1. Understanding the Force on Each Spring:
The force exerted by a spring when it is stretched is given by Hooke's Law:
F=k⋅x
where F is the force, k is the stiffness constant, and x is the elongation (displacement).
2. Calculating Forces for Springs P and Q:
- For spring P (with stiffness constant k1):
FP=k1⋅x
- For spring Q (with stiffness constant k2):
FQ=k2⋅x
3. Comparing the Forces:
Since k2<k1, it follows that:
FP>FQ
This means that the force exerted by spring P is greater than that exerted by spring Q when both are stretched by the same amount x.
4. Calculating Work Done on Each Spring:
The work done on a spring when it is stretched is given by:
W=F⋅x
- For spring P:
WP=FP⋅x=(k1⋅x)⋅x=k1⋅x2
- For spring Q:
WQ=FQ⋅x=(k2⋅x)⋅x=k2⋅x2
5. Comparing the Work Done:
Since k1>k2, it follows that:
WP>WQ
Therefore, more work is done on spring P than on spring Q.
Conclusion:
The final answer is that more work is done on spring P.
The force exerted by a spring when it is stretched is given by Hooke's Law:
F=k⋅x
where F is the force, k is the stiffness constant, and x is the elongation (displacement).
- For spring P (with stiffness constant k1):
FP=k1⋅x
- For spring Q (with stiffness constant k2):
FQ=k2⋅x
Since k2<k1, it follows that:
FP>FQ
This means that the force exerted by spring P is greater than that exerted by spring Q when both are stretched by the same amount x.
The work done on a spring when it is stretched is given by:
W=F⋅x
- For spring P:
WP=FP⋅x=(k1⋅x)⋅x=k1⋅x2
- For spring Q:
WQ=FQ⋅x=(k2⋅x)⋅x=k2⋅x2
Since k1>k2, it follows that:
WP>WQ
Therefore, more work is done on spring P than on spring Q.
The final answer is that more work is done on spring P.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
This question has statement 1 and statement 2 . Of the four choice given after the Statement , choose the one that best describe the two Statement .
If the spring S1and S2 of force constant k1 and k2 respectively , are streached by the same force , it is found that more work is done on spring S1 then on spring S2
Statement -1: If statement by the same answer work done on S1 work on S1 is more then S2
Statement - 2 : k1<k2View SolutionTwo springs have their force constant as k1 and k2(k1>k2). When they are streched by the same force.
View SolutionTwo springs have their force constant as K1 and K2(K1<K2). When they are stretched by the same force:
View SolutionA 5 kg block in connected with two spring A and B having force constant, K1=200Nm and K2=300Nm respectively as shown in the figure . The block is released from rest with both the springs in natural length. The maximum energy stored in the spring A will be
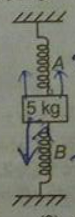 View Solution
View SolutionTwo identical massless springs A and B consist spring constant kA and kB respectively. Then :
View SolutionTwo similar springs P and Q have spring constant KP and KQ such that KP>KQ. They are stretched, first by the same amount (case a), then the same force (case b). The work done by the spring WP and WQ are related as, in case (b), respectively
View SolutionForce constant of two wires A and B of the same material are K and 2K respectively. If the two wires are stretched equally, then the ratio of work done in stretching (WAWB) is
View SolutionTwo bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1andk2 respectively. If the bodies Oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
View SolutionTwo particles (A) and (B) of equal masses are suspended from two massless spring of spring of spring constant k1 and k2, respectively, the ratio of amplitude of (A) and (B) is.
View SolutionTwo springs have spring constants k1andk2(k1≠k2). Both are extended by same force. If their elastic potential energical are U1andU2, then U1:U2 is
View Solution

