Two stars of masses m1andm2 are parts of a binary solar system. The radii of their orbits are r1andr2 respectively. The magnitude of the gravitational force m1 exerts on m2 is:Solution in Tamil
m1m2G(r1+r2)2
(m1+m2)(r1+r2)2
m1G(r1+r2)2
m2G(r1+r2)2
The correct Answer is:A

Separation between given stars of mass m1andm2=r1+r2
∴F1=Gm1m2(r1+r2)2
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (VERY SHORT ANSWER QUESTION)43videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (SHORT ANSWER QUESTIONS)28videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEXTBOOK QUESTION & ANSWERS (NUMERICAL PROBLEMS)30videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (V. Numerical problems).166videos
KINEMATICS
Similar Questions
Distinguish between the terms gravitation and gravity.
02:27View SolutionDefine 'G'. What are the units and dimensions of 'G' ?
02:03View SolutionAn unknown planet orbits the Sun with distance twice the semi major axis distance of the Earth's orbit. If the Earth's time period is T2, what is the time period of this unknown planet.
04:07View SolutionA crow is sitting on a branch of tree whose co-ordinates are (1,2,3) . A hunter is standing on the ground . Represent the position of the crow with respect to the hunter .
04:25View SolutionA system of binary stars of mass m_(A) and m_(B) are moving in circular orbits of radii r_(A) and r_(B) respectively. If T_(A) and T_(B) are at the time periods of masses m_(A) and m_(B) respectively then
08:19View SolutionTwo stars of mass m1 and m2 are parts of a binary star system. The radii of their orbits are r1 and r2 respectivey, measured from the centre of mass of the system. The magnitude of gravitational force m1 exerts on m2 is
01:51View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
02:50View SolutionTwo stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .02:10View SolutionA binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
02:10View Solutionm1 तथा m2 द्रव्यमान (m1>m2) के दो उपग्रह पृथ्वी के चारों ओर क्रमशः r2 तथा r2(r1>r2) त्रिज्याओं की वृत्तीय कक्षाओं में घूम रहे हैं । उनकी चाल v1 तथा v2 के विषय में कौन - सा कथन सत्य है -
04:01View SolutionTwo stars of masses m1andm2 are parts of a binary solar system. The radii of their orbits are r1andr2 respectively. The magnitude of the gravitational force m1 exerts on m2 is:
02:55View SolutionTwo satellites of masses m1andm2(m1>m2) are moving around the earth in orbits of radii r1andr2(r1>r2). Which one of the following statements about their velocities is correct?
02:00View SolutionTwo satellites of masses m1andm2(m1>m2) are moving around the earth in orbits of radii r1andr2(r1>r2). Which one of the following statements about their velocities is correct?
05:05View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
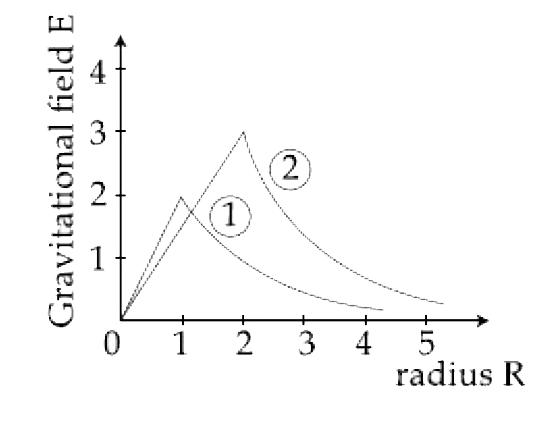 03:40View Solution
03:40View SolutionThe distance between two particles of masses m1andm2 is r. If the distance of these particles from the centre of mass of the system are r1andr2 respectively, then show that r1=r(m2m1+m2)andr2=r(m1m1+m2)
02:39View Solution

