Two tiny spheres carrying charges 1.5 µC and 2.5 µC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.Solution in Gujrati
Two charges 1.5 μC and 2.5 μC are placed at point A and B respectively. O is the mid point of the line joining two charges. The distance between these charges is 30 cm.
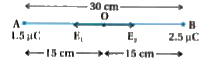
Electrical potential at point O.
Electrical potential at point O
VO=kq1r1+kq2r2
=k[1.5×10−60.15+2.5×10−60.15]
=9×109[4×10−60.15]
∴VO=2.4×105V
Electric field at point O .
EO=E2−E1=kq2r22−kq1r21
∴EO=k[q2qr22−q1r21]=9×109
[2.5×10−6(0.15)2−1.5×10−6(0.15)2]
∴EO=9×109×1.0×10−60.0225
∴EO=4×105Vm−1→ From 2.5μ C to 1.5μC
(b) Let P is on the perpendicular bisector from mid point of AB at a distance 10 cm .
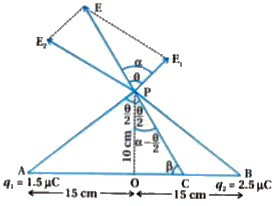
AP=BP = √152+102
=√325
= 18 cm = 0.18 m
Electric potential at point P
Vp=k[q1AP+q2BP]
=9×109[1.5×10−60.18+2.5×10−60.15]
=9×109×4×10−60.18
∴VP=2×105 V
Electric field at P due to q1
E1=kq1(AP)2=9×109×1.5×10−6(0.18)2
∴E1=0.42×106Vm−1 along AP
Electric field at P due to q2
E2=kq2(BP)2==9×109×2.5×10−6(0.18)2
∴E2=0.69×106Vm−1 along BP
Now ∠APO=∠BPO=θ2
and in ΔAOP
tanθ2=56.3∘
∴θ=112.6∘
Resultant electric field ,
E=√E21+E22+2E1E2cosθ
=
⎷(0.42×106)2+(0.69×106)2+2×0.42×0.69×1012×cos112.6∘
=[√0.1764+0.4761+0.2898×cos112.6∘]×106
=√0.6525+0.2898×(−0.3843)×106
∴E=√0.6525−0.2224×106
∴E=√0.4301×106
E=65559×106
∴E=6.6×106Vm−1
Suppose α is the angle made by E with E1
∴tanα=E2sinθE1+E2cosθ
=0.69×106sin112.6∘0.42×106+0.69×106cos112.6∘
[∵sin112.6∘=sin67.4∘]
=0.69×106×0.92390.42×106+0.69×106×(−0.3843)
=0.6375×1060.1548×106
∴tanα=4.1182
∴α=tan−14.1182
∴α=76.4∘
Suppose β is the angle made by E with BA
∴∠PCO=β
∴ In ΔPOC
β+α−θ2=90∘
∴β=90∘+θ2−α
∴β=90∘+112.6∘2−76.3∘
∴β=90∘+56.3∘−76.3∘
β=70∘
Hence, resultant electric field make an angle 70∘ to the line joining between charges 2.5μC to 1.5μC.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From DARPAN. Based on Textbook )
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B (questions)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B Numericals
16 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
An electric field is represented by →E=Axˆi where A = 10Vm2 . Find the potential of the origin with respect to the point (10,20) m.
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickless (12)d. Where d is the separation of the plates . How is the capacitance changed when the slab is inserted between the plates
View SolutionCalculate the potential at a point P due to a charge of 4×10−7 C located 9 cm away.
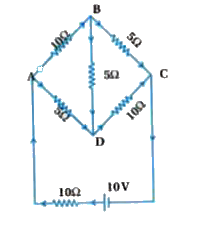
View SolutionDetermine the current in each branch of the given network.
View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionTwo tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionTwo tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View Solution1.5 μ C और 2.5μC आवेश वाले दो सूक्ष्म गोले 30 cm दूर स्थित हैं।
(a) दोनों आवेशों को मिलाने वाली रेखा के मध्य बिंदु पर, और
(b) मध्य बिंदु से होकर जाने वाली रेखा के अभिलम्ब तल में मध्य बिंदु से 10 cm दूर स्थित किसी बिंदु पर विभव और वैद्युत क्षेत्र ज्ञात कीजिए ।
View Solution1.5μC और 2.5μC आवेश वाले दो सूक्ष्म गोले 30 सेमी दूर स्थित है।
(a)दोनों आवेशों को मिलाने वाली रेखा के मध्य बिंदु पर, और
(b) मध्य बिंदु से होकर जाने वाली रेखा के अभिलम्ब तल में मध्य बिंदु से 10 सेमी दूर स्थित किसी बिंदु पर विभव or विद्युत क्षेत्र ज्ञात कीजिए।
View SolutionTwo tiny spheres carrying charges 1.8 muC and 2.8 mu C are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is
View SolutionTwo tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential and electric field :
(a) at the mid-point of the line joining the two charges and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
View SolutionTwo tiny spheres carrying charges 1.8 muC and 2.8 mu C are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is In the above question, the potential at a point20cm from the mid-point of the line joining the two charges in a place normal to the line and passing through the mid-point is
View SolutionTwo tiny spheres carrying charges 1.5μand2.5μC are located 30 cm apart. Find the potential and electric field.
a. at the mid-point of the line joining the two charges, and
b. at a point 10 cm from the midpoint in a plane normal to the line and passing through the mid-point.
View SolutionTwo tiny spheres carrying charges 1.5 µC and 2.5 µC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
View SolutionTwo tiny spheres carrying charges 1.5 µC and 2.5 µC are located 30 cm apart. Find the potential and electric field: (a) at the mid-point of the line joining the two charges, and (b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
View Solution
