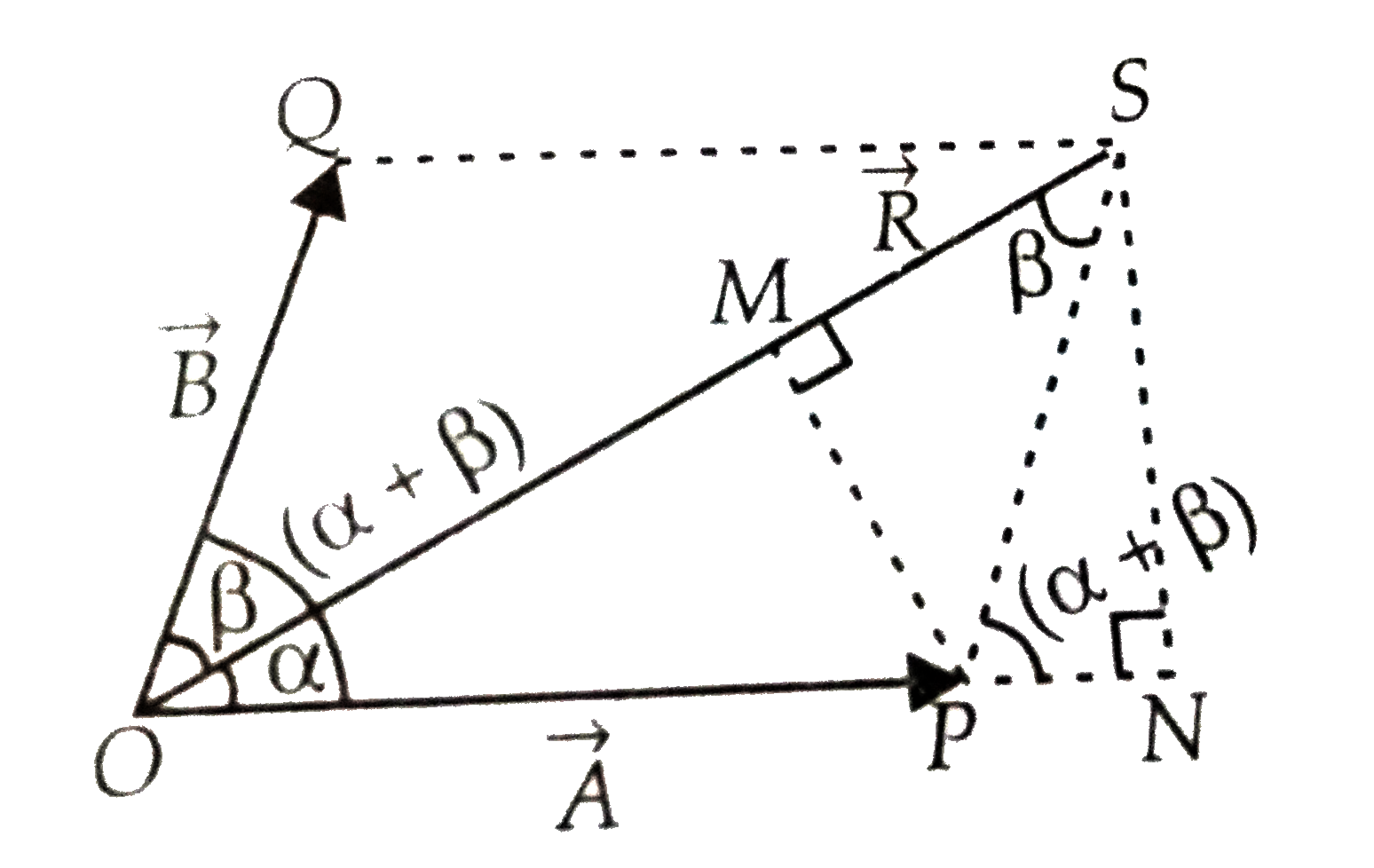
Two vectors $\to A and \to B$ inclined at an angle $θ$ have a resultant $\to R$ which makes an angle $α$ with $\to A$ and angle $β$ with $\to B$ . Let the magnitudes of the vectors $\to A, \to B and \to R$ be represented by A, B and R respectively. Which of the following relations is not correct ?

A

$\frac{R}{sin (α + β)} = \frac{A}{sin α} = \frac{B}{sin β}$

B

$R sin α = B sin (α + β)$

C

$A sin α = B sin β$

D

$R sin β = A sin (α + β)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $- - \to O P$ and $- - \to O Q$ represent two vectors $\to A and \to B$ making an angle $(α + β)$ . Using the parallelogram method of vector addition,
Resultant vector, $\to R = \to A + \to B$ SN is normal to OP and PM is normal to OS.
From the geometry of the figure,
$O S^{2} + O N^{2} + S N^{2} = {(O P + P N)}^{2} + S N^{2}$
$= {(A + B cos (α + β))}^{2} + {(B sin (α + β))}^{2}$
$R^{2} = A^{2} + B^{2} + 2 A B cos (α + β)$
In $△ O S N, S N = O S sin α = R sin α$
and in $△ P S N, S N + p S sin (α + β) = B sin (α + β)$
$∴ R sin α = B sin (α + β) or \frac{R}{sin (α + β)} = \frac{B}{sin α} ... (i)$
Similary, PM $= A sin α + B sin β$
$\frac{A}{sin β} = \frac{B}{sin α} ... (i i)$
Combining (i) and (ii), we get
$\frac{R}{sin (α + β)} = \frac{A}{sin β} = \frac{B}{sin α} ... (i i i)$
From eqn. (iii), $R sin β = A sin (α + β)$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The resultant of $\to A$ and $\to B$ makes an angle $α$ with $\to A and \to β$ with $\to B$ , then -
A $α < β$
B $α < β if A < B$
C $α < β if A > B$
D $α < β if A = B$
Question 2 - Select One
The resultant of $\to A and \to B$ makes an angle alpha with $\to A$ and $β and \to B$ ,
A $α < β$
B $α < β if A < B$
C $α < β if A < β$
D $α < b e t if A = B .$
Question 3 - Select One
If the resultant of $\to A$ and $\to B$ makes angle $α$ with $\to A$ and $β$ with $\to B$ , then
A $α < β$ always
B $α < β$ if $A < B$
C $α < β$ if $A > B$
D $α < β$ if A=B

NCERT FINGERTIPS-MOTION IN A PLANE -Vector Addition - Analytical Method

Home
Ask Doubt
Profile