Two wires A and B of same dimensions are stretched by same amount of force .Young's modulus of A is twice that of B. Which wire will get more elongation?
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the elongation of the two wires A and B when they are subjected to the same force. We will use the formula for elongation based on Young's modulus.
1. Understanding the Problem:
- We have two wires, A and B, with the same dimensions (same length and cross-sectional area).
- The Young's modulus of wire A (E1) is twice that of wire B (E2). Therefore, we can express this as:
E1=2E2
2. Formula for Elongation:
- The elongation (ΔL) of a wire when a force (F) is applied can be calculated using the formula:
ΔL=F⋅LA⋅E
- Where:
- F = applied force
- L = original length of the wire
- A = cross-sectional area
- E = Young's modulus of the material
3. Calculating Elongation for Wire A:
- For wire A, the elongation (ΔL1) can be expressed as:
ΔL1=F⋅LA⋅E1
4. Calculating Elongation for Wire B:
- For wire B, the elongation (ΔL2) can be expressed as:
ΔL2=F⋅LA⋅E2
5. Finding the Ratio of Elongations:
- To compare the elongations, we can take the ratio of ΔL1 to ΔL2:
ΔL1ΔL2=F⋅LA⋅E1F⋅LA⋅E2=E2E1
- Since E1=2E2, we can substitute this into the equation:
ΔL1ΔL2=E22E2=12
6. Conclusion:
- From the ratio, we find that:
ΔL2=2ΔL1
- This means that the elongation of wire B (ΔL2) is twice that of wire A (ΔL1). Therefore, wire B will experience more elongation than wire A.
Final Answer:
Wire B will get more elongated.
- We have two wires, A and B, with the same dimensions (same length and cross-sectional area).
- The Young's modulus of wire A (E1) is twice that of wire B (E2). Therefore, we can express this as:
E1=2E2
- The elongation (ΔL) of a wire when a force (F) is applied can be calculated using the formula:
ΔL=F⋅LA⋅E
- Where:
- F = applied force
- L = original length of the wire
- A = cross-sectional area
- E = Young's modulus of the material
- For wire A, the elongation (ΔL1) can be expressed as:
ΔL1=F⋅LA⋅E1
- For wire B, the elongation (ΔL2) can be expressed as:
ΔL2=F⋅LA⋅E2
- To compare the elongations, we can take the ratio of ΔL1 to ΔL2:
ΔL1ΔL2=F⋅LA⋅E1F⋅LA⋅E2=E2E1
- Since E1=2E2, we can substitute this into the equation:
ΔL1ΔL2=E22E2=12
- From the ratio, we find that:
ΔL2=2ΔL1
- This means that the elongation of wire B (ΔL2) is twice that of wire A (ΔL1). Therefore, wire B will experience more elongation than wire A.
Wire B will get more elongated.
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Exercise 15.2
2 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Assertion And Reason
22 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - MiscellaneousExamples
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Two wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionTwo wires P and Q are equally thick and made of the same material but the length of Pis twice that of Q
(a) Which wire will have a greater extension for a given load ?
(b) Which one will undergo a greater strain ?
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a width mg, fig. What is the net elongation in the two wires?
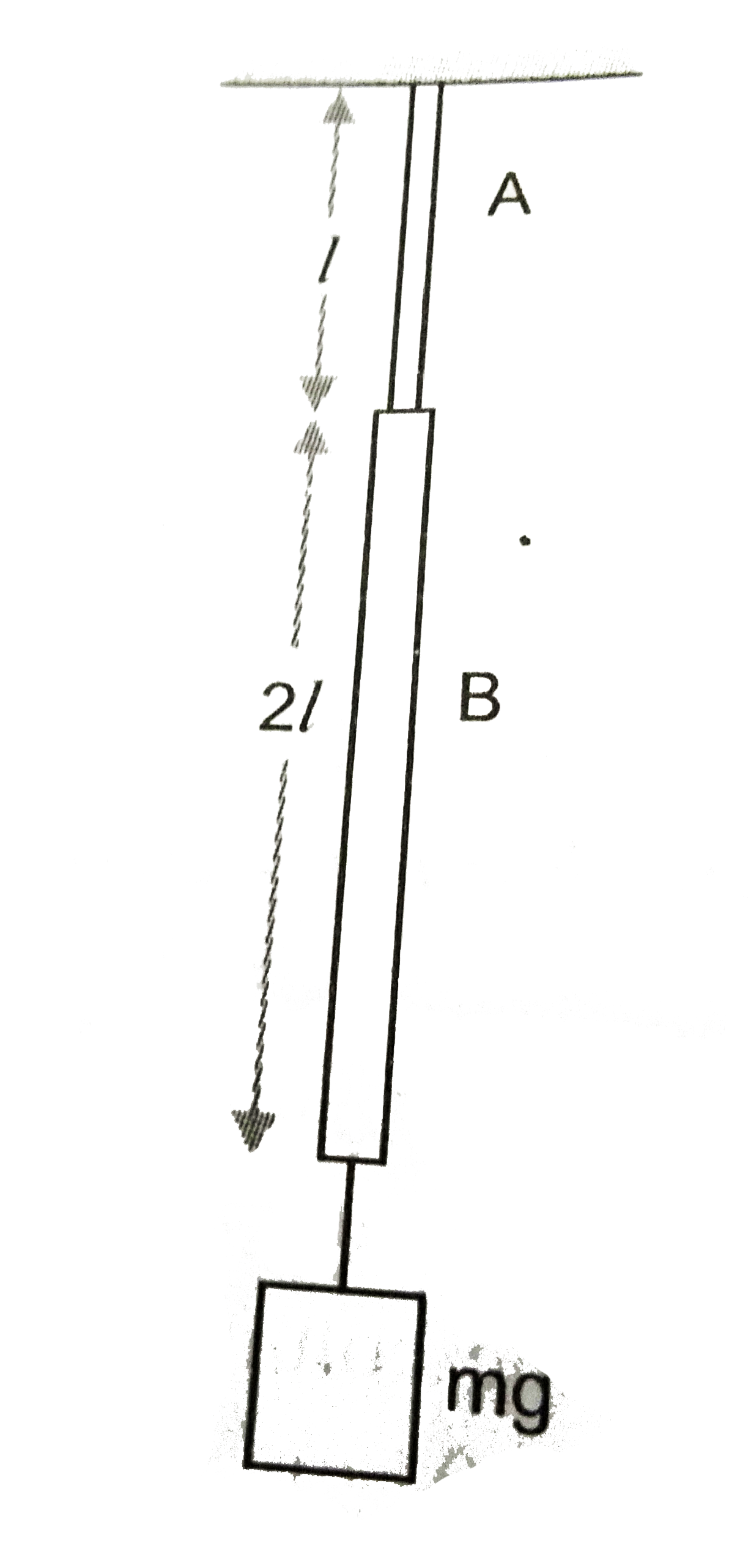
View SolutionTwo wires A and B have equal lengths and aremade of the same material , but diameter of wire A is twice that of wire B. Then, for a given load,
View SolutionTwo metal wires P and Q of same length and material are stretched by same load. Yheir masses are in the ratio m1:m2. The ratio of elongation of wire P to that of Q is
View SolutionTwo wires of the same material and same mass are stretched by the same force. Their lengths are in the ratio 2:3. Their elongation are in the ratio
View SolutionTwo wires of equal length are stretched by the same force. One wire is heavy while the other is light which one will have less frequency
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View Solution
