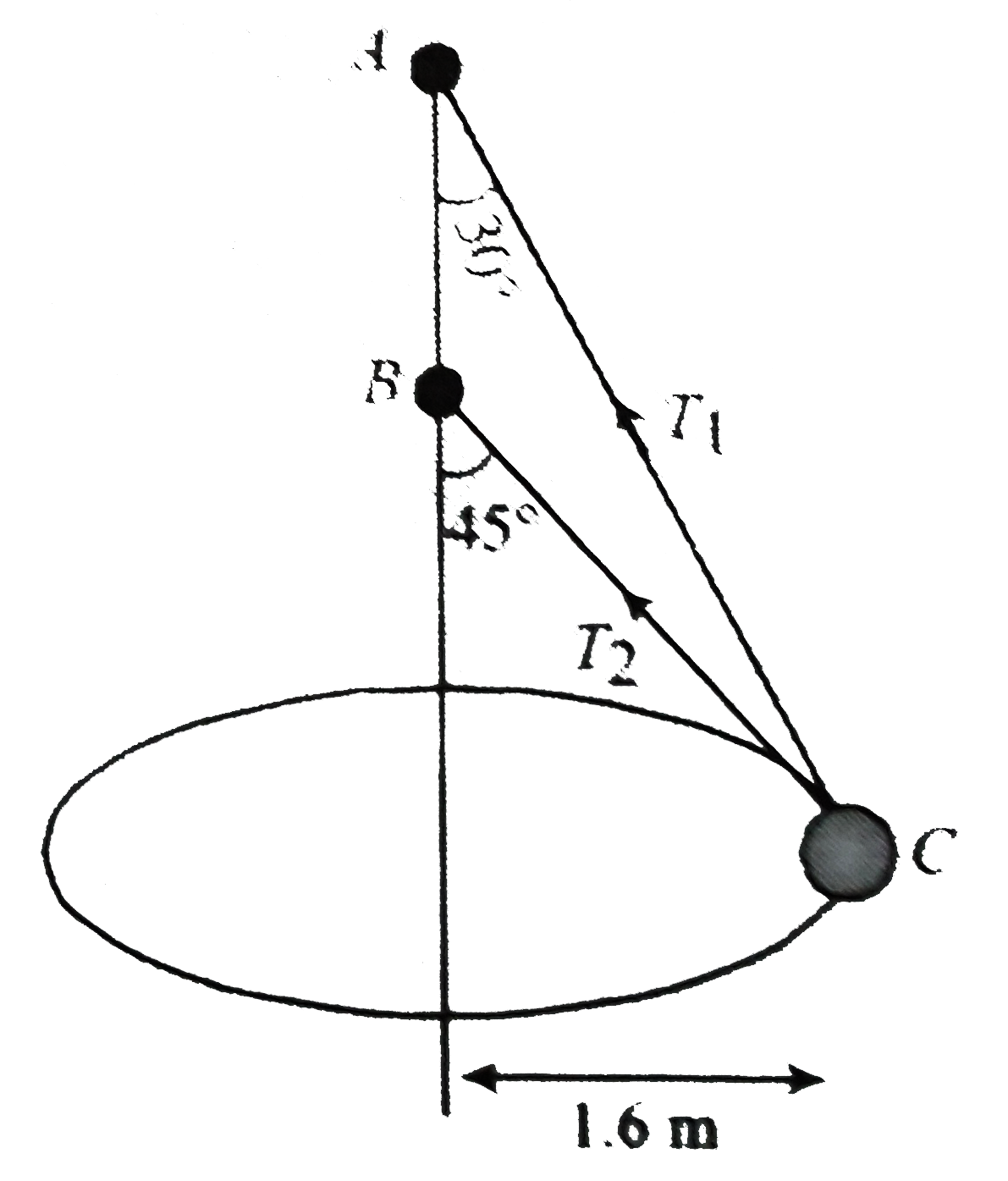
Two wires Ac an Bc are tied at C of small sphere of mass 5 kg Which reolves at ta constant speed v in the horzontal circle of radius of 1.6 m. The minimum value of v is

3.01m/s
4.01m/s
8.2m/s
3.96m/s
(d) From the figure
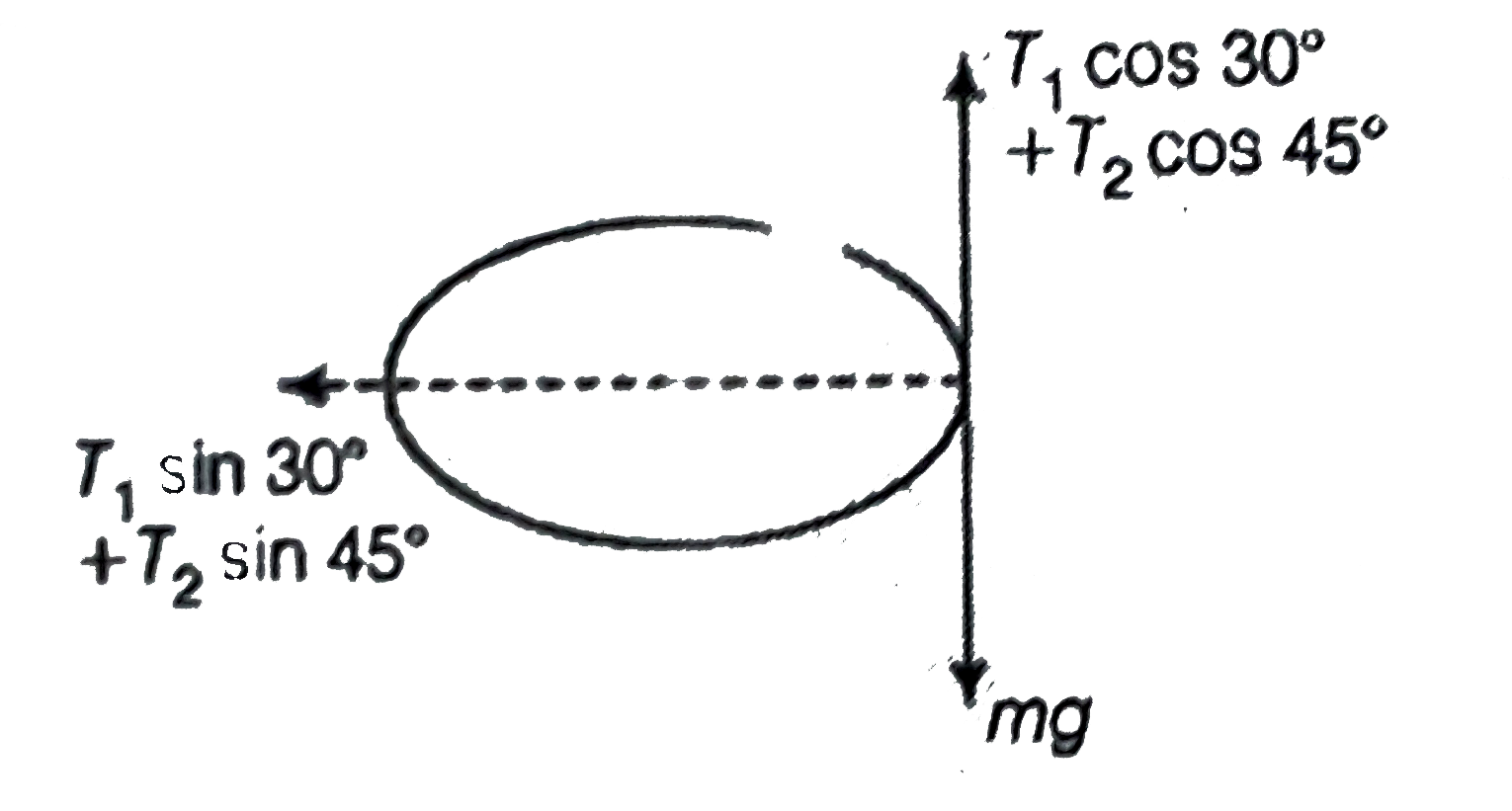
T1cos30∘+T2cos45∘=mg
and T1sin30∘+T2sin45∘=mv2r
From Eq. (i) and Eq. (ii) we get T1=mg−mv2r(√(3)−12)
But, T1−≥o
T1=mg−mv2r(√(3)−12)≥0
mg≥mv2r⇒v≤√rg
vmax=r√rg=√1.6×9.8=3.96m/s
Topper's Solved these Questions
Similar Questions
Two wires ACandBC are tied at C of small sphere of mass 5kg which revolves at a constant speed v in the horizontal circle of radius 1.6m Find the maximum value of v
 View Solution
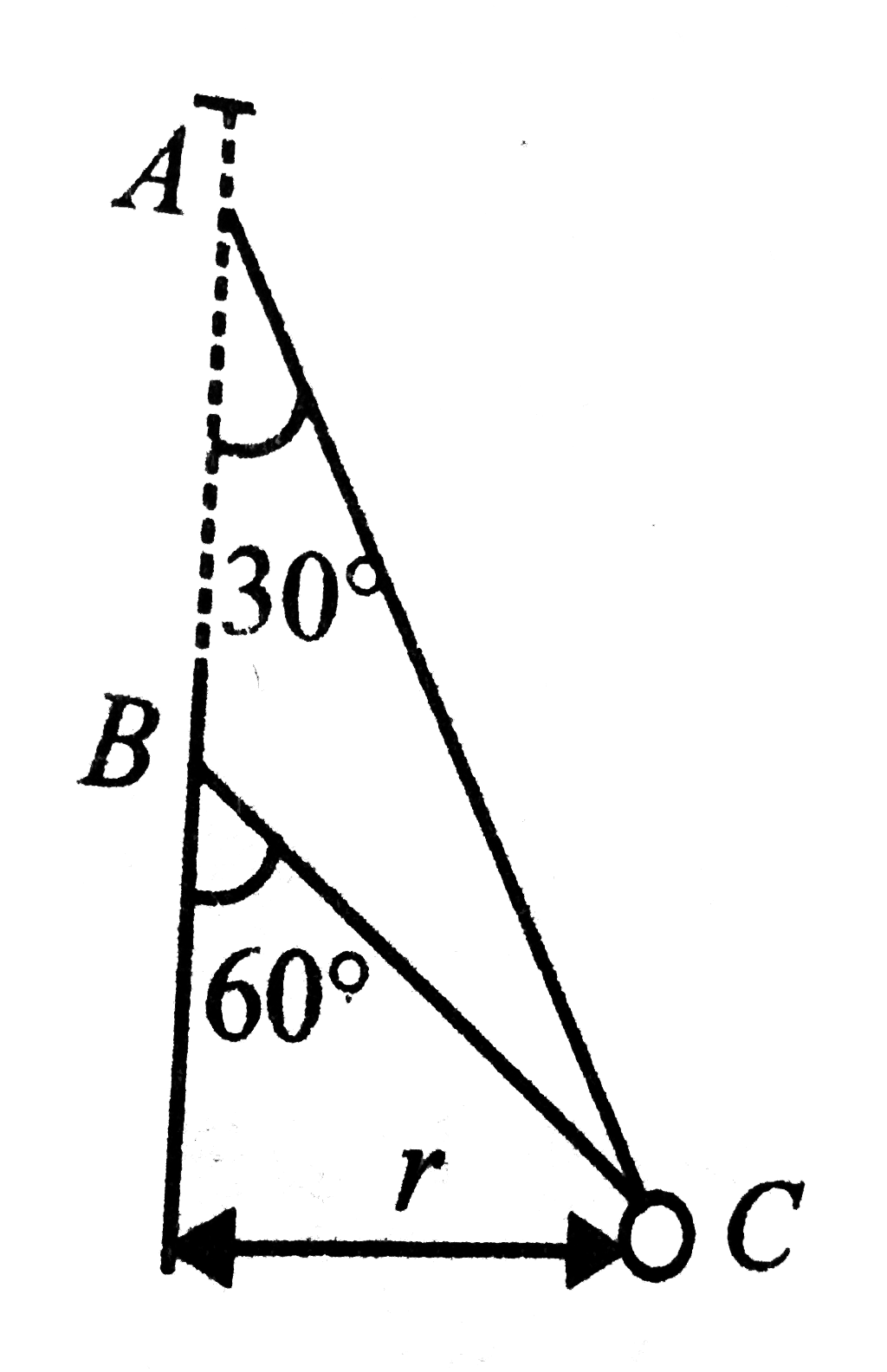
View SolutionA single wire ACB passes through a smooth ring at C when revolves at a constant speed in the horizontal circle of radius r=6.4m as shown in the figure. Find the speed (in m/s) of revolution of the ring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
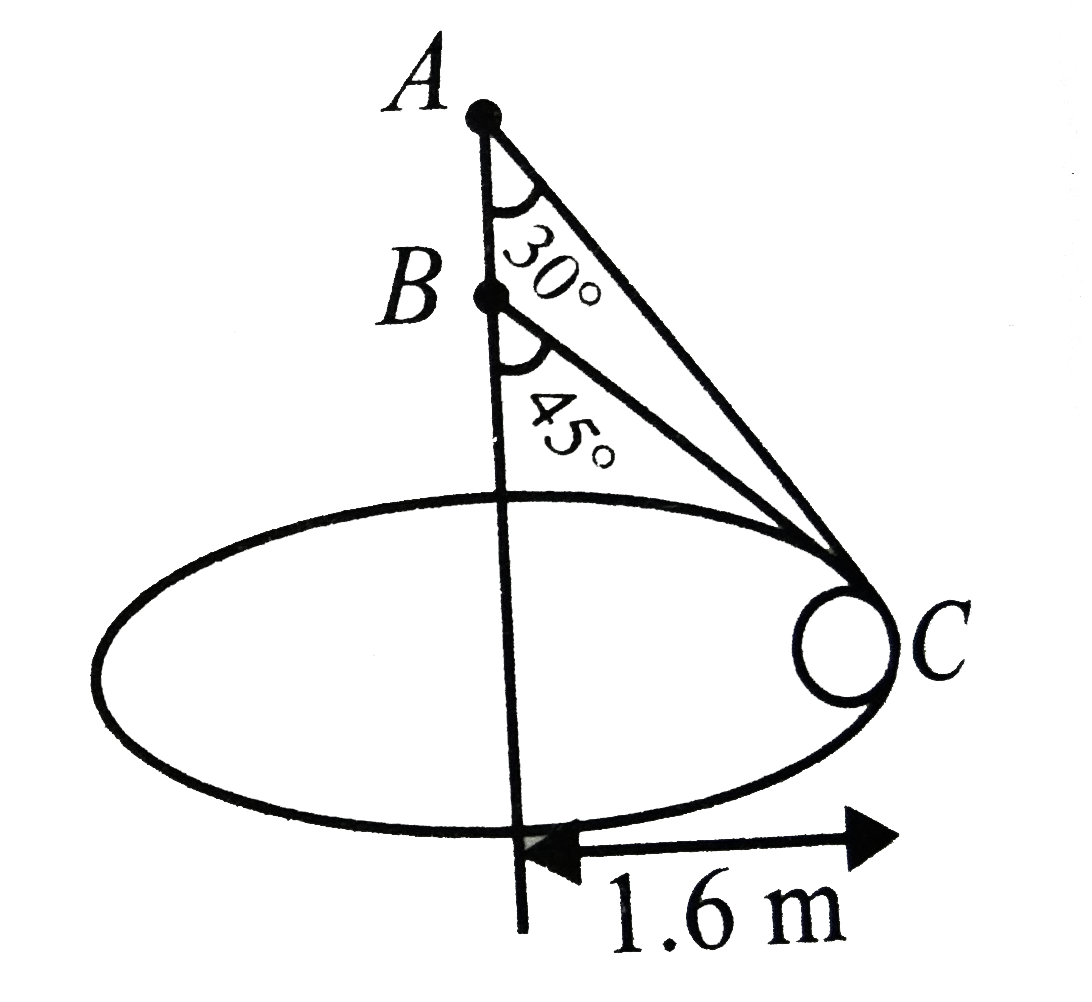
Two wires AC and BC are tied at C of a small sphere of mass 5kg, wheich revolves at a constant speed v in the horizontal speed v in the horizontal circle of radius 1.6m. Find the minimum value of v
 A4ms−1B2ms−1C2.5ms−1Dnone of these
A4ms−1B2ms−1C2.5ms−1Dnone of these - Question 2 - Select One
A single wire ACB passes through a smooth ring at C which revolves at a constant speed in the horizontal circle of radius r as shown in the fig. the speed of revolution is
 A√rgB√2rgC2√2rgD2√rg
A√rgB√2rgC2√2rgD2√rg - Question 3 - Select One
A body of mass 10 kg moves with a constant speed v of 2 ms−1 along a circular path of radius 8 m. The power produced by the body will be
A10 Js−1B98 Js−1C49 Js−1Dzero
The breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 View Solution
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA stone of mass m tied to a string of length l rotates along circumference of a circle with constant speed v. The torque on the stone is
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View Solution

