Ultraviolet radiations of wavelengths 800 Å and 700 Å when allowed to fall on Hydrogen atoms in their ground state, were found to liberate electrons with maximum kinetic energies 1.96 eV and 4.18 eV respectively. Calculate Planck,s constant and work function or ionisation energy of the hydrogen atom. Solution in Kannada
λ1=8×10−8m,λ2=7×10−8m
k1=1.96×1.6×10−19J=3.136×10−19J
k2=4.18×1.6×10−19J=6.688×10−19J
We know that E=w+(KE)max
i.e., hv1=w+k1
hv2−w+k2
∴(k2−k1)=h(v2−v1)
i.e., h=(k2−k1)c(1λ2−1λ1)
or h=(k2−k1)(λ1λ2)c(λ2−λ1)=(6.688−3.136)10−19×8×7×10−163×108(8−7)10−8
Planck.s constant h=6.630x10−34Js.
Work function, =(6.630×10−34×3×1088×10−8)−(3.136×1019)
=24.86×10−19−3.136×10−19
=21.724×10−19J÷1.6×10−19=13.58eV
i.e., Ionisation energy =13.58 eV.
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - FIVE MARK QUESTIONS WITH ANSWERS5videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - SUBHASH PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - NUMERICAL PROBLEMS AND ANSWERS29videos
CURRENT ELECTRICITY
- BOOK - SUBHASH PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NUMERICALS WITH SOLUTIONS21videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
Write any three experimental observations of photoelectric effect
04:15View SolutionIn the given circuit, calculate the effective resistance between A and B.
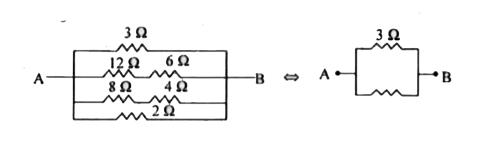 02:09View Solution
02:09View SolutionTwo point charges −2nC and +8nC are separated in air by a distance of 0.10m.Find the position of the neutral point along the line joining the 2 point charges.
03:47View SolutionUltraviolet light of wavelength 800 A and 700 A when allowed to fall on hydrogen atoms in their ground states is found to liberate electrons with kinetic energies 1.8eV and 4.0eV , respectively. Find the value of Planck's constant.
03:31View SolutionThe ionisation energy of hydrogen atom is 13.6 eV. Calculate Rydberg's constant for hydrogen.
01:37View SolutionU.V. light of wavelength 800A∘&700A∘ falls on hydrogen atoms in their ground state & liberates electrons with kinetic energy 1.8eV and 4eV respectively. Calculate planck's constant.
05:22View SolutionUltraviolet light of wavelengths lambda_(1) and lambda_(2) when allowed to fall on hydrogen atoms in their ground state is found to liberate electrons with kinetic energy 1.8 eV and 4.0 eV respectively. Find the value of (lambda_(1))/(lambda_(2)) .
05:58View SolutionThe ground state energy of hydrogen atom is-13.6 eV. What are the kinetic and potential energies of the electron in this state ?
04:05View Solutionहाइड्रोजन परमाणु की निम्नतम अवस्था में 500 Å तथा 600 Å तरंगदैर्घ्य का प्रकाश डाला जाता है , तो हाइड्रोजन परमाणु से क्रमशः 6.2 eV तथा 2.2 eV गतिज ऊर्जा वाले इलेक्ट्रॉनों का निष्कासन होता है । प्लांक नियतांक का मान ज्ञात कीजिए ।
10:13View SolutionThe threshold wavelenght of silver is 3800Å . Calculate the maximum kinetic energy in eV of photoelelctrons emitted, when ultraviolet light of wavelegth 2600Å falls on it. ( Planck's constant, h=6⋅63×10−34Js,. Velocity of light in air, c=3×108m/s)
03:26View SolutionUltraviolet rays of wavelengths 800Å and 700Å fall on a hydrogen atom initially in its minimum energy state. As a result, electrons having energies 1.8 eV and 4.0 eV are emitted. Determine the value of Planck's constant
02:53View SolutionWhen ultraviolet light of 800 Å and 700 Å wavelengths is incident on a hydrogen atom located at the surface, it emits electrons with kinetic energy of 1.8eV and 4.0eV, respectively. What is the value of Planck constant?
01:37View Solutionहाइड्रोजन परमाणुओं पर उनकी निम्नतम अवस्था में 800Å और 700Å तरंगदैर्ध्य का पराबैंगनी प्रकाश जब पड़ने दिया जाता है, तो यह क्रमशः 1.8 eV और 4.0 eV गतिज ऊर्जा के इलेक्ट्रॉन मुक्त करता पाया जाता है। प्लान्क स्थिरता निकालें।
01:33View SolutionThe energy of the electron in the ground state of hydrogen atom is −13.6eV. Find the kinetic energy and potential energy of electron in this state.
01:24View SolutionThe energy of the electron in the ground state of hydrogen atom is −13.6eV. Find the kinetic energy and potential energy of electron in this state.
05:02View Solution

