Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The angle α between the particle's velocity vector and y-axis at and moment is
The correct Answer is:[(a) 2π2n2mE/qB2; (b) tan−1(Bv02πEn)]
Step by step video, text & image solution for Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q//m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v_0 The angle alpha between the particle's velocity vector and y-axis at and moment is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - Advance MCQ
29 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
- NUCLEAR PHYSICS AND RADIOACTIVITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NUCLEAR PHYSICS AND RADIOACTIVITYEXERCISE - Concptual MCQs
48 Videos
Similar Questions
Uniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.

The angle α between the particle’s velocity vector and y-axis at that moment is:
View SolutionUnifrom electric and magnetic fields with strength E and induction B respectively are directed along the y axis (Fig). A particle with specific charge q/m leaves the origin O in the direction of the z axis with an initial non-realtive velocity v0 find:
(a) the coordinate yn of the particle when it crossses then y axis for the nth time,
(b) the angle α between the particle's velocity vector and the y axis at that moment.

View Solution
Knowledge Check
Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate y_nofthepartic≤whenitcrossesthey−aξsforthen^(th) time isA2π2mn2EqB2Bπ2mn2EqB2C2π2mn2E3qB2D√3π2mn2EqB2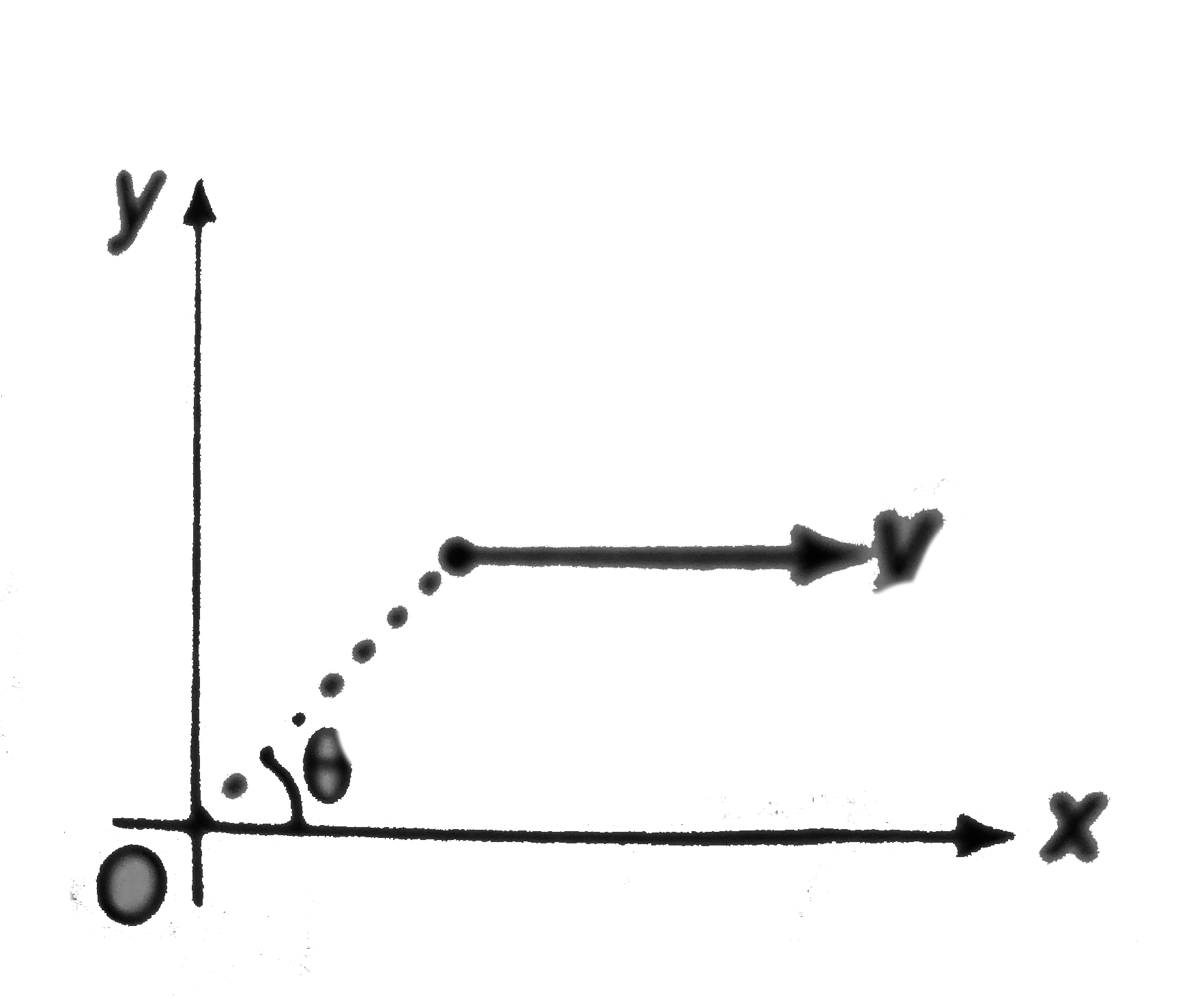
A particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin OAremains constantBcontinuously increasesCcontinuously decreasesDoscillates.A particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.
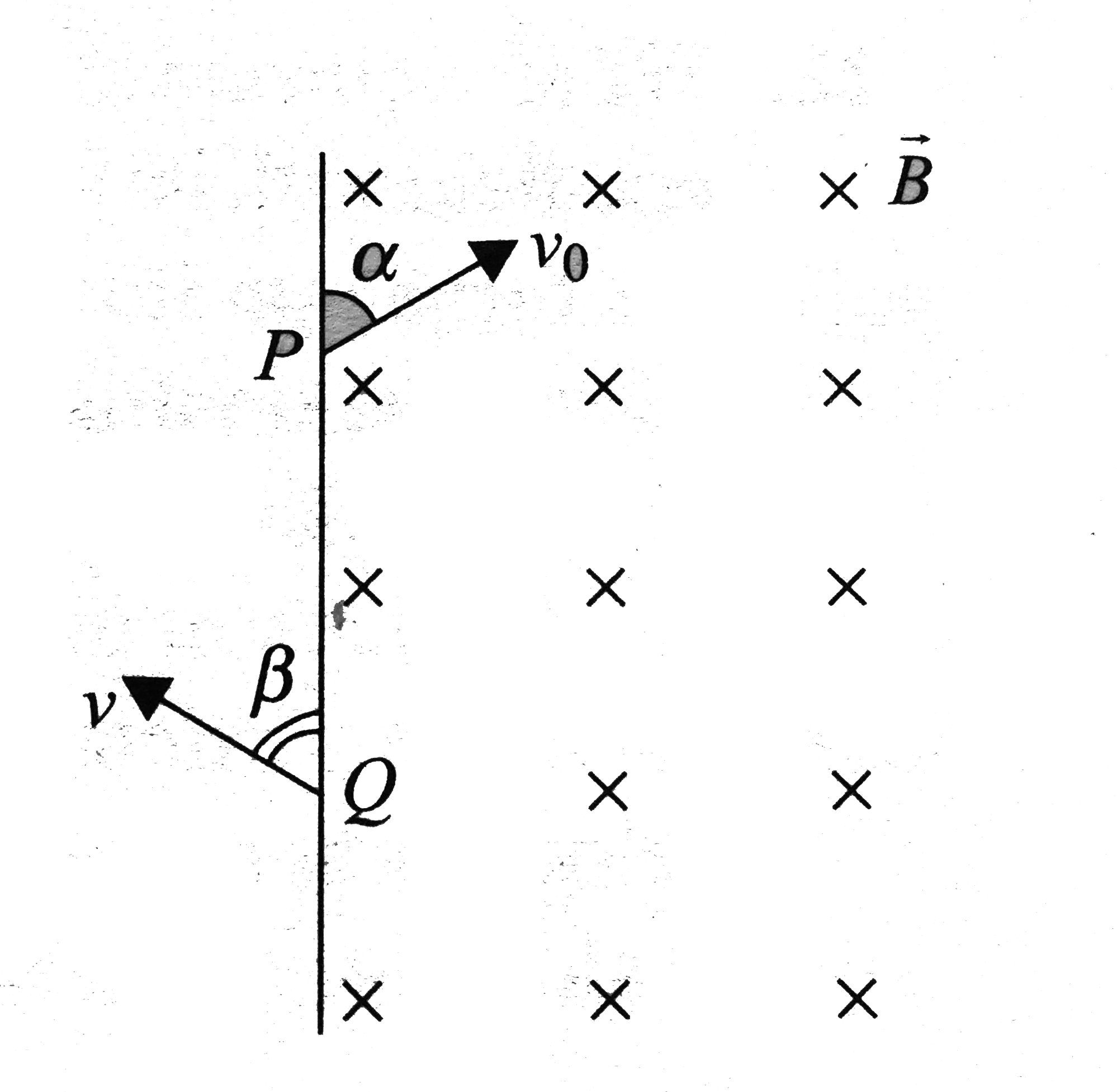 Aα=βBv=v0CPQ=2mv0sinαBqDThe particle remains in field for time t=2m(π−α)Bq
Aα=βBv=v0CPQ=2mv0sinαBqDThe particle remains in field for time t=2m(π−α)Bq
Uniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge qm leves the origin in the direction of x-axis with an initial velocity v0. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle α between the particle's velocity vector adn the y-axis for nth time
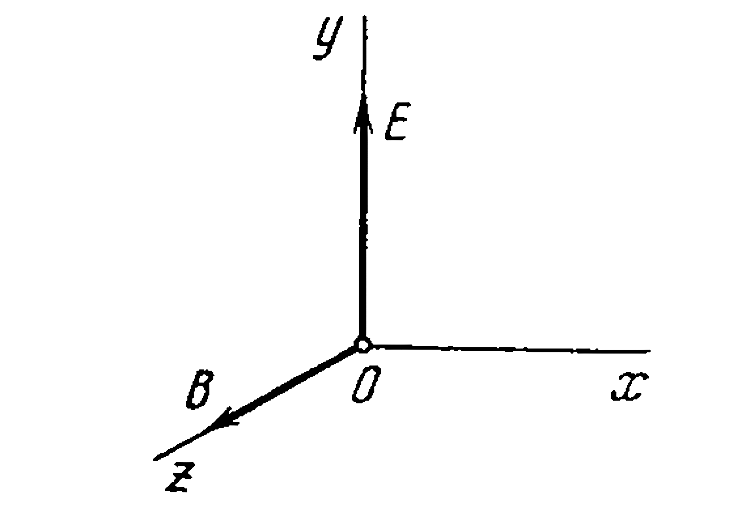
View SolutionA particle with specific charge q/m moves in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with strength E and induction B (fig). At the moment t=0 the particle was located at the point O and had zero velocity. For the non-relativistic case find:
(a) the law of motion x(f) and y(t) of the particle, the shape of the trajectory,
(b) the lenght of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero,
(c) the mean value of the particle's velocity vector projections on the x axis (the drift velocity).
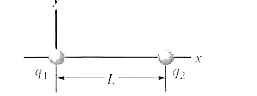
View SolutionTwo charged particles lie along x axis as shown in Fig. The particle with charge q2=+8μC is at x = 6.00 m, and the particle with charge q1=+2μC is at the origin. Locate the point where the resultant electric field is zero.
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionAssertion: Uniform electric and magnetic field are applied along Y-axis andZ-axis respectively. Kinetic energy of particle released at rest from origin depends only on the y-coordinate of particle.
Reason: Work done by the magnetic force is zero. Kinetic energy gained by the particle is only due to electric force
View Solution