Unstable pions are produced as a beam in a nuclear reaction experiment . The pions leave the target at a speed of 0.995c. The intensity of the beam reduces to half its original value as the beam travels a distance of 39 m . Find the half - life of pions (a) in the laboratory frame, (b) in their rest frame.
To solve the problem step by step, we will break it down into two parts: (a) finding the half-life of pions in the laboratory frame and (b) finding the half-life in their rest frame.
Part (a): Half-life in the Laboratory Frame
1. Identify the given values:
- Speed of pions, v=0.995c
- Distance traveled, d=39m
- Speed of light, c=3×108m/s
2. Calculate the time taken to travel the distance:
- The time t taken to travel a distance d at speed v is given by:
t=dv
- Substitute the values:
t=39m0.995×3×108m/s
3. Calculate the value:
- First, calculate 0.995×3×108:
0.995×3×108≈2.985×108m/s
- Now, calculate t:
t=392.985×108≈1.3×10−7s
4. Conclusion for part (a):
- The half-life of pions in the laboratory frame is:
thalf=1.3×10−7s
Part (b): Half-life in the Rest Frame
1. Use the time dilation formula:
- The relationship between the half-life in the laboratory frame thalf and the proper half-life t′half in the rest frame is given by:
t′half=thalf√1−v2c2
2. Calculate v2c2:
- Given v=0.995c:
v2c2=(0.995)2≈0.990025
- Therefore:
1−v2c2≈1−0.990025≈0.009975
3. Calculate the square root:
- Now take the square root:
√1−v2c2≈√0.009975≈0.099875
4. Calculate t′half:
- Substitute thalf and the square root into the formula:
t′half=1.3×10−7s×0.099875≈1.299×10−8s
5. Conclusion for part (b):
- The half-life of pions in their rest frame is:
t′half≈1.3×10−8s
Final Answers:
- (a) Half-life in the laboratory frame: thalf=1.3×10−7s
- (b) Half-life in the rest frame: t′half≈1.3×10−8s
- Speed of pions, v=0.995c
- Distance traveled, d=39m
- Speed of light, c=3×108m/s
- The time t taken to travel a distance d at speed v is given by:
t=dv
- Substitute the values:
t=39m0.995×3×108m/s
- First, calculate 0.995×3×108:
0.995×3×108≈2.985×108m/s
- Now, calculate t:
t=392.985×108≈1.3×10−7s
- The half-life of pions in the laboratory frame is:
thalf=1.3×10−7s
- The relationship between the half-life in the laboratory frame thalf and the proper half-life t′half in the rest frame is given by:
t′half=thalf√1−v2c2
- Given v=0.995c:
v2c2=(0.995)2≈0.990025
- Therefore:
1−v2c2≈1−0.990025≈0.009975
- Now take the square root:
√1−v2c2≈√0.009975≈0.099875
- Substitute thalf and the square root into the formula:
t′half=1.3×10−7s×0.099875≈1.299×10−8s
- The half-life of pions in their rest frame is:
t′half≈1.3×10−8s
- (a) Half-life in the laboratory frame: thalf=1.3×10−7s
- (b) Half-life in the rest frame: t′half≈1.3×10−8s
Topper's Solved these Questions
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective
2 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective 2
1 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer
2 Videos
- THE NUCLEOUSBOOK - HC VERMA ENGLISHCHAPTER - THE NUCLEOUSEXERCISE - Short answer
12 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Short Question
9 Videos
Similar Questions
An accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The total energy (E) of a proton in the beam travelling with seed v at a distance of r(r≥R) from point O. Assuming that the sphere has acquired an electrostatic charge Q is
View SolutionA train starts from rest and moves with a constant accelerationof 2.0ms2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find a. the total distance moved by the train, b. the maximum speed attained by the train and c. the position(s) of the train at half the maximum speed.
View SolutionMonochromatic light of wavelength 632.8nm is produced by a helium-neon laser. The power emitted is 9.42mW. (a) Find the energy and momentum of each photon in the light beam. (b) How many photons per second, on the average, arrive at a target irradiated by this beam? (Assume the beam to have uniform cross-section which is less than the target area). (c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon. h=6.663×10−34Js,1a.m.u.=1.66×10−27kg.
View SolutionTwo neutron stars are separated by a distance of 1010m. They each have a mass of 1030kg and a radius of 105m. They are initially at rest with respect to each other.
As measured from the rest frame, how fast are they moving when
(a) their separation has decreaed to one - half its initial value,
(b) they are about to collide .
View Solution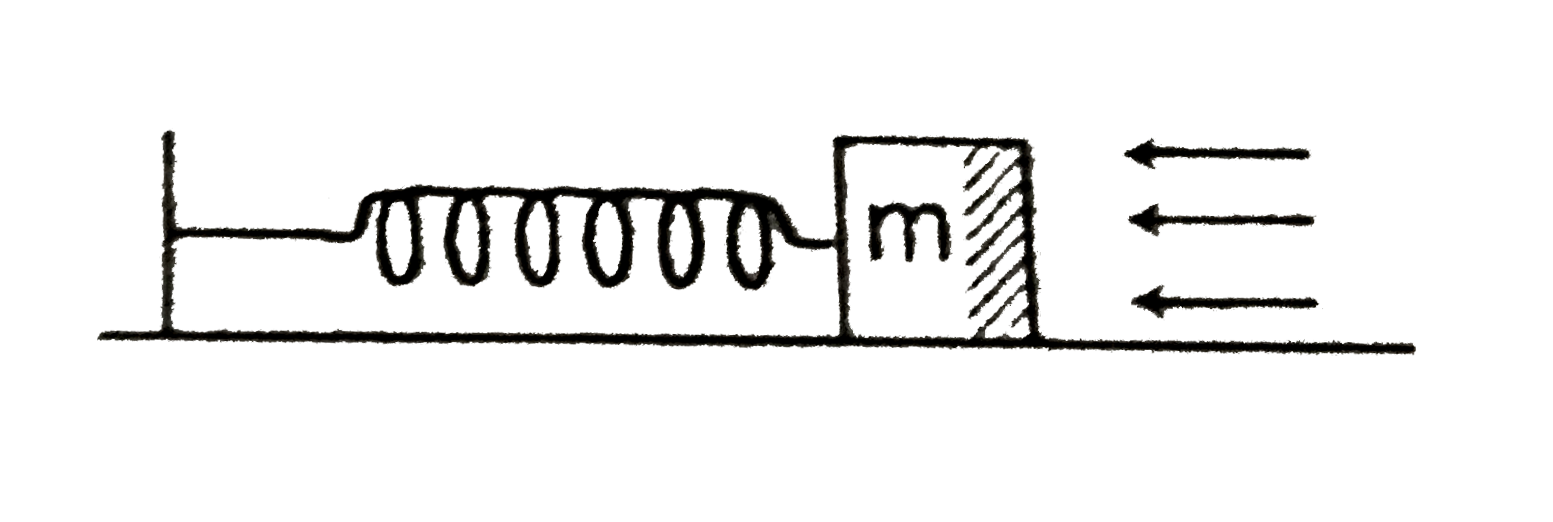
A spring block system with mass of block m and spring constant K (all the surfaces of blocks are perfectly abosrbing and smooth) is placed on a smooth horizontal plane as shown in the diagram at rest. A light beam of intensity l is switched on its right side. find the amplitude of oscillations of the block. (face area of block is A and c is the speed of light in vacuum)
View SolutionState the following statements as TRUE or FALSE.
a. A convex mirror cannot from a real image for a real object.
b. The image formed by a convex mirror is always diminished and erect.
c. Virtual image formed by a concave mirror is always enlarged.
d. Only in the case of a concave mirror, it may happen that the object and its image move in same direction.
e. In the case of a concave mirror, the image always move faster than the object.
f. If an object is placed in front of a diverging mirror at a distance equal to its focal length, then the height of image formed is half of the height of object.
g. For two positions of an object , a concave mirror can form englarged image.
h. Concave mirror is used as a rear view mirror in motor vehicles.
i. If some portion of the mirror ois covered, then complete image will be formed but of reduced brightness.
j. A plane mirror always forms an erect iamge of same size as that of the object.
k. The image formed by a plane mirror has left-right reversal.
l. A virtual object means a converging beam.
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
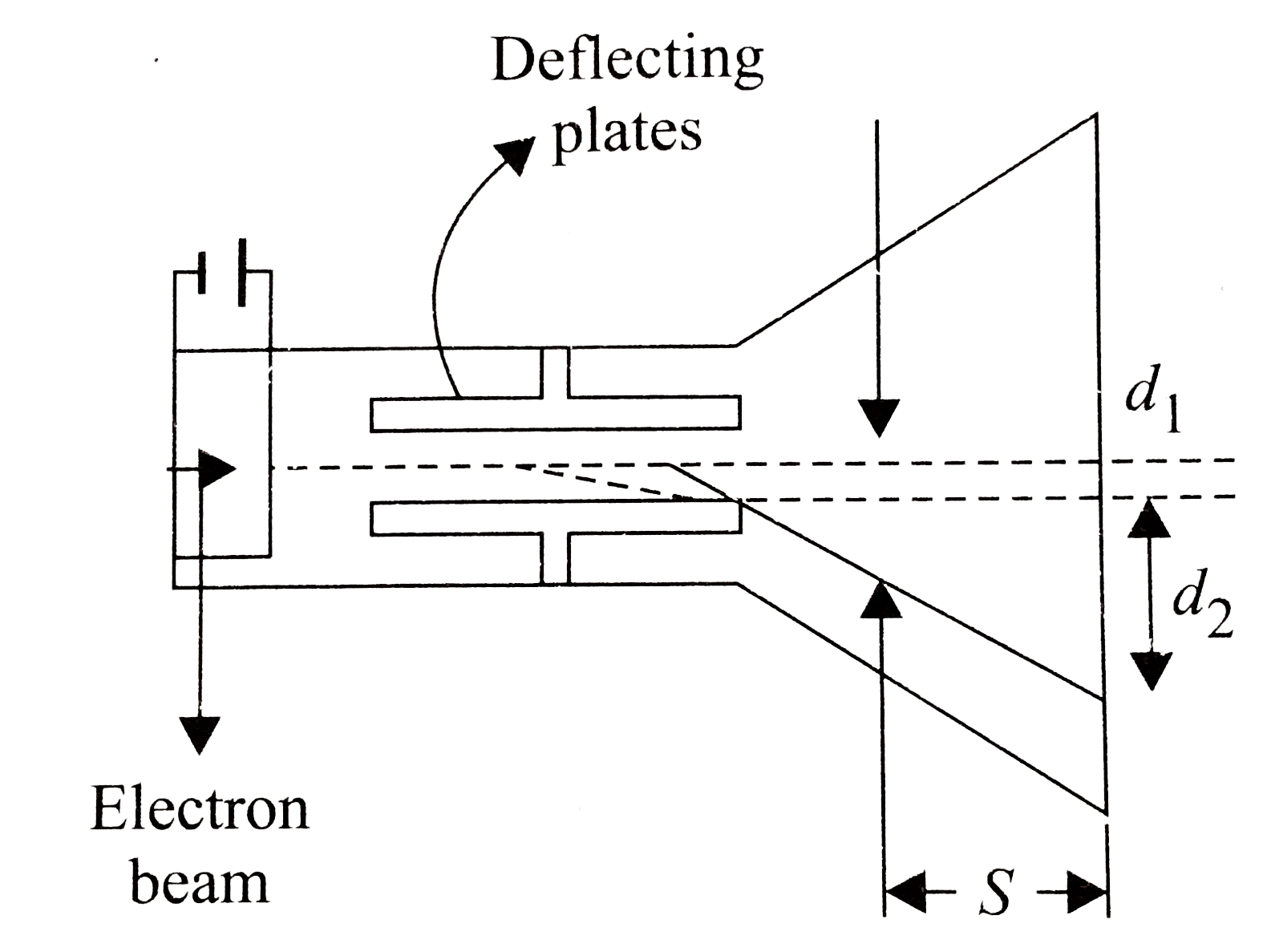
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
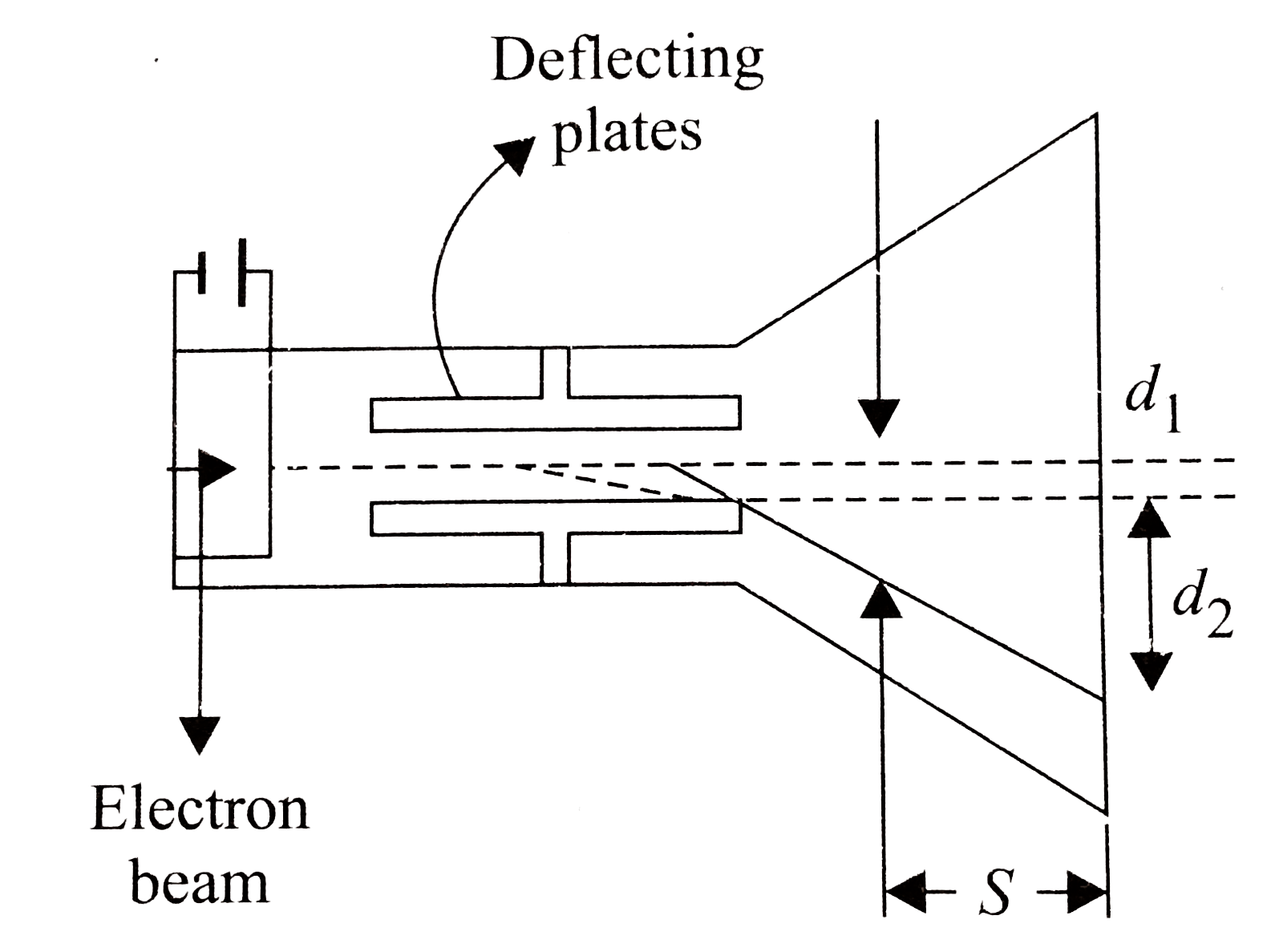
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment
View SolutionIn figure S is a monochromatic point source emitting light of wavelength λ=500nm. A thin lens of circular shape and focal length 0.10m is cut into two identical halves L1 and L2 by a plane passing through a doameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5mm. The distance along the axis from A to L1 and L2 is 0.15m, while that from L1 and L2 to O is 1.30m. The screen at O is normal to SO.
(a) If the 3rd intensity maximum occurs at point P on screen, find distance OP.
(b) If the gap between L1 and L2 is reduced from its original value of 0.5mm, will the distance OP increases, devreases or remain the same?

View Solution
