Question

Upside down racing: A modern race car is designed so that the passing air pushes down on it, allowing the car to travel much faster through a flat turn in a Grand Prix without friction failing. This downward push is called negative lift. Can a race can have so muchh negative lift it could be driven upside won on a long ceiling, as done fictionally by a sedan in the first Men in Black movie?
Figure represents a Grand Prix race car of mass m=600 kg as it travels on a flat in a circular arc of radius R=100m. Becuase of the shape of the car and the wings on it, passing air exerts a negative lift ${\overrightarrow{F}}_L$

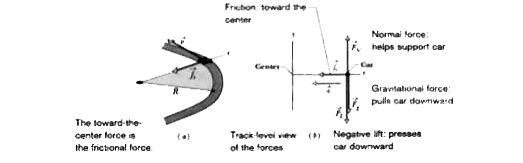
downward on the car. The coefficient of static friction between the tires and the track is 0.75. (Assume that the forces on the four tires are identical).
a. If the car is on the verge of sliding out of the turn when its speed is 28.6 m/s what is the magnitude of the negative lift ${\overrightarrow{F}}_L$, acting downward on the car?
b. The magnitude $F_L$ of the negative lift on a car depends on the square of the car's speed $v^2$, just as the drag force does. Thus the negative lift on the car here is greater when the car travels faster, as it does on a straight section of track. What is the magnitude of the negative lift for a speed of 90 m/s?

Explanation

1. A centripetal force must act on the car because the car is moving around a circular arc, that force must be directed toward the center of curvature of the arc (here, that is horizontally).
2. The only horizontal force acting on the car is a frictional force on the tires is a frictional force.
3. Because the car is not sliding, the frictional force must be a static frictional force `vecf_(s)`.
4. Because the car is on the verge of sliding the magnitude `f_(s)` is equal to the maximum value `f_(s,"max")=mu_(s)F_(N)`, where `F_(N)` is th magnitude of the normal force `vecF_(N)` acting on the car from the track.
Radial calculations: The frictional force `vecf_(s)` is shown in the free body diagram of fig. It is in the negative direction of a radiual axis r that always extends from the center of curvature through thecar as the car moves. The force produces a centripetal acceletation of magnitude `v^(2)//R`. We can relate the force and acceleration by writing Newton.s second law for components along the r axis `(F_("net",r)=ma_(r))` as
`-f_(s)=m(-(v^(2))/R)`
Substituting `f_(s,"max")=mu_(s)F_(N)` for `f_(s)` leads us to
`mu_(s)F_(N)=m((v^(2))/R)`
Vertical calculations: Next let.s consider the vertical forces on the car. The normal force `vecF_(N)` is directed up, in the positive direction of the y axis in fig. The gravitational force `vecF_(g)=mvecg` and the negative life `vecF_(L)` are directed down. The acceleration of the car along the y axis is zero. Thus we can writee Newton.s second law for components along the y axis `(F_("net", y=ma_(y))` as
`F_(N)-mg-F_(L)=0`
or `F_(N)=mg+F_(L)`
Combining results:
Now we can combine our results alogn the two axes by substituting Eq. for `F_(N)` in Eq.. Doing so and then solving for `F_(L)` lead to
`F_(L)=m((v^(2))/(mu_(s)R)-g)`
`=(600kg)(((28.6m//s)^(2))/((0.75)(100m))-9.8m//s^(2))`
`=663.7N~~660N`
b. `F_(L)` is proportional to `v^(2)`.
Calculationis: Thus we can write a ratio of the negative lift `F_(L,90)` at v=90m/s to our result for the negative lift `F_(L)` at v=28.6m/s as
`(F_(L,90))/(F_(L))=((90m//s)^(2))/((28.6m//s)^(2))`
Substituting our known negative lift of `F_(L)=663.7N` and solving for `F_(L,90)` give us
`F_(L,90)=6572N~~6600N`
Upside down racing: The gravitational force is of course, the force to beat if there is a chance of racing upside down,
`F_(g)=mg=(600kg)(9.8m/s^(2))`
`=5880N`
With the car upside down, the negative lift is an upward force of 6600N, which exceeds the downward 5880N. Thus the car could run on a long ceiling provided that it moves at about 90m/s (=324 kmh/h=201mi/h). However, moving that fast while right side up on a horizontal track is dangerous enough, so you are not likely to see upside down racing except in the movies.