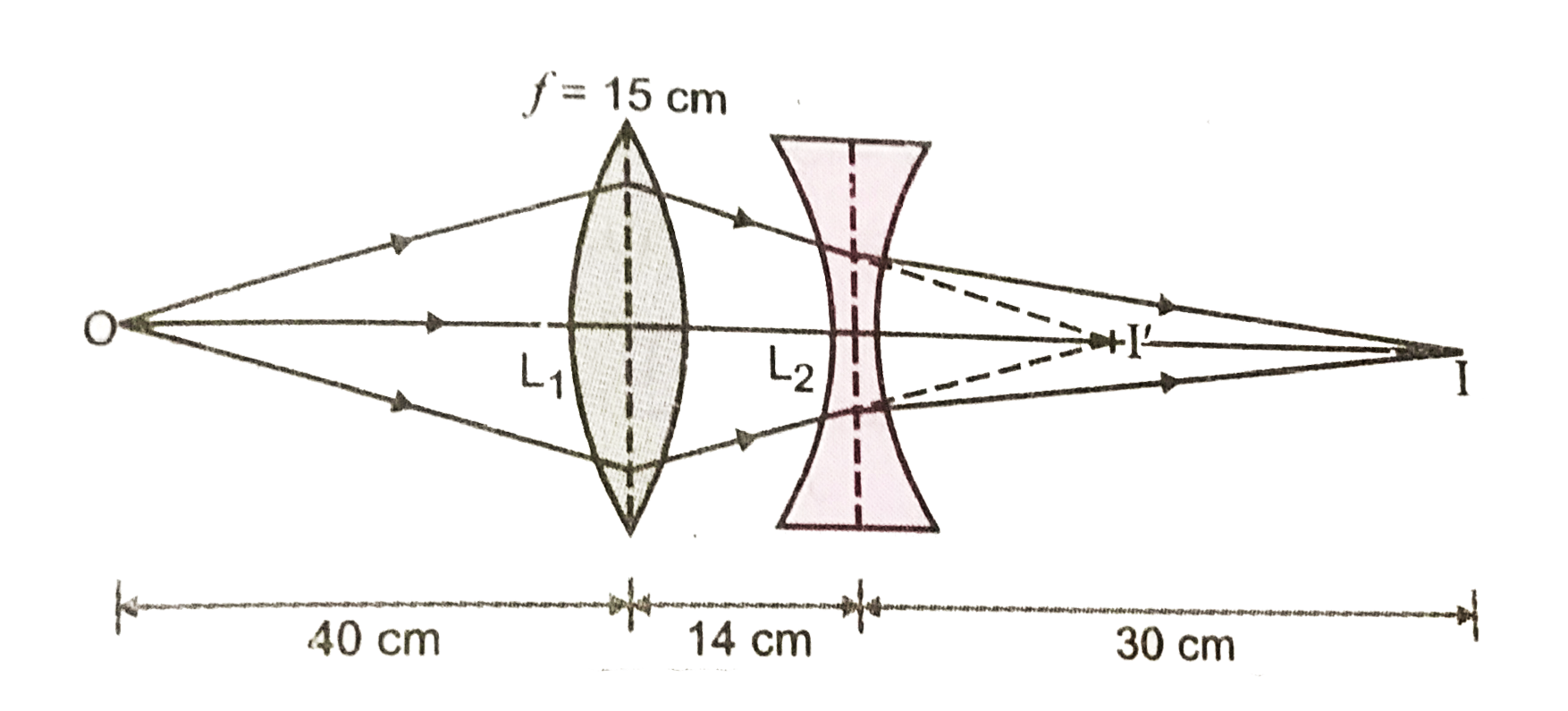
Use the following ray diagram, Fig. 6(b).56 to calculate focal length of lens L2.
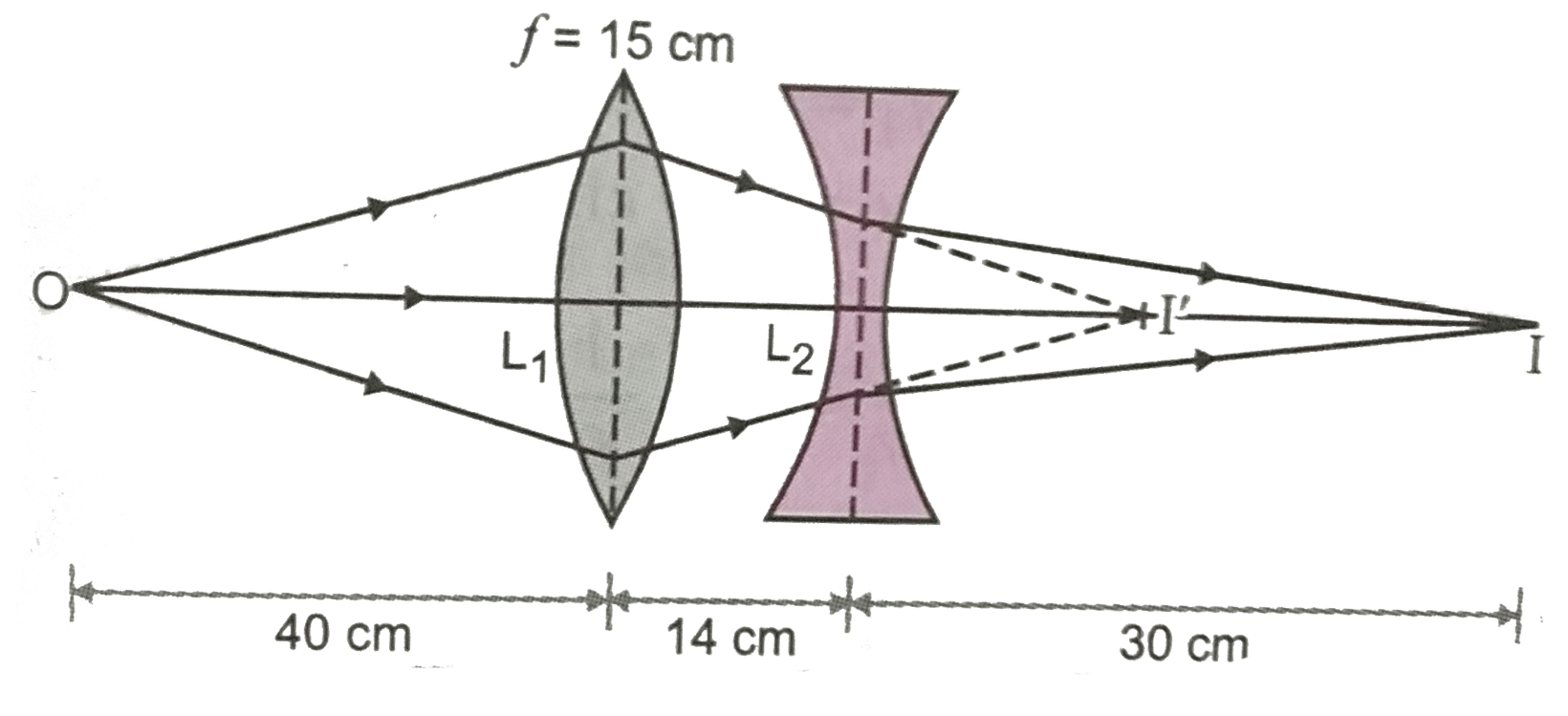
For lens L1,f=15cm,
u=−40cm,
v=?
1v=!f+1u=115−140=5120,v=24cm
The image would have been at I',
where L1I'=24cm.
I' serves as object for L2
u=+(24−14)=10cm,v=30cm,f=?
1f'=1v−1u=130−110=115f=−15cm
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Knowledge Check
Which of the following ray diagrams is correct for the ray of light incident on a lens shown in Fig. ? Choices are given in Fig.
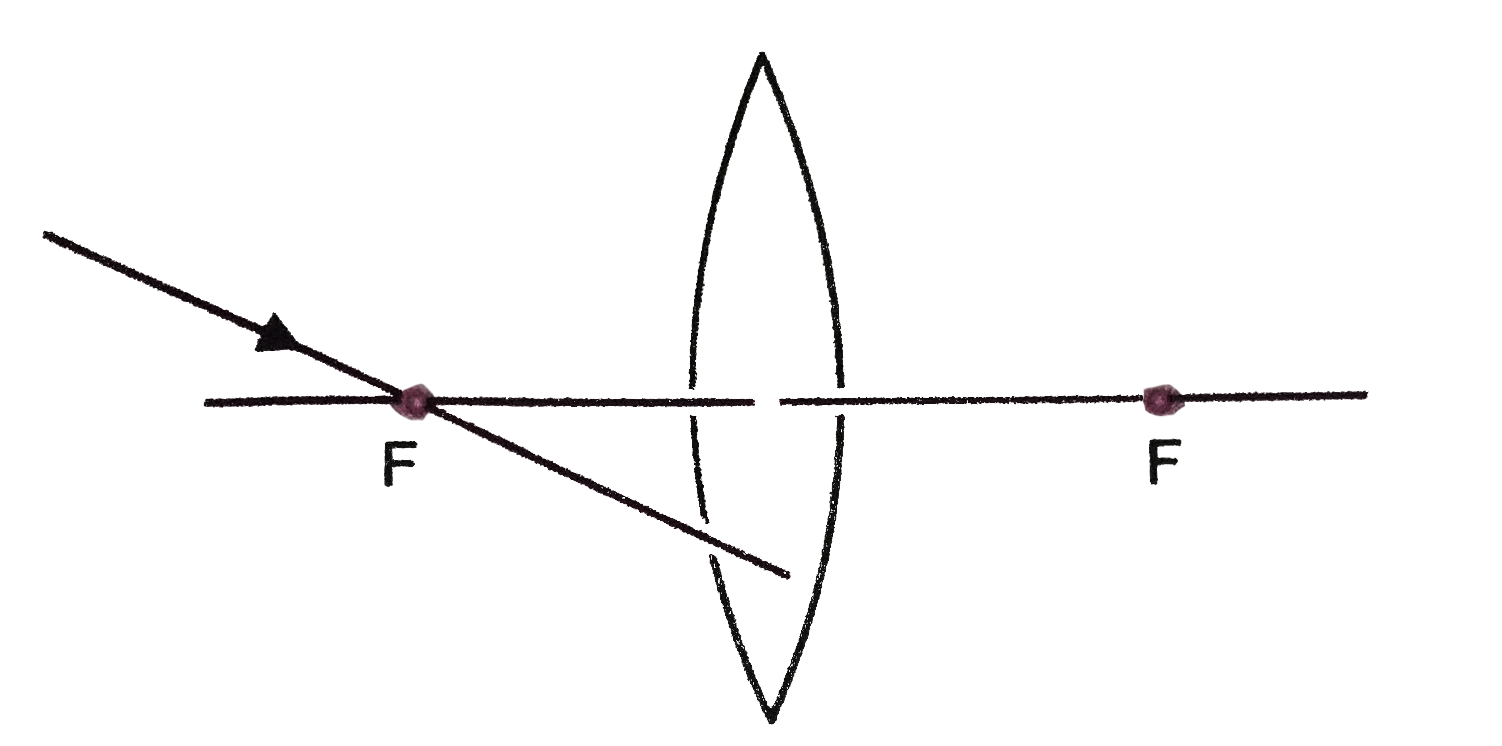 A
A B
B C
C D
D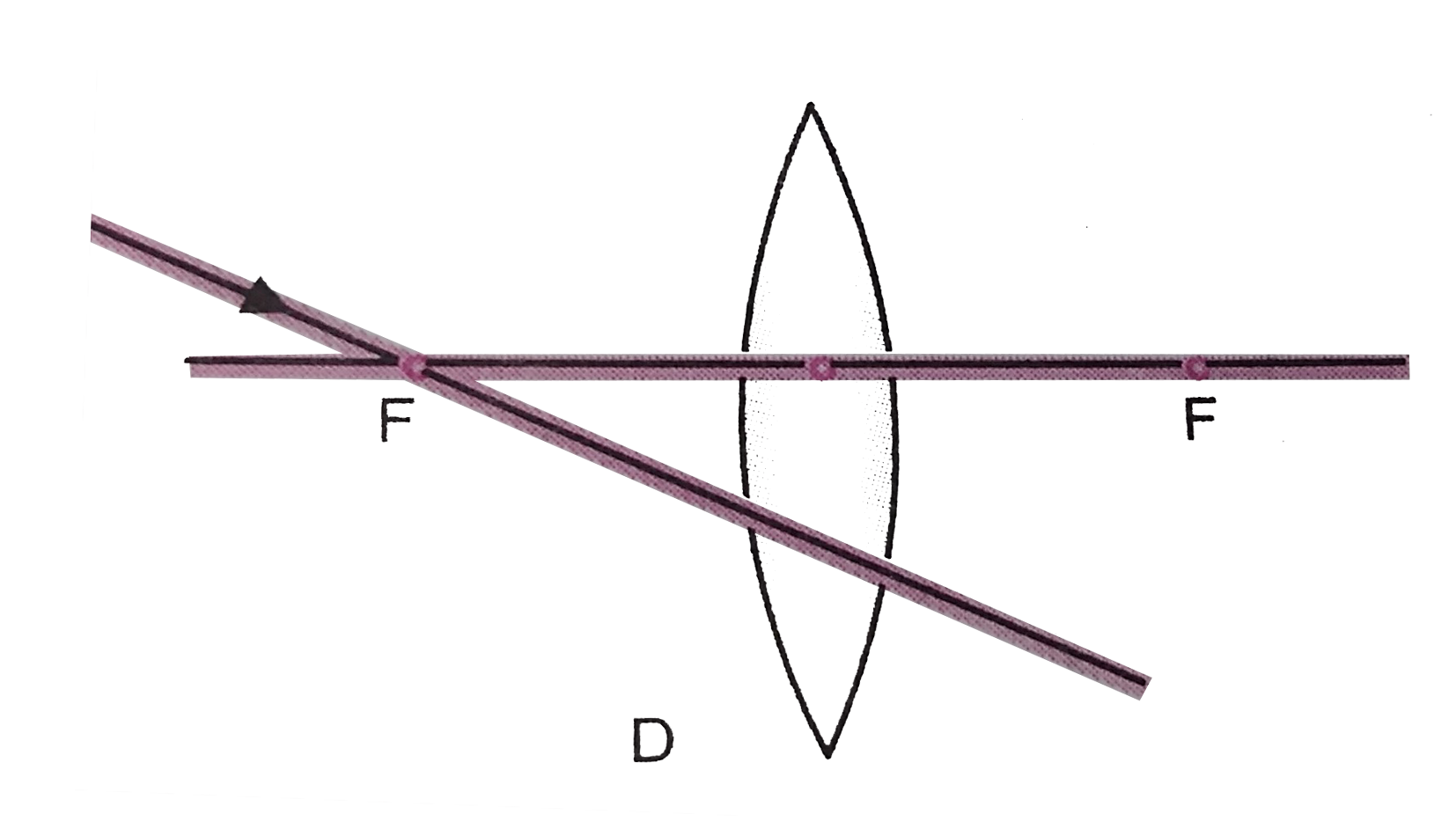
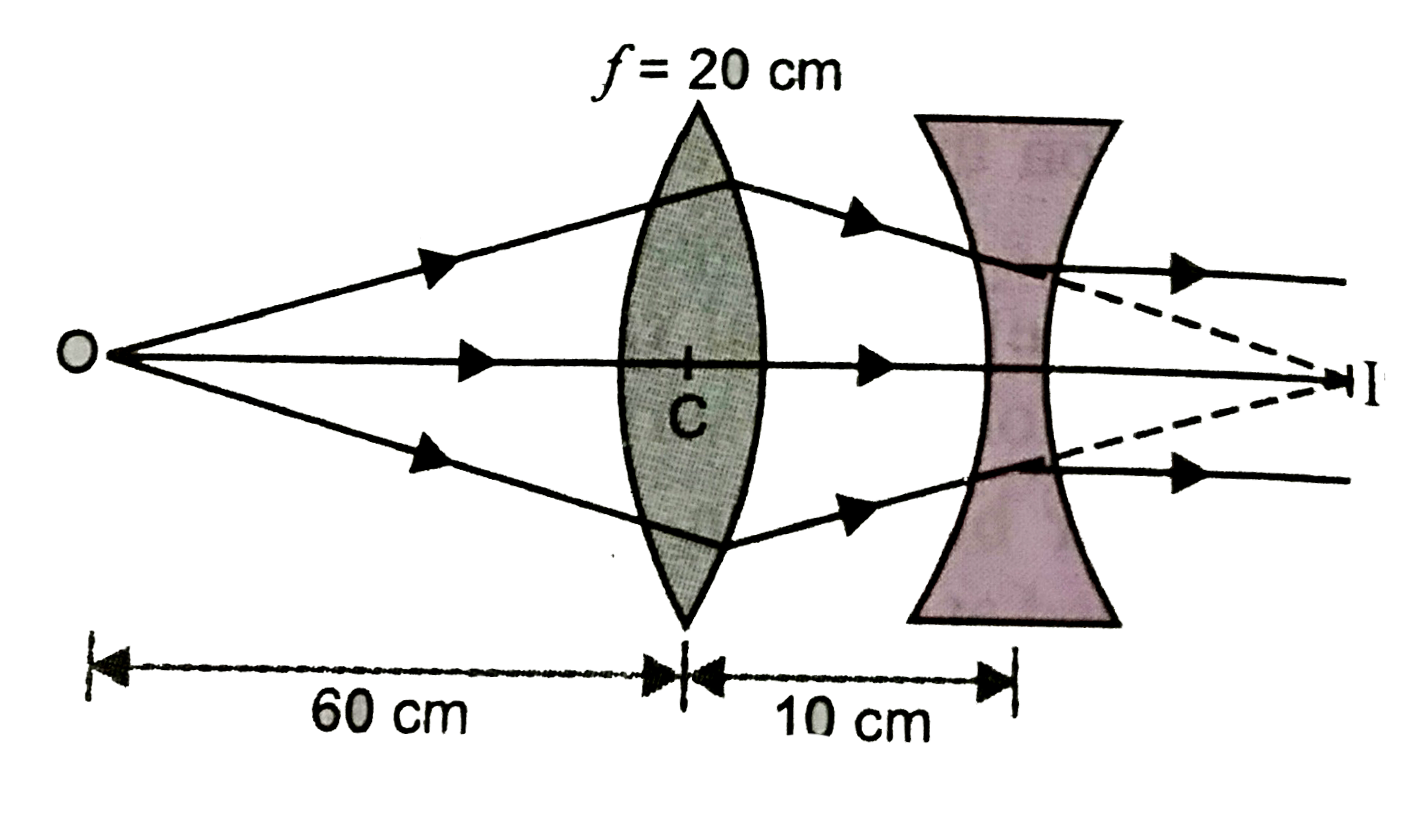
From the ray diagram shown below, calculate the focal length of the other convex lens.

View SolutionFind the focal length of the lens shown in Fig.
View SolutionThe power of a combination of two lenses X and Y is 5 D. If the focal length of lens X be 15 cm:
a) Calculate the focal length of lens Y.
b) State the nature of lens Y.
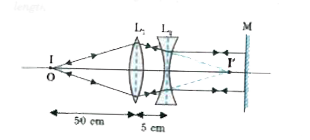
View SolutionIn the following ray diagram the positions of an object O, image I and two lenses L1andL2 and a mirror M are given. The focal length of L1 is 10 cm. Find the focal length of L2.
View SolutionAn object placed 50 cm from a lens produces a virtual image at a distance of 10 cm in front of the lens. Draw a diagram to show the formation of image. Calculate focal length of the lens and magnification produced.
View SolutionDraw ray diagrams showing the image formation by a convex lens when an object is placed
(a) between optical centre and focus of the lens
(b) between focus and twice the focal length of the lens
( c) at twice the focal length of the lens
(d) at infinity , (e) at the focus of the lens
View Solution(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
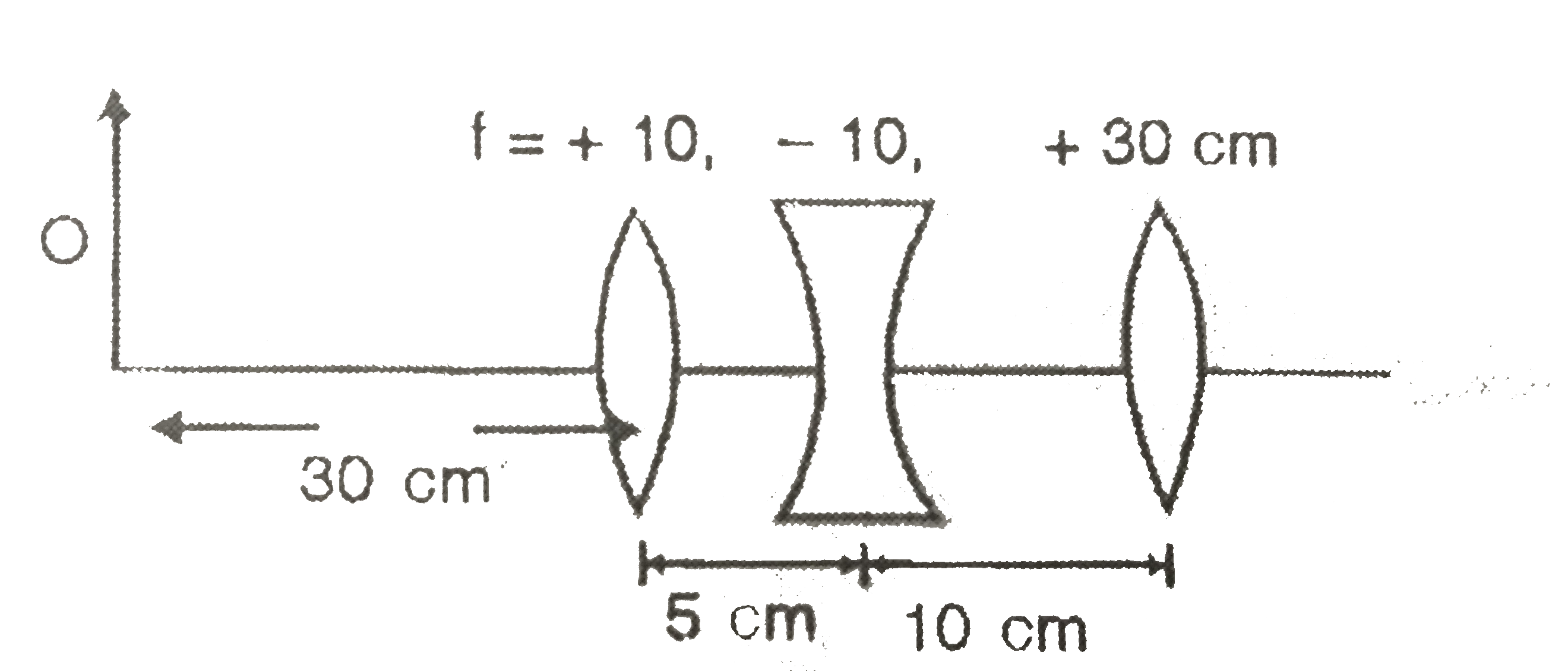
View Solution

 .
. .
.