→A+→B=→C. Vectors →Aand→B if rotated by angle θ in the same sense to from →Aand→B then (θ≠0):
→A+→B=→C
→A+→B≠→C
→A.→B=→A.→B
∣∣→A+→B∣∣=∣∣→C∣∣
The correct Answer is:B, C, D
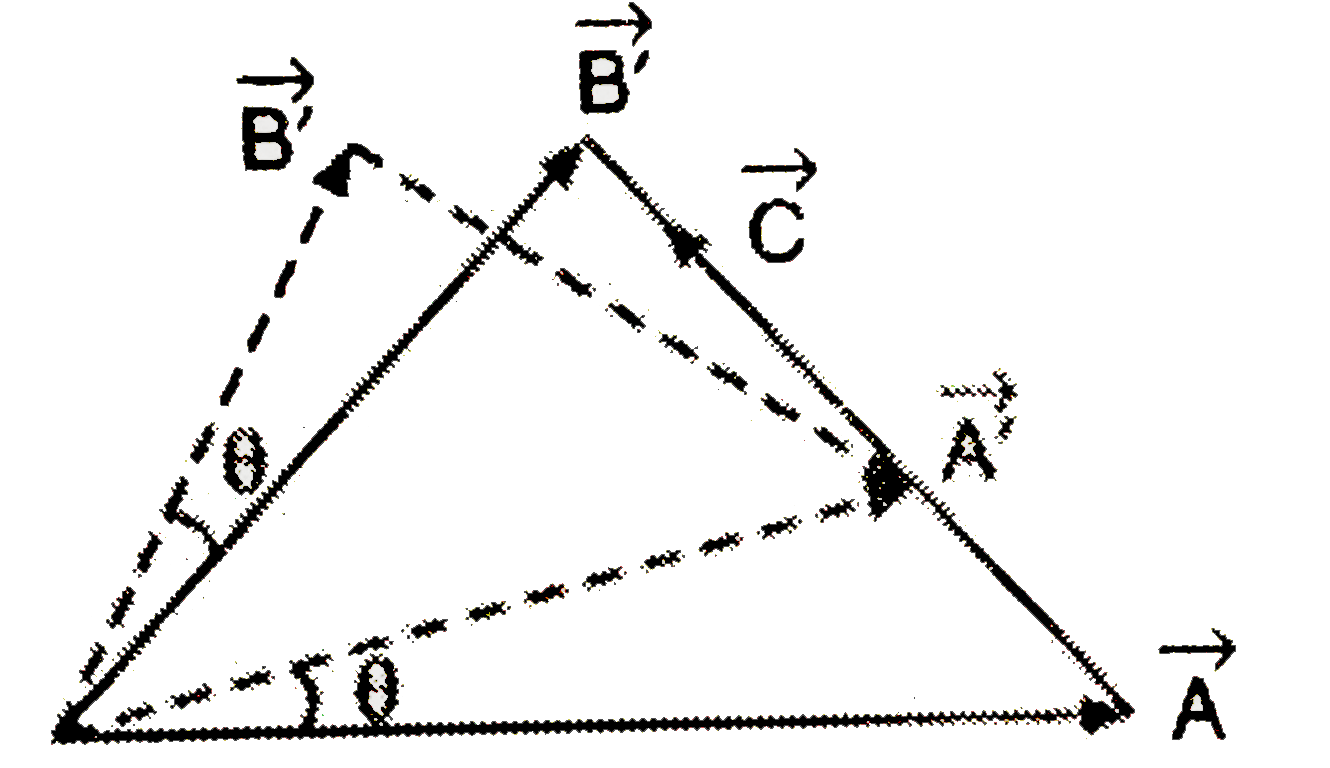
∴ →A+→B≠→A+→B≠→C
→A.→B≠→A.→B
∣∣→A+→B∣∣=∣∣→A+→B∣∣=∣∣→C∣∣
Topper's Solved these Questions
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - ASSERTION- REASON
1 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - MATRIX- MATCH
4 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - OBJECTIVE QUESTIONS
120 Videos
- UNITS AND DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression
6 Videos
Similar Questions
Consider three vectors →a,→band→c. Vectors →aand→b are unit vectors having an angle θ between them For vector veca,|→a|2=→a.→a If →a⊥→band→a⊥→cthen→a∣∣→b×→c If →a∣∣→b,then→a=t→b Now answer the following question: The value of sin(θ2) is (A) 12∣∣→a−→b∣∣ (B) 12∣∣→a+→b∣∣ (C) ∣∣→a−→b∣∣ (D) ∣∣→a+→b∣∣
View SolutionConsider three vectors →a,→band→c. Vectors →aand→b are unit vectors having an angle θ between them For vector veca,|→a|2=→a.→a If →a⊥→band→a⊥→cthen→a∣∣→b×→c If →a∣∣→b,then→a=t→b Now answer the following question: If →c is a unit vector and equal to the sum of →aand→b the magnitude of difference between →aand→b is (A) 1 (B) √2 (C) √3 (D) 1√2
View Solution
Knowledge Check
The vector →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣. The angle between vectors →A and →B is -
A90∘B60∘C75∘D45∘→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
Aπ/2Bπ/4C3π/4DπThe two vectors →A and →B are drawn from a common point and →C=→A+→B. Then, the angle between →A and →B is
A90∘ if C2>A2+B2Bgreater than 90∘ if C2<A2+B2Cgreater than 90∘ if C2>A2+B2Dless than 90∘ if C2>A2+B2
Consider three vectors →a,→band→c. Vectors →aand→b are unit vectors having an angle θ between them For vector →a,|→a|2=→a.→a If →a⊥→band→a⊥→cthen→a∣∣→b×→c If →a∣∣→b,then→a=t→b Now answer the following question: If veccisasunit→−−→rsuchtˆveca.vecb=veca.vecc=0 and theta= (pi/6) then veca=(A)+-1/2(vecbxxvecc)(B)+-(vecbxxvecc)(C)+-2(vecbxxvecc) (D) none of these
View SolutionIf three unit vectors →a,→band→c satisfy→a+→b+→c=→0. Then find the angle between →aand→b.
View SolutionIf →a,→b,→c are unit vectors such that →a.Vecb=0=→a.→c and the angle between →band→cisπ3 , then find the value of ∣∣→a×→b−→a×→c∣∣
View Solutionif →a,→b,→c are three vectors such that →a+→b+→c=→0 then
View SolutionIf (→a×→b)×→c=→a×(→b×→c), where →a,→b and →c are any three vectors such that →a.→b≠0,→b.→c≠0, then →a and →c are:
View Solution
