v=gt,h=12gt2,v=u+at,v2=2gh
v=u+at is the fundamnetal kinematical equation of motion while other are kinematical equations for a freely falling body
Topper's Solved these Questions
- GRAVITATIONBOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPLETE THE ANALOGY
4 Videos
- GRAVITATIONBOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - MATCH THE FOLLOWING
2 Videos
- GRAVITATIONBOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - TRUE OR FALSE IF FALSE, WRITE THE CORRECT SENTENCE
12 Videos
- ENVIRONMENTAL MANAGEMENT BOOK - TARGET PUBLICATIONCHAPTER - ENVIRONMENTAL MANAGEMENT EXERCISE - APPLY OUR KNOWLEDGE
28 Videos
- HEATBOOK - TARGET PUBLICATIONCHAPTER - HEATEXERCISE - Values to remember
10 Videos
Similar Questions
Velocity at a general point P(x, y) for a horizontal projectile motion is given by
v=√(v2x+vy2),tanα=vyvx
αis angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by x=vxt=ut
y=-(1/2)gt2
eliminating t, we get y=−(1/2)gx2u2
An aeroplane is flying horizontally with a velocity of 720 km/h at an altitude of 490 m. When it is just vertically above the target a bomb is dropped from it. How far horizontally it missed the target?
View SolutionLet y = uv be the product of the functions uandv. Find y'(2) if u(2)=3,u'(2)=–4,v(2)=1,andv'(2)=2.
View Solution
Knowledge Check
Which one of the following is the equation for Position - Time relation?
A) S=ut+1/2at2
B) V = u + at
C) U = y + at
D) 2as=v2–u2AS=ut+1/2at2BV = u + atCU = y + atD2as=v2–u2Statements : X>Y,Y>Z,Z=V,C<W
Conclusions : I. Y=V
II. Y>VAIf only conclusion I followsBIf only conclusion II followsCIf neither conclusion I nor II followsDIf both conclusion I and II follow.If y=√u ,u=(3-2v)v and v=x2, then dydx=
A4−3x2√3−2x2B3+4x2√3−2x2C3−4x2√3−2x2D4+3x2√3−2x2
uandv are two non-collinear unit vectors such that ∣∣∣ˆu+ˆv2+ˆu׈v∣∣∣=1. Prove that |ˆu׈v|=∣∣∣ˆu−ˆv2∣∣∣.
View SolutionLet u,v,w be real numbers in geometric progression such that u>v>w. Suppose u40=vn=w60. Find the value of n .
View SolutionA jet plane files horizonally at a height h at a speed v. An anti-aircraft gun fires a shell at the plane when it is
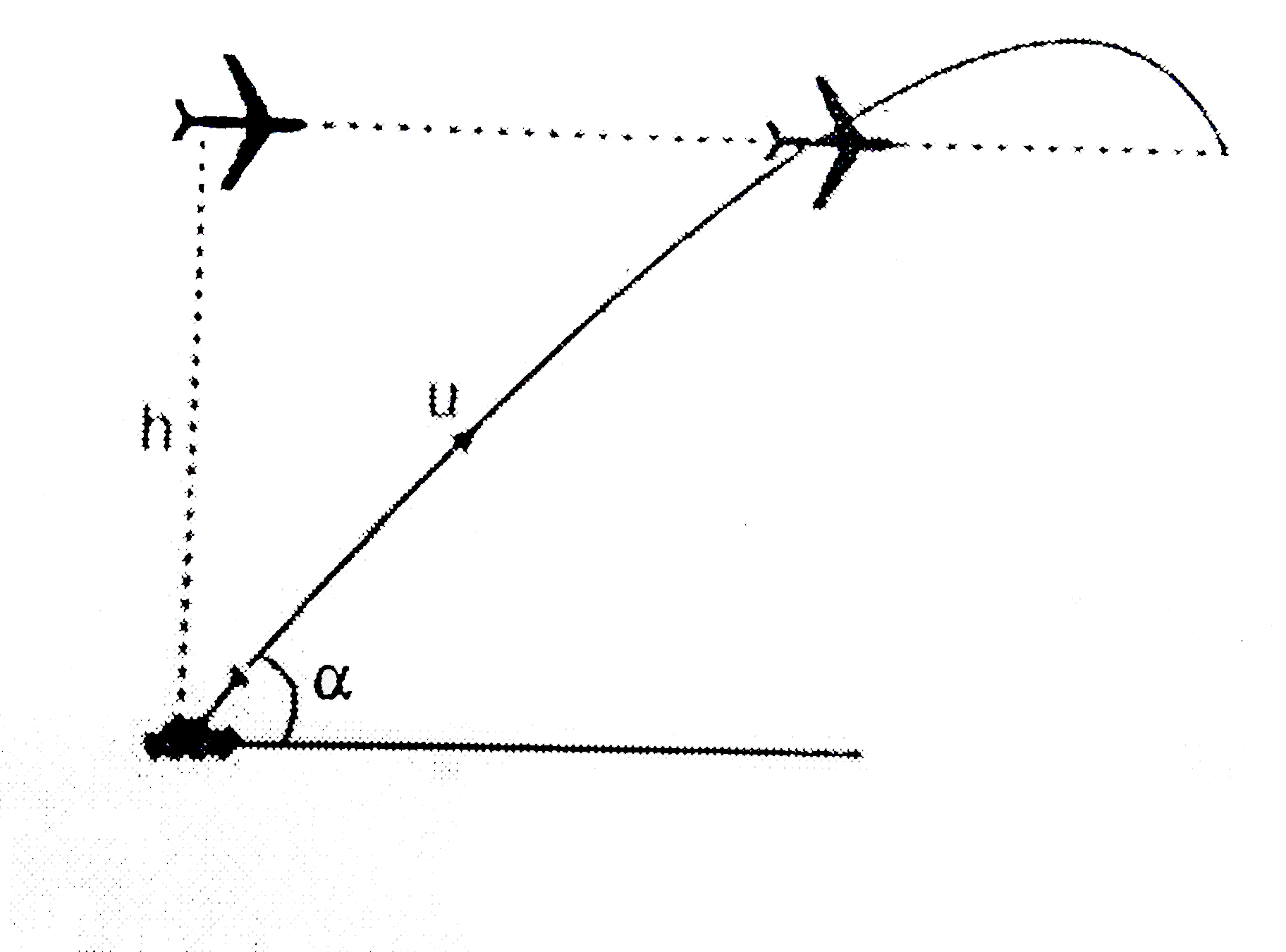
vertically above the gun. Show that the minimum muzzle speed required to hit the plane is √v2+2gh at an angle tan−1√2ghv
View SolutionAn Aeroplane flies horizontaily at a height h at a speed v. An anti-air craft gun fires a shell at the plane when it is vertically above the gun. Show that the minimum muzzle velocity required to hit the plane is √v2+2gh at an angle tan−1(√2ghv)
View SolutionFor any two vectors →uand→v prove that (→u.→v)2+|→u×→v|2=|→u|2|→v|2
View Solution
