v,T,ρ and λ denote ,surface tension, mass density and wavelength, respectively In an experiment v depends on T,p and λ respectively .The value of v is proportional to
sqrt((T)/(lambda))
√Tpλ
√λpT
sqrt((T)/( p lambda))
The correct Answer is:b
v=KTapρbλc
LHS=[M0LT−1]
RHS=[M0LT−1]
=[MT−2]a[ML−3]b[L]c
=[Ma+bL−3b+cT−2a]
According to homogeneity principal
LHS - RHS
[M0LT−1]=[Ma+bL−3b+cT−2a]
∴a+b=0
∴a=−b...(i)
−3b+c=1...(ii)
−2a=−1...(iii)
∴c=−12
b=−a=−12
−3b+c=1
⇒−3(−12)
∵v=KTaρbλc=KT12ρ−12λ−12=K√Tρλ.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Assertion Reasoning16videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - NEET Questions23videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Erros Of Measurement31videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test29videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
Frequency is the function of density ρ, length λ and tension T. The period of oscillation is proporttional to
Aρ1/2λ2T1/2Bρ3/2λ3/2T−1/2Cρ1/2λ3/2T−3/3Dρ1/2λ1/2T3/2 - Question 2 - Select One
The speed (v) of ripples on the surface of waterdepends on surface tension (σ), density (ϕ) and wavelength (λ). The square of speed (v) is proportional to
AσρλBρσλCλσρDρλσ - Question 3 - Select One
If v,p and E denote velocity, lenear momentum and KE of the paritcle respectively, then
Ap=dEdvBp=dEdtCp=dvdtDp=dEdv×dEdt
If 'C' and 'V' represent capacity and voltage respectively then what are the dimensions of λ, where CV=λ ?
View SolutionIf λv,λx and λm represents the wavelength of visible light X-ray and microwave respectively then :
View SolutionThe plots of intensity v/s wavelength for three at temperatures T1,T2 & T3 respectively. Their temperatures are such that (Decreasing order)
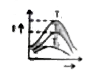 View Solution
View SolutionIn the figure shown a sinusoidal wave is generated at the end 'A'. The wave travels along positive x−axis and during its motions it encounter another string BC at the junction 'B' at x=0. The density of strings AB and BC and ρ and 9ρ respectively and their radii of cross sections are 2r and r. The wave funcation. amplitude and wavelength of incident wavs are respectively yr,Ar,λr and yt,At,λt repectively

The ratio of wavelengths λr to λt (i.e. λr:λt) will beView SolutionIn the figure shown a sinusoidal wave is generated at the end 'A'. The wave travels along positive x−axis and during its motions it encounter another string BC at the junction 'B' at x=0. The density of strings AB and BC and ρ and 9ρ respectively and their radii of cross sections are 2r and r. The wave funcation. amplitude and wavelength of incident wavs are respectively yr,Ar,λr and yt,At,λt repectively

The ratio of wavelengths λr to λt (i.e. λr:λt) will beView Solution

