Water and liquid are filled up behind a square wall of side. Find out
a. pressures at A,B and C
b. forces in part AB and BC
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
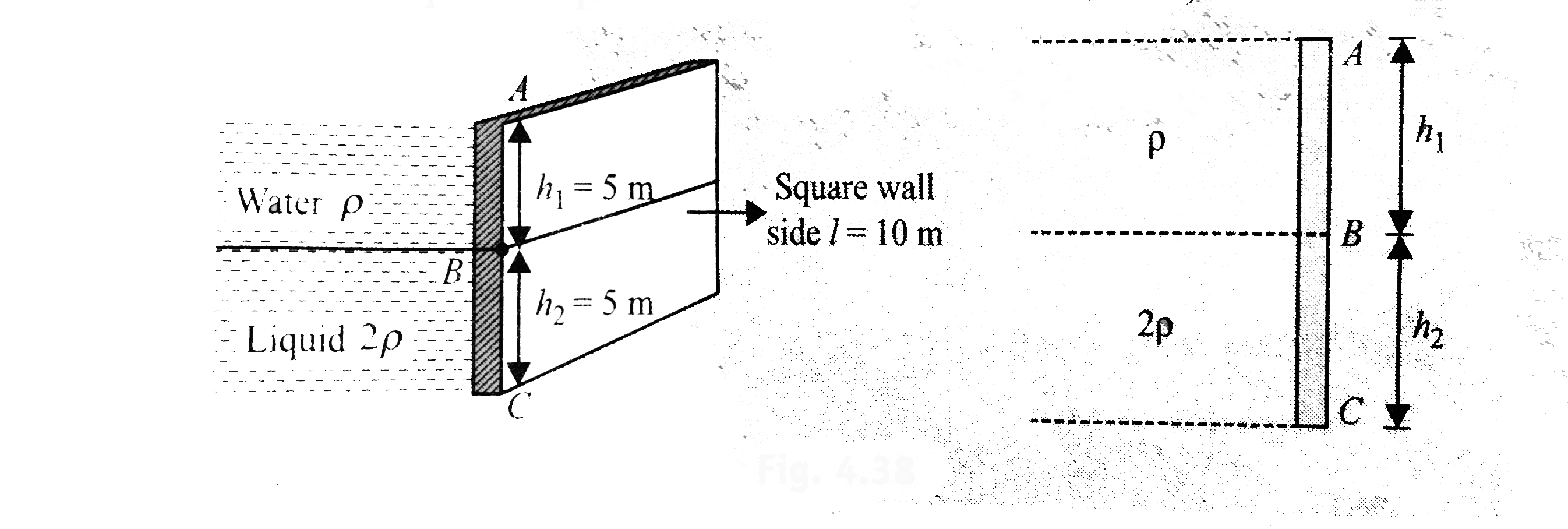
As there is no liquid above A
pressure at A is pA=0
Pressure at B is pB=ρgh1
pressure at C is pC=ρgh1+2ρgh2
b. Force at A is zero. Take a strip a of width dx at a depth 'x' in part AB. Pressure is equal to ρgx.
Force on strip = pressure × area

dF=ρgldx
Total force up to B,
FB=∫h0ρgldx=ρglh212
=1000×10×10×5×52=1.25×106N
In part BC for force take a elementary strip of width dx in portion BC. Pressure is givenby
ρgh1+2ρg(x−h1)
Force on the elementary strip = pressure × area
∴dF=[ρgh1+2ρg(x−h1)]ldx
The limit of x will be x=h1 to x=h1+h2=l

The force on part BC is F=∫h1+h2h1[ρgh1=2ρg(x−h−10]l
But h1+h−2=l=[ρgh1x+2ρg[x22−h1x]]lh1
=ρgh1h2l+ρgl(l−h1)2
=ρgh2l[h1+h2]=ρgh2l2
=1000×10×5×10×10
=5×106N
c. Method 1
Total =5×106+1.25×106=6.25×106N
Taking torque about A the total torque of force in AB is
∫dx=∫F0ρgxldxx
[ρglx33]h10=ρglh313=1000×10×10×1253
=1.25×1073Nm
The total torque of force in BC about A is given by
∫dFx=∫lR[ρgh1+2ρg(x−h1)]ldx.x
ρgh1h2l[h1+h22]+ρgh22l[h1+2h23]
=2.5×7.5×106+62.53×106
118.753×106Nm
Total torque =11.875×1073+1.25×1073
=13.125×1073Nm
Total torque = Total force × Distance of point of application of force from top =Fxp
⇒6.25×106xp=13.125×1073Nm
⇒xp=7m
Method 2. Pressure diagram on the wall
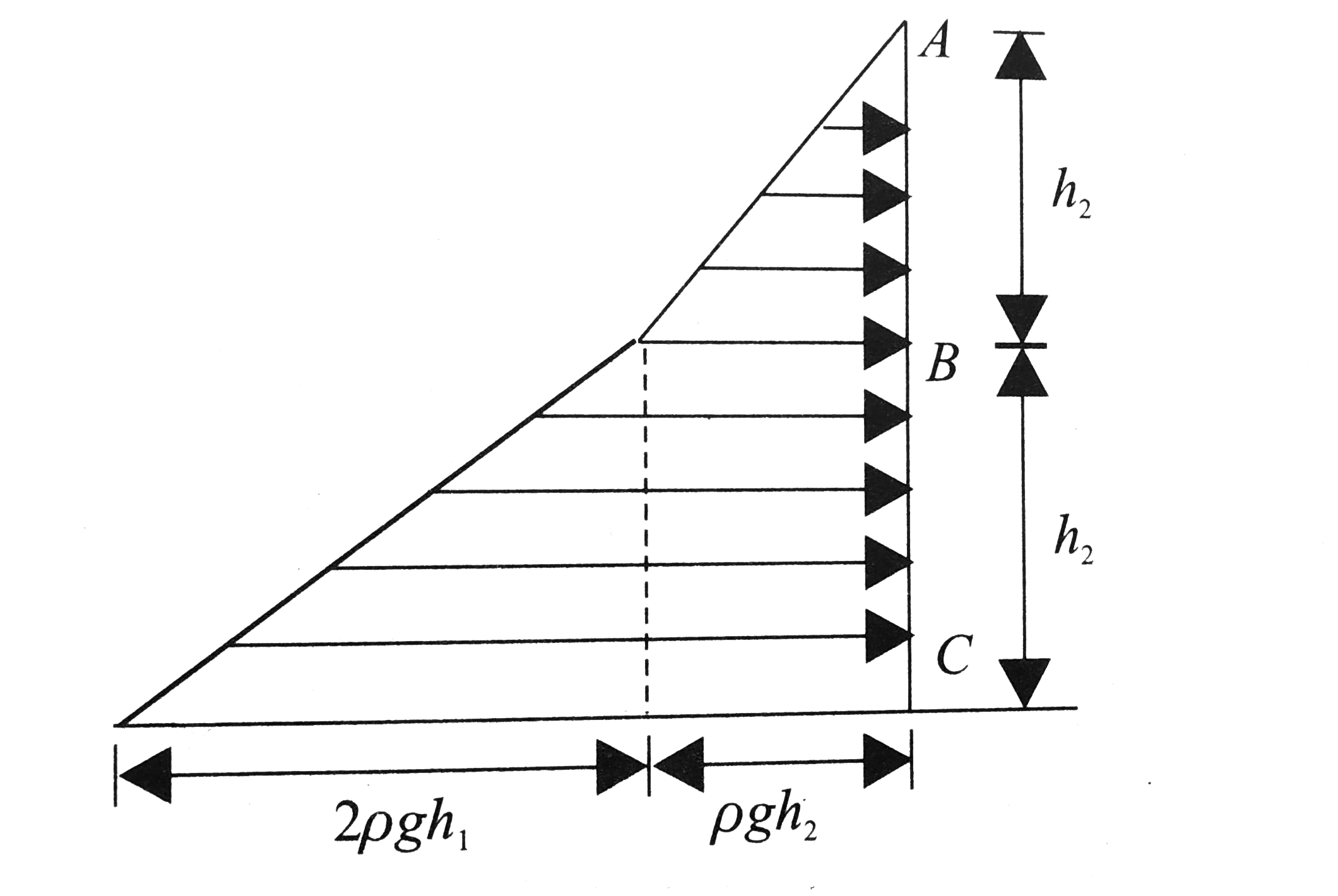
Total force on the wall per unit width of the wall = Area of presure diagram.
Fb=12(ρgh1)h1+ρgh1h2+12(2ρgh2)h2
=ρg[h212+h22]+ρgh1h2
F∂=F=12ρg21+ρglh2[h1+h2]
6.25×106N
Total force on AB part FAB=12ρglh1=1.25×106N
Total force on BC part FBC=ρglh2(h1+h2)=5×106N The total force will act at the centroid of the pressure diagram. Let the distance of centroid of pressure diagram be 'r' from A
r=ρgh212×23h1+2ρgh222(h1+23h2)+(ρgh1h2)(h1+h22))(ρgh2012+ρh22+ρgh1h2)
=h313+h22(h1+23h2)+h1h2(h1+h22)h212+h22+h21
r=[13+(1+23)+(1+12)]512+1+1=7252×5=7m
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
_S01_024_Q01.png)
Water and liquid is filled up behind a square wall of side l
Find out (a). Pressure at A, B and C
(b). Forces in part AB and BC
(c). Total force and point of application of force. (Neglect atmosphere pressure in every calculation.)
View SolutionHydrostatics: Pressure due to a Liquid Column | Equating pressure in U-tube Problems | Force and Torque on container wall (point of application of force)
View Solution
Knowledge Check
Mercury is completely filled in a rectangular take of height 72 cm. The atmospheric pressure at the place is 72 cm. of Hg. Find the distance in cm of point of application from bottom of tank of the net force , on the inner surface of the side vertical wall of tank.
A32 cmB16 cmC74 cmD42 cmA capillary tube is dipped in a liquid. Let pressure at point A,B and C be pApB and pC respectively, then
 ApA=pB=pCBpA=pB<pCCpA=pC<pBDpA=pC>pB
ApA=pB=pCBpA=pB<pCCpA=pC<pBDpA=pC>pB
_S01_031_Q01.png)
In a given arrangement (a) find out velocity of water coming out of C
(b). Find out pressure A, B and C
View SolutionThree force are applied to a square plate as shown in the figure. Find the magnitude, direction and point of application of the resultant force if this point is taken on the side BC.
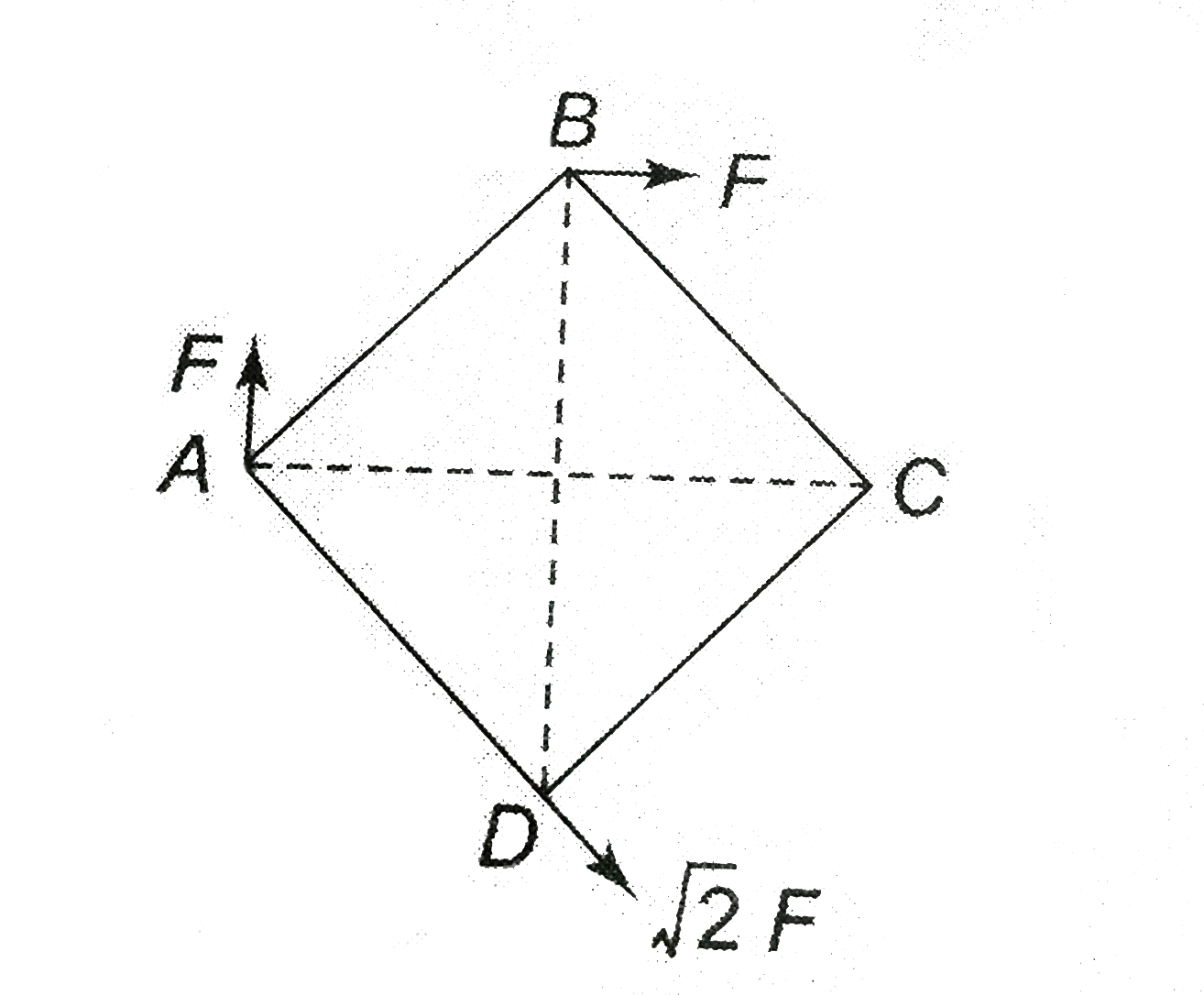
View SolutionThree forces are applied to a square plate as shown in Figure. Find the modulus, direction, and the point of application of the resultant force, if this point is taken on the side BC.

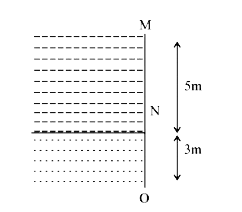
View SolutionTwo liquids of densities p1andp2(p2=6p1) are filled up behind a square wall of side 8 m as shown in figure. The liquids have height as shown. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)
View SolutionTwo parallel unlike forces of magnitudes 15 N and 10 N are acting at point A and B respectively. If C is the point of action of resultant, then AB/BC is
View SolutionTwo parallel unlike forces of magnitudes 15 N and 10 N are acting at point A and B respectively. If C is the point of action of resultant, then AB/BC is
View Solution
