Water at 10∘C is present in a thermally insulated container. Calculate the ratio of mass of ice formed and initial mass of water, if a small crystal of ice is thrown into it.
115
117
215
18
d) let initial mass of water in the container be m.
m1 = the mass of water converted into ice.
At final thermal equilibrium state, temperature of mixture should be zero.
∴ Heat loss by water = heat of fusion of water.
or ms[0−(−10)]= m1L
or m×1×10=m1×80) or m1m=1080=18
Topper's Solved these Questions
- HEAT, TEMPERATURE AND CALORIMETRYBOOK - BITSAT GUIDECHAPTER - HEAT, TEMPERATURE AND CALORIMETRYEXERCISE - Bitsat archives
9 Videos
- GRAVITATIONBOOK - BITSAT GUIDECHAPTER - GRAVITATIONEXERCISE - BITSAT Archives
15 Videos
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 40
1 Videos
Similar Questions
On a winter day when the atmospheric temperature drops to −10∘C , ice forms on the surface of a lajke. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts forming. Density of water =1000kgm−3 , latent heat of fusion of ice =3.36×105Jkg−1 and thermal conductivity of ice =1.7Wm−1^(@)C^(-1) . Neglect the expension of water on freezing.
View SolutionOn a winter day when the atmospheric temperature drops to −10∘C, ice form on the surface of a lake.
(a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed.
(b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts froming. Density of water =1000kg/m3, latent heat of fusion of ice =3.36×105J/kg and thermal conductivity of ice =1.7W/m−∘C. Neglect the expansion of water on freezing
View Solution
Knowledge Check
Some pure ice is put in brine taken in a perfect insulated container at 0∘C. The mass of ice
Awill not change with timeBwill increase with timeCwill increase with timeDwill first increase than decrease with timeA vessel contains 10–1kg of ice at 0∘C. Now steam is passed into the vessel to melt ice. Neglecting the thermal capacity of the vessel, find the mass of water in the vessel when all ice melts into water.
A12.5 gmB100 gmC112.5 gmD125 gm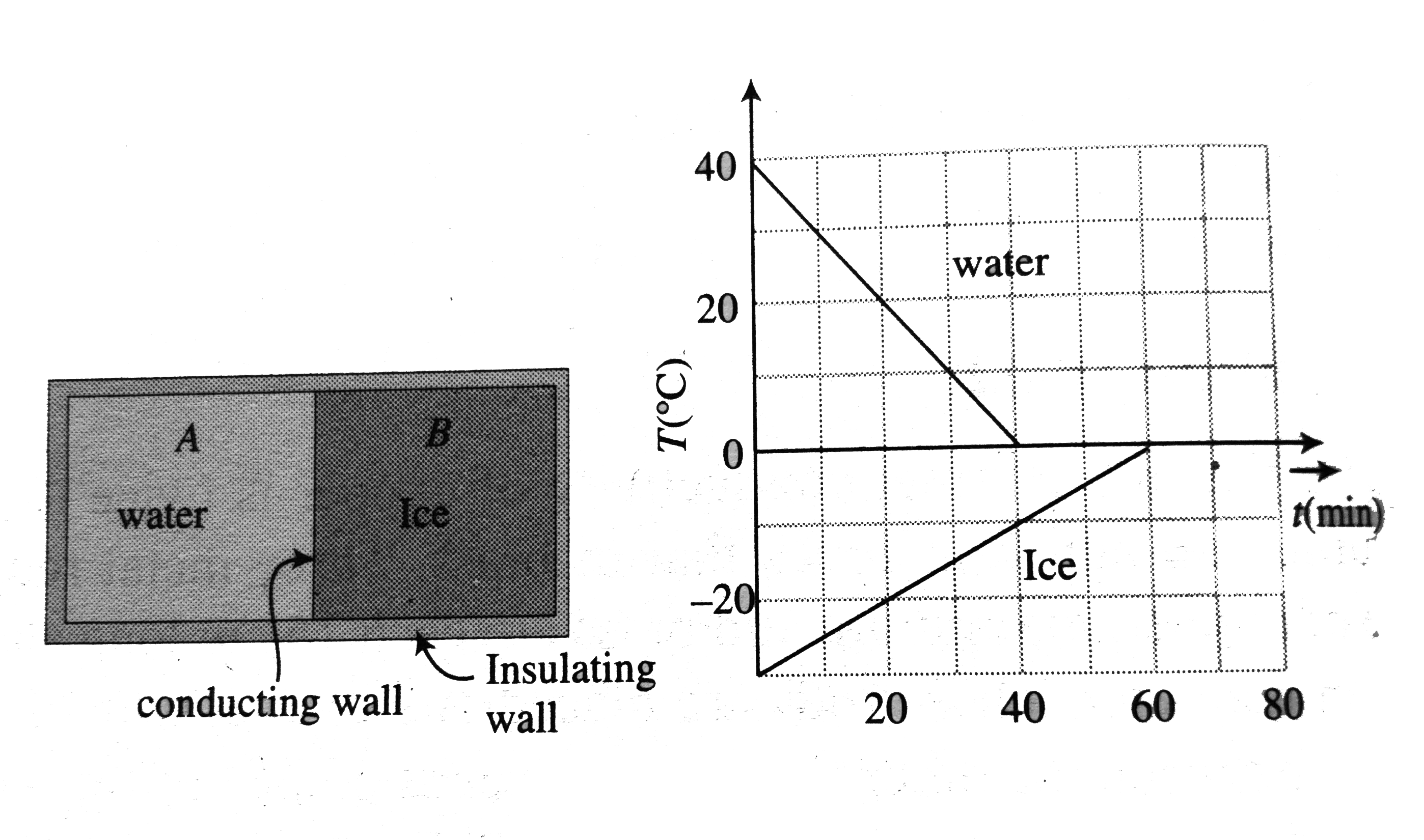
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal toA0.36 kgB1.2 kgC2.4 kgD3.6 kg
(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at 25∘C, and the ice comes directly from a freezer at −15∘C, what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
View SolutionFor same mass of water and ice, why ice floats over water?
View Solution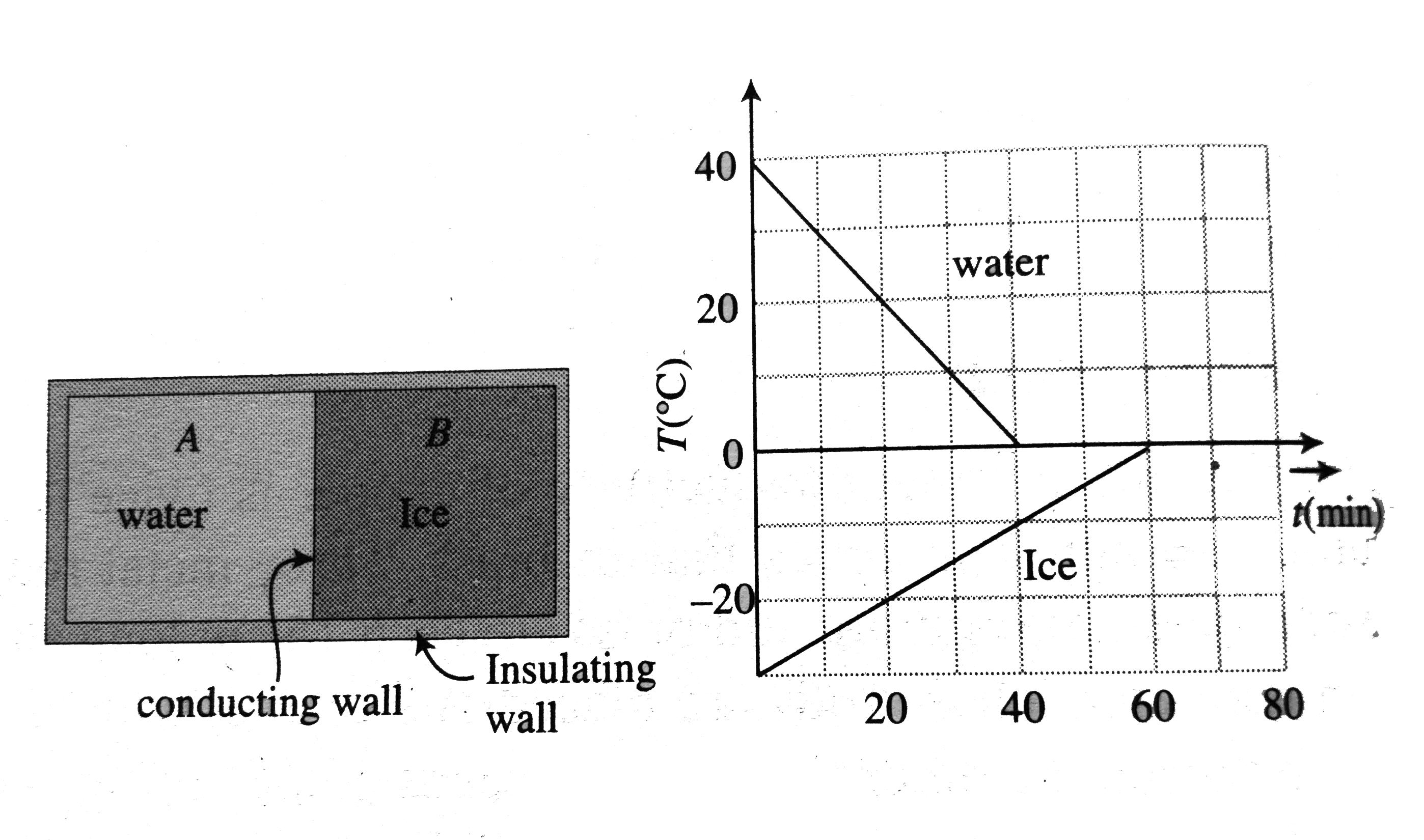
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution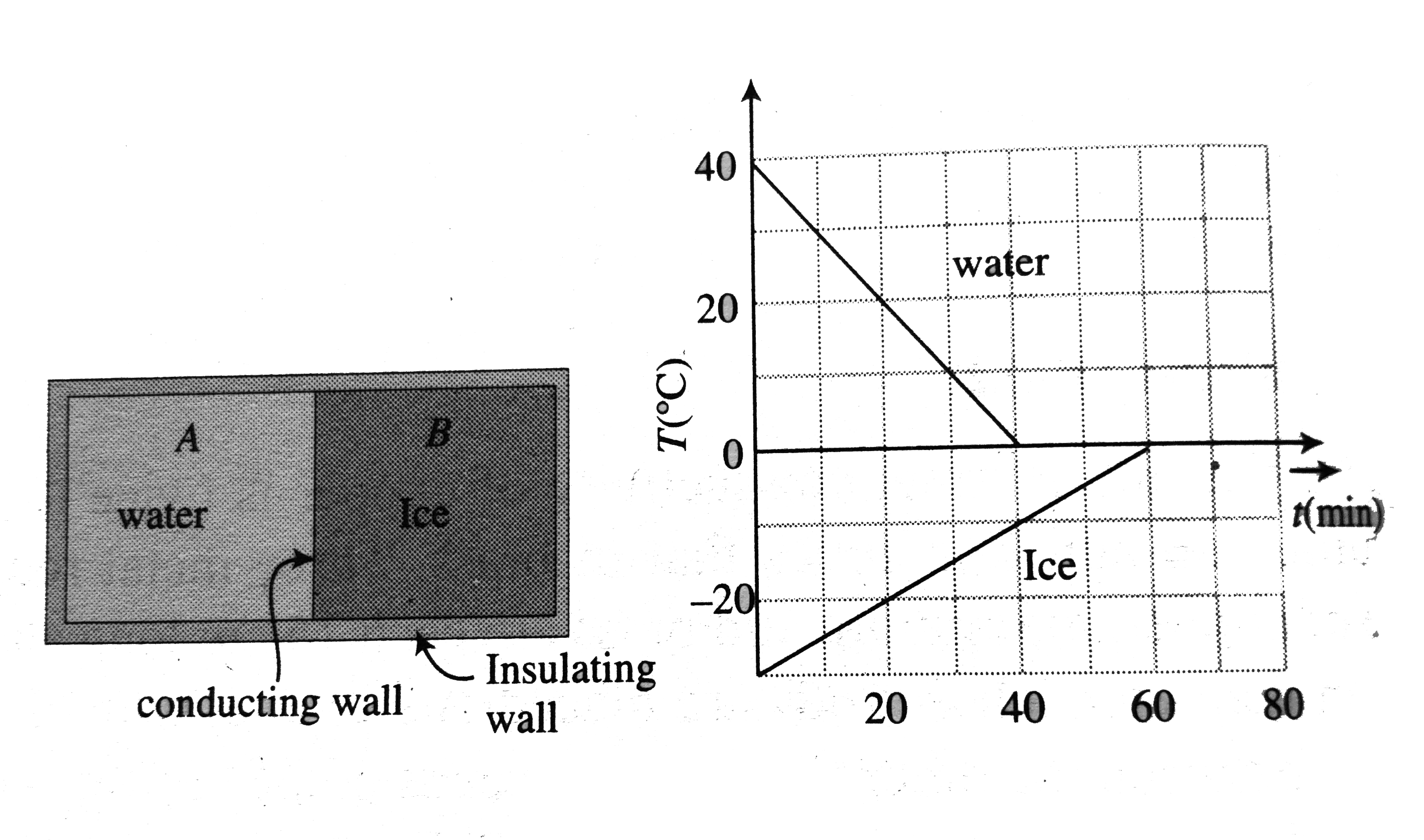
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
View Solution80g of water at 30∘C is poured on a large block of ice at 0∘C. The mass of ice that melts is
View Solution
