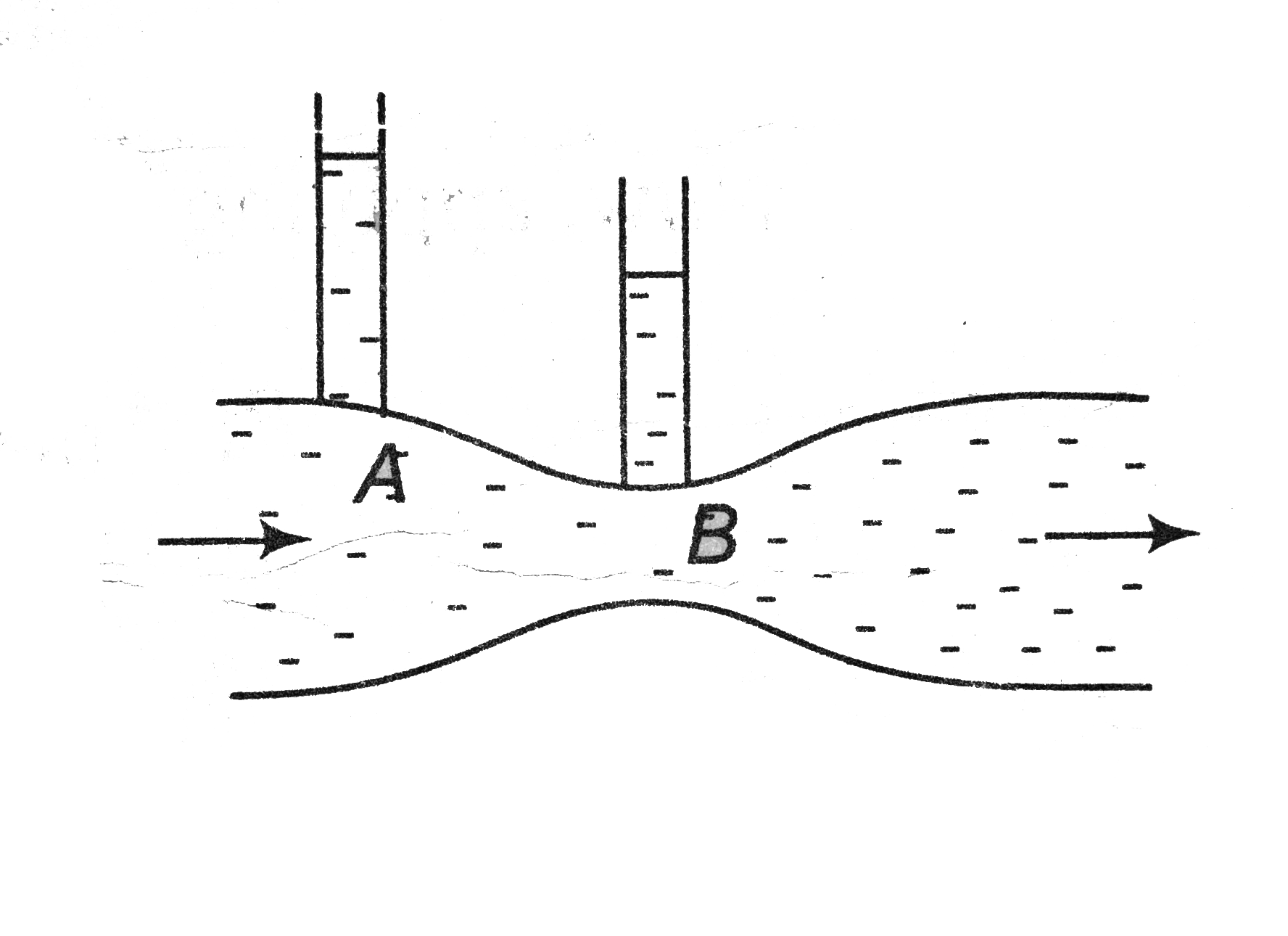
Water flows through a horizontal tube as shown in figure. If the difference of heights of water column in the vertical tubes is 2 cm and the area of cross section at A and B are 4cm2and2cm2 respectively, find the rate of flow of water across any section.

130×10−6m3/s
146×10−6m3/s
160×10−6m3/s
170×10−6m3/s
The correct Answer is:B
vAaA=vB×aB=vA×4=vB×2vB=2vA………i
Again 12,ρv2A+ρghA+pA=12ρv2B+ρghB+pB
⇒12ρg2A+pA=12ρv2B+pB (as hA=hB)
⇒pA−pB=12ρ(v2B−v2A)=12×1×(4v2A−v2A)
⇒2x1×1000=12×1×3v2A
pA=pB=2cm of water column =2×1×1000dyn/cm2
∴vA=√40003=36.51cm/s
So, rate of flow =VaaA=36.51×4=146cm3/s.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Water flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 respectively. Find the rate of flow of water across any section.
 .
.
View SolutionWater flows in a horizontal tube as shown in figure. The pressure of water changes by 600N/m2 between x and y where the areas of cross-section are 3cm2 and 1.5cm2 respectively. Find the rate of flow of water through the tube.

View Solution
Knowledge Check
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=ghWater flows through a non-uniform tube of area of cross section A, B and C whose values are 25, 15 and 35cm2 resprectively. The ratio of the velocities of water at the sections A,B and C is
A5:3:7B7:3:5C21:35:15D1:1:1
Water flows ina horizontla tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B whre the areas of cross section asre 30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
 ,
,
View SolutionWater flows in a horizontal tube (see figure). The pressure of water changes by 700 Nm−2 between A and B where the area of cross section are 40cm2 and 20cm2, respectively. Find the rate of flow of water through the tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.
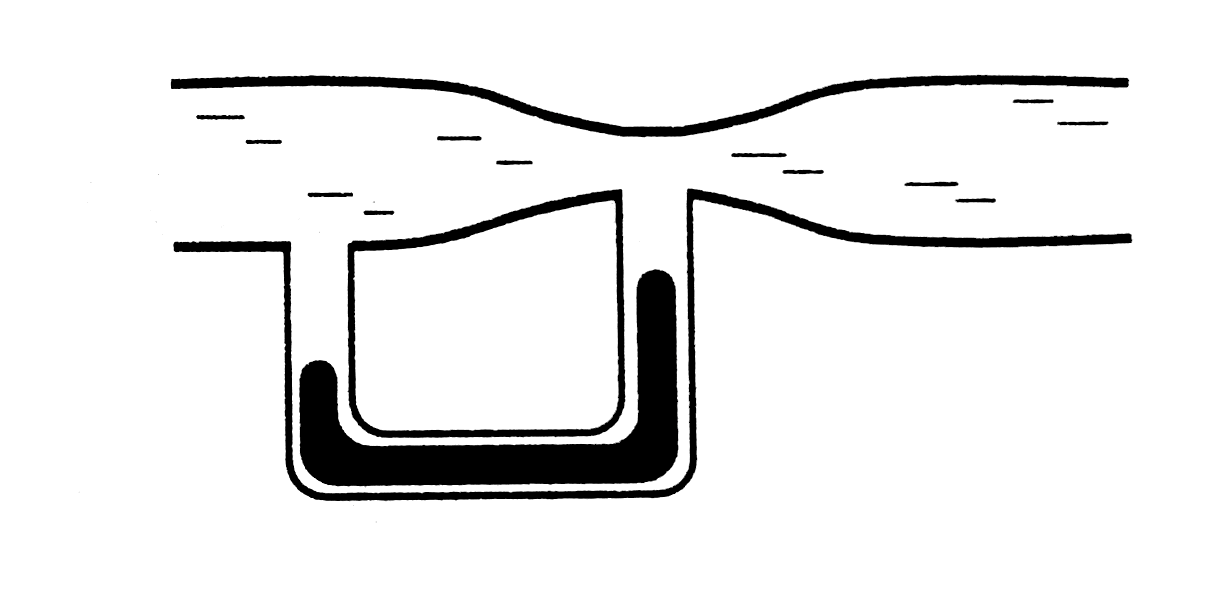
View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are 5cm2 and 2cm2 respectively. The rate of flow of water through the tube is 500cm3/s. Find the difference of mercury levels in the U-tube.
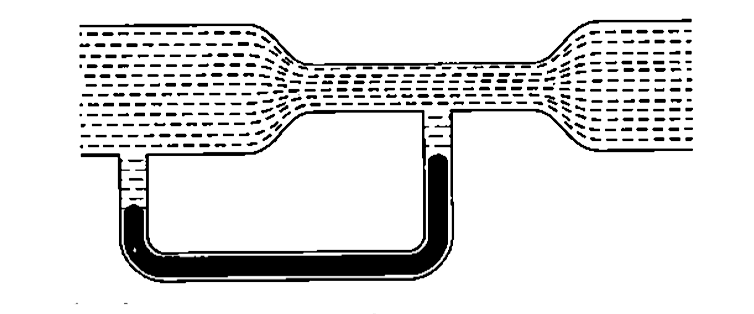
View SolutionWaster flows throgh a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find a the speed at B and b the difference in pressures at A and B.

View Solution
