Water from a tap emerges vertically downwards with an initial speed of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15m below the tap is
5.0×10−4m2
1.0×10−4m2
5.0×10−5m2
2.0×10−5m2
The correct Answer is:C
From conservation of energy
v22=v21+2gh …(i)
[ can also be found by applying Bernouli's theorem]
From continuity equation
A1v1=A2v2
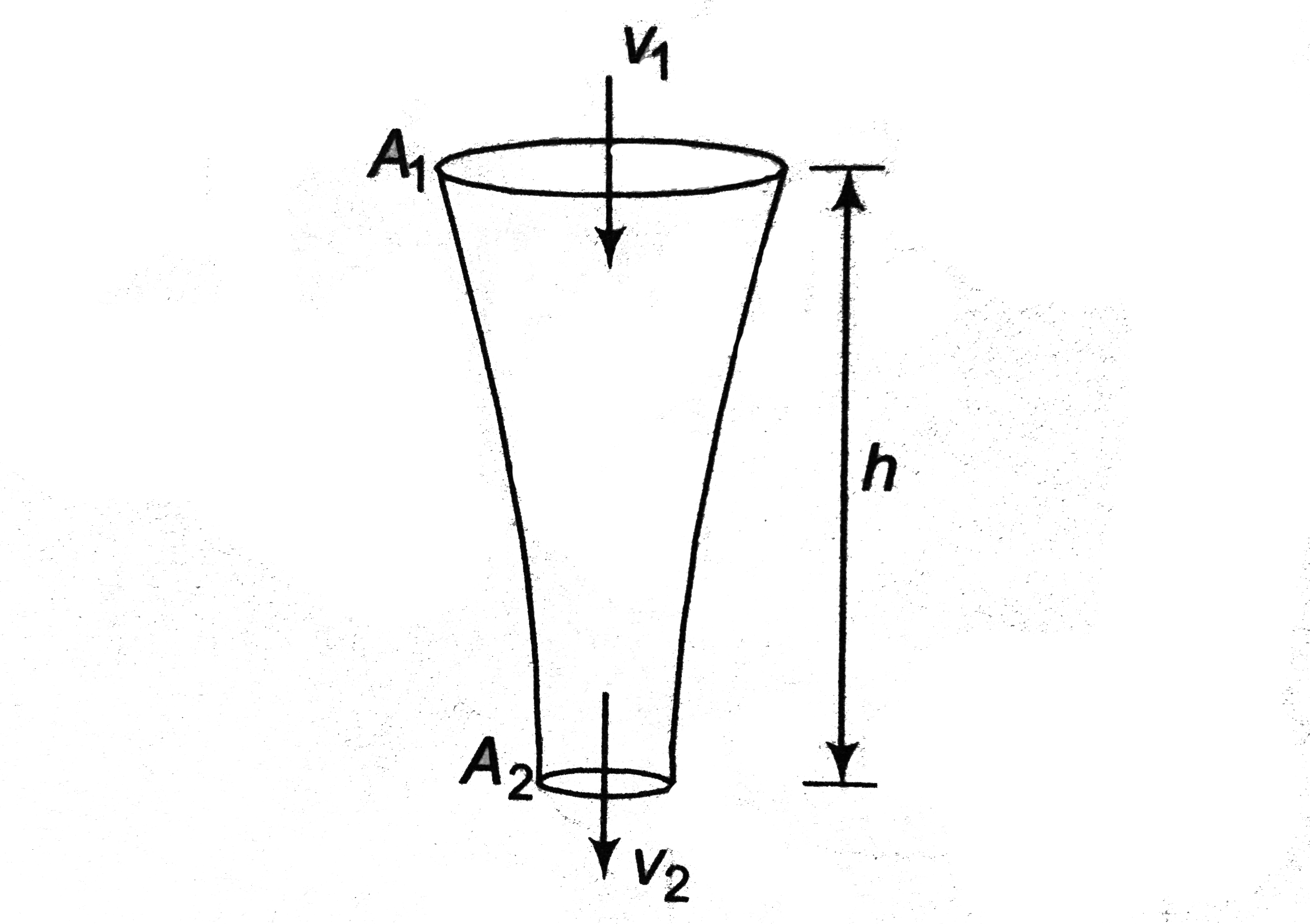
Substituting value of v2 from Eq. (ii) in eq. (i).
A21A22⋅v21=v21+2gh
or, A22A21v21v21+2gh
∴A2=A1v1√v21+2gh
Substituting the given values, we get
A2=(104)(1.0)√(1.0)2+2(10)(0.15)
A2=5.0×10−5m2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.5
3 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.6
4 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.3
4 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Water from a tap emerges vertically downwards an intial speed of 1 m/s . The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is contant throughout the stream of water and that the flow is steady . The cross-sectional area of the steam. 0.15 m below the tap is
View SolutionWater from a tap emerges vertically downward with an initial speed of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the flow is steady. What is the cross-sectional area of the stream 0.15 m below the tap? Use g=10ms−2.
View Solution
Knowledge Check
Water from a tap emerges vertically downward with an initial speed of 3.0 m/s. The cross-sectional area of the tap is 10−4m2 . Assume that the pressure is constant throughout the stream of water and that the flow is steady. The cross-sectional area of the stream 2 m below the tap is:
A0.7×10−5m2B10−4m2C4.3×10−5m2D2.8×10−5m2Water from a tap emerges vertically downwards with iitial velocity 4ms−1. The cross-sectional area of the tap is A. The flow is steady and pressure is constant thorughout the stream of water. The distance h vertically below the tap, where the cross-sectional area of the stream becomes (23)A is (g=10m/s2)
A0.5 mB1 mC1.5 mD2.2 mWater from a tap emerges vertically downwards with an initial velocity V0. Assume pressure is constant throughout the stream of water and the flow is steady. Find the distance form the tap at which cross-sectional area of stream is half of the cross-sectional area of stream at the tap.
AV20/2gB3V20/2gC2V20/2gD5V20/2g
In the previous question, at the mouth of the tap the area of cross-section is 2.5cm2 and the speed of water in 3m/s. The area of cross-section of the water column 80cm below the tap is.
View SolutionAt the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionA piston of cross-sectional area 100cm2 is used in a hydraulic pressure to exert a force of 107 dyne on the water. The cross-sectional area of the other piston which support a truck of mass 2000 kg is
View SolutionWater from a tap of cross sectional area 1cm2 starts falling down vertically, with a speed of 1m/s. What is the area of cross section of the stream of water at a distance of 20cm below the mouth of the tap?
[Assume that (1) the flow is steady, (2) pressure is constant throughout the stream of water and g=10m/s2]
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the tube where the cross sectional area is 10−2(m2), the water velcity is 2m/s and the pressure is 8000Pa. The pressure of water at another point where cross sectional area is 0.5×(10)−2(m2) is
View Solution
