Water is flowing through a horizontal pipe whose one end is closed with a valve. Initially the pressure recorded by pressure gauge ia 4×105N/m2. On opening the valve, the pressure gauge records 2×105N/m. Find the speed of water flowing through the pipe.
The correct Answer is:20 m/s
To find the speed of water flowing through the pipe after the valve is opened, we can use Bernoulli's equation. Let's go through the solution step by step.
Step 1: Understand the Initial Conditions
Initially, when the valve is closed, the pressure in the pipe is given as:
- P1=4×105N/m2
- The velocity of water, V1=0m/s (since the water is not flowing).
Step 2: Understand the Conditions After Opening the Valve
After opening the valve, the pressure in the pipe changes to:
- P2=2×105N/m2
- The velocity of water, V2 (which we need to find).
Step 3: Apply Bernoulli's Equation
Bernoulli's equation states that for an incompressible, non-viscous fluid flowing in a streamline, the following holds:
12ρV21+P1+ρgh1=12ρV22+P2+ρgh2
Since the pipe is horizontal, the heights h1 and h2 are the same, thus they cancel out. We can simplify the equation to:
P1+12ρV21=P2+12ρV22
Step 4: Substitute Known Values
Substituting the known values into the equation:
- V1=0
- P1=4×105N/m2
- P2=2×105N/m2
- Density of water, ρ=1000kg/m3
The equation becomes:
4×105+0=2×105+12×1000×V22
Step 5: Rearranging the Equation
Rearranging gives:
4×105−2×105=12×1000×V22
2×105=12×1000×V22
Step 6: Solve for V22
Multiplying both sides by 2:
4×105=1000×V22
Dividing both sides by 1000:
V22=4×1051000=400
Step 7: Calculate V2
Taking the square root:
V2=√400=20m/s
Final Answer
The speed of water flowing through the pipe after the valve is opened is:
20m/s
---
Initially, when the valve is closed, the pressure in the pipe is given as:
- P1=4×105N/m2
- The velocity of water, V1=0m/s (since the water is not flowing).
After opening the valve, the pressure in the pipe changes to:
- P2=2×105N/m2
- The velocity of water, V2 (which we need to find).
Bernoulli's equation states that for an incompressible, non-viscous fluid flowing in a streamline, the following holds:
12ρV21+P1+ρgh1=12ρV22+P2+ρgh2
Since the pipe is horizontal, the heights h1 and h2 are the same, thus they cancel out. We can simplify the equation to:
P1+12ρV21=P2+12ρV22
Substituting the known values into the equation:
- V1=0
- P1=4×105N/m2
- P2=2×105N/m2
- Density of water, ρ=1000kg/m3
4×105+0=2×105+12×1000×V22
Rearranging gives:
4×105−2×105=12×1000×V22
2×105=12×1000×V22
Multiplying both sides by 2:
4×105=1000×V22
Dividing both sides by 1000:
V22=4×1051000=400
Taking the square root:
V2=√400=20m/s
The speed of water flowing through the pipe after the valve is opened is:
20m/s
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions29videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Problems9videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
Water flows in a horizontal pipe whose one end is closed with a value and the pressure gauge falls to 1×105N/m2 when the value is opend. Calculate the speed of water flowing in the pipe.
View SolutionThe reading of pressure meter attached with a closed pipe is 3.5×105Nm−2. On opening the value of the pipe, the reading of the pressure meter is reduced to 3.0×105Nm−2. Calculate the speed of the water flowing in the pipe.
View Solution
Knowledge Check
- Question 1 - Select One
The reading of a pressure gauge attached to a closed horizontal pipe was 3.5×105 Pa. When the valve of the pipe was opened , the pressure was reduced to 3×105 Pa. What was the speed of water flowing out of the pipe ?
A2.5 m/sB5 m/sC7.5 m/sD10 m/s - Question 2 - Select One
One end of a horizontal pipe is closed with the help of a velve and the reading of a barometer attached in the pipe is 3×105 pascal When the value in the pipe is opened then the reading of barometer falls to 105 pascal the velocity of water flowing through the pipe will be in m/s-
A0.2B2C20D200
A pressure meter when attached with a closed horizontal pipe shows a reading of 5×105 N/m2. When the valve of the pipe is opened, the reading of the pressure meter falls to 3.5×105N/m2. Determine the speed of the water flowing in the pipe.
View SolutionWater is flowing through two horizontal pipes of different diameters which are connected together. In the first pipe the speed of water 4 m/s and the pressure is 2.0×104N/m2. Calculate the speed and pressure of water in the second pipe. The diameter of the pipes the diameter of the pipes are 3 cm and 6 cm respectively.
View SolutionConsider a horizontal water pipe connected to a pressure meter. When the pipe is closed the pressure displayed is 4.5×105Nm−2 and when the pipe is openekd the pressure displayed is 4×105Nm−2. Then what is the speed of the water (in standard units) flowing in the pipe ?
View SolutionWater is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is 4×104N/m2 at a point where cross-section is 0.02m2 and velocity of flow is 2m/s. What is the pressure at a point where cross-section reduces to 0.01m2 ?
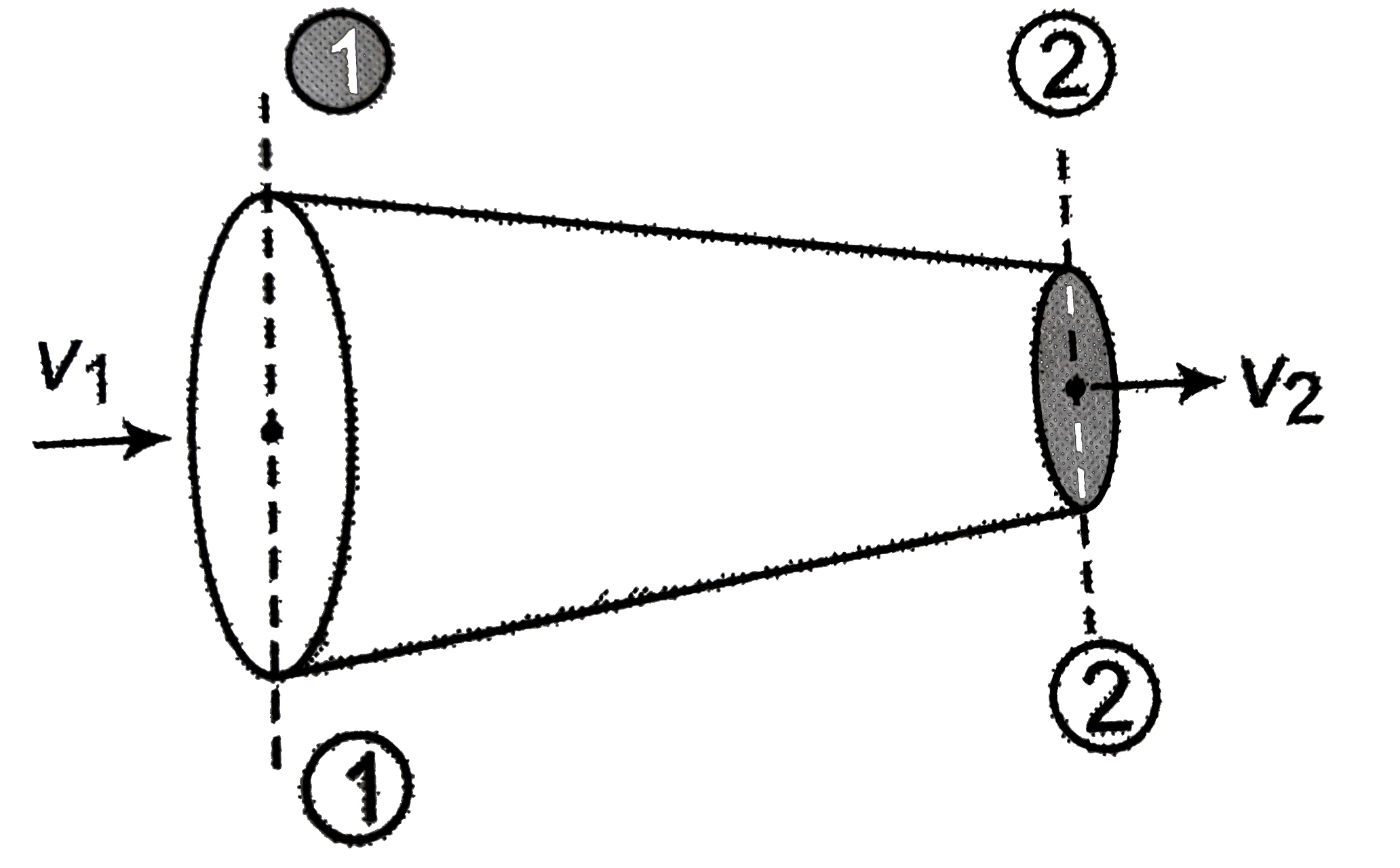 .View Solution
.View SolutionA manometer connected to a closed tap reads 4.2×106Nm2 and when tap is opened the readin of manometer falls to 4.0×106Nm2 . Find the speed of flow of water.
View SolutionThe pressure at the bottom of a lake due to water is 4.9×106N/m2. What is the depth of the lake?
View Solution

