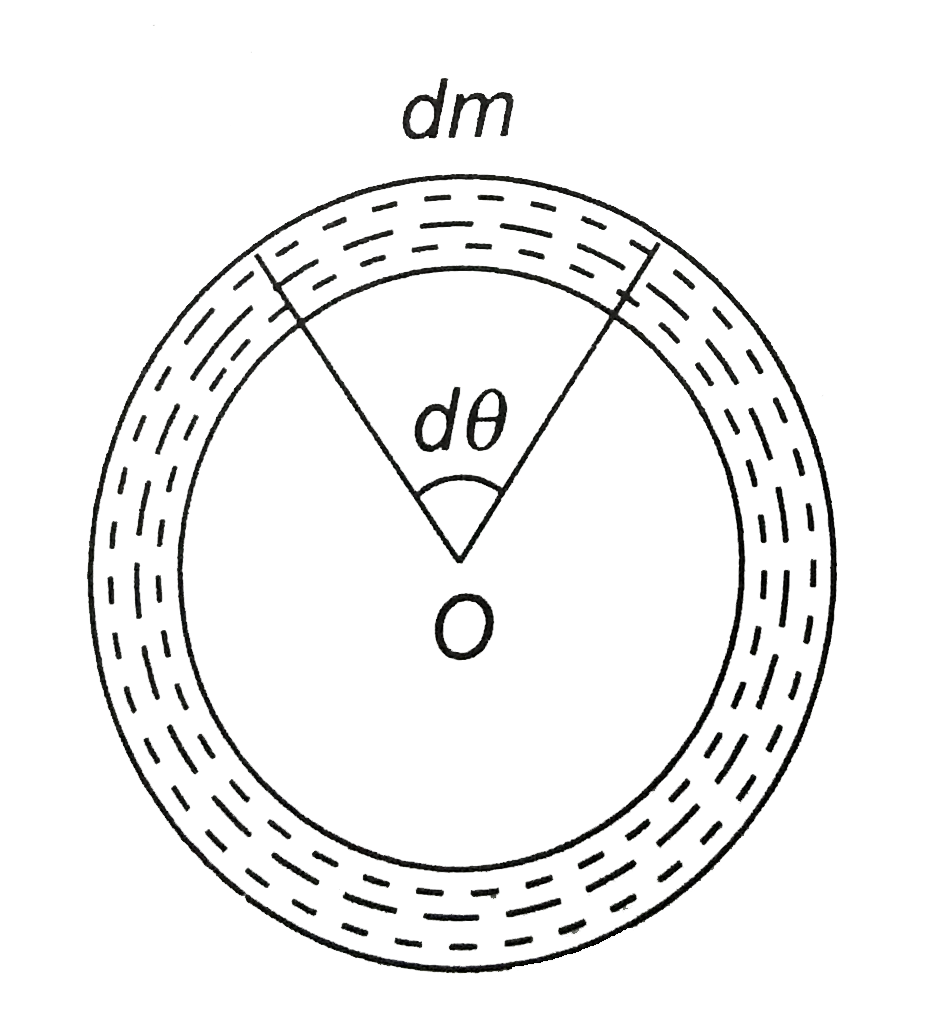
Water of density p flows with a linear speed v through a horizontal rubber tube having the form of a ring of radius R. If the diameter of the tube is d(<<R), find the tension in the rubber tube.
Mass of water contained in length subtending angle dθ at center
dl=−Rdθ
dm=ρπr2dl=rhaoπ(d2)2Rdθ=πρd2R4dθ
radial component of tension provides centripetal force.
2Tsin(dθ2)=dmv2R
2Tdθ2=πρd2R4v2Rdθ
T=(πρd2v24
(as dθ is small, sin(dθ)2=dθ2)

Topper's Solved these Questions
Similar Questions
Water is flowing through a long horizontal tube. Let PAandPB be the pressures at two points A and B of the tube
View SolutionUnder a constant pressure head, the rate of streamlined volume flow of a liquid through a capillary tube is V. if the length of the capillary tube is double and diameter of the bore is halved, find the rate of flow of the liquid through the capillary tube.
View Solution
Knowledge Check
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
When two capillary tubes through which the liquid is flowing are joined in series then the equivalent liquid resistance isARs=R1+R2BRs=R1−R2C1Rs=1R1+1R2DKηpr=1R1−1R2When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
πpr48ηl is dimensionally equivalent to (R is the resistance)Ap/RBp/R2Cp/R3Dp/RWhen a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
The dimensional formula for rate of flowAMLT−2BM0L3T−1CMLT−1DML2T−3
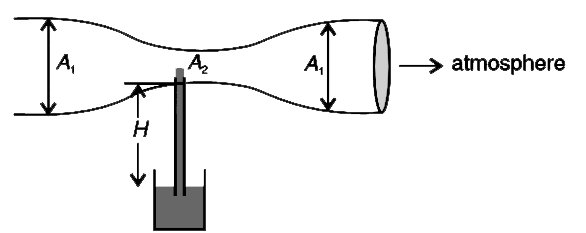
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
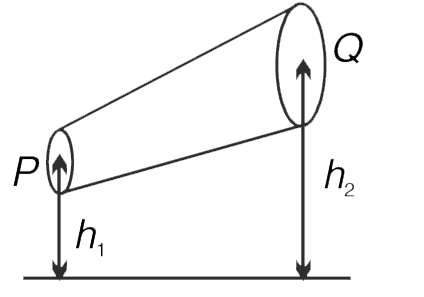
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View SolutionFind the nature of flow of water flowing at a speed of 8cms−1 through a horizontal tube of radius 2 cm. The viscosity of water at room temperature is 0.01 Poise.
View SolutionThe value of end correction for the pipe open at both the ends is a
(If the d is the inner diameter of the tube and r is the radius of the tube .)
View Solution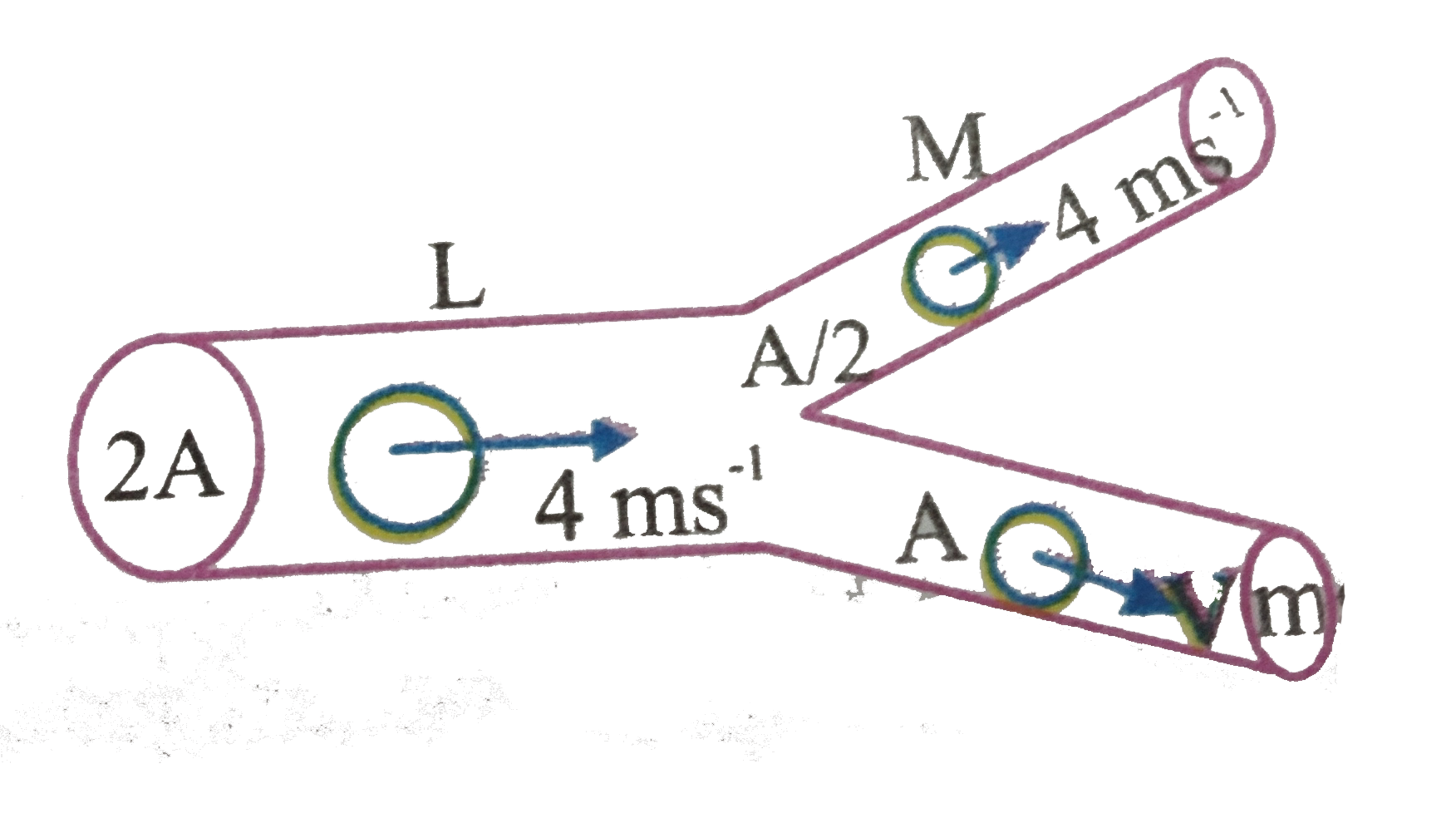
An incompressible liquid flows through a horizontal tube LMN as shown in the figure. Then the velocity V of the liquid throught he tube N is:
View SolutionWater is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 cm and 6 cm respectively. If the speed of water in the narrower tube is 4ms−1. Then the speed of water in the wider tube is
View Solution