Water stands at a depth behind the vertical upstream face of a dam as shown in the figure. The force exerted on the dam by water per unit width is

The correct Answer is:B
Step by step video, text & image solution for Water stands at a depth D behind the vertical upstream face of a dam as shown in the figure. The force exerted on the dam by water per unit width is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Level 1 Subjective
Explore 36 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Subjective Question
Explore 2 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Assertion and Reason
Explore 1 Video
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
In Fig ., the fresh water stands at depth D = 30.0 m behind the vertical upstream face of a dam of width W = 250 m. Find (a) the net horizontal force on the dam from the gauge pressure of the water and (b) the net torque due to that force about a horizontal line through O parallel to the (long) width of the dam. This torque tends to rotate the dam around that line, which would cause the dam to fail. (c) Find the moment arm of the torque.

View SolutionWater stands at a depth h behind the vertical face of a dam. It exerts a resultant horizontal force on the dam tendibg to slide it along its foundation and a torque tending to overturn the dam about the point O. Find

(a) Horizontal force,(b) torque about O, (c ) the height at which the resultant force would have to act to produce the same torque,l=cross-sectional length and ρ=density of water.
View Solution
Knowledge Check
Water stands upto a height h behind the vertical wall of a dam what is the net horizontal force pushing the dam down by the stream if width of the dam is σ? (ρ= density of water)
A2hσgBh2σρg2Ch2σρg4Dhσρg4Water rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opend again. The length of the eater column remaining in the tube will be
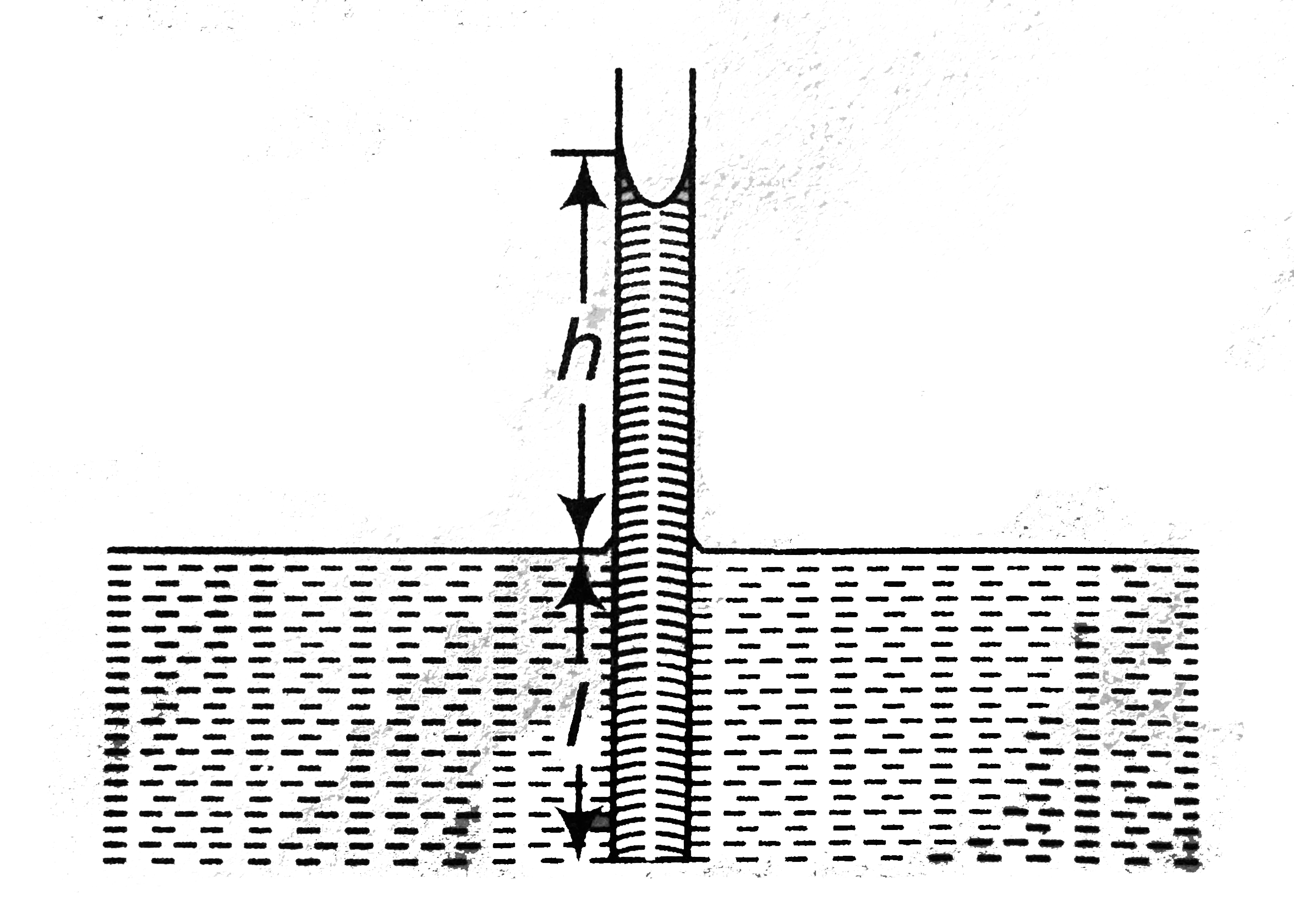 .A2hifl≥h and l+h if l≤hBhifl≥h and l+hifl≤hC4hifl≥h and l−hifl≤hDh2ifl≥h and l+hifl≤h
.A2hifl≥h and l+h if l≤hBhifl≥h and l+hifl≤hC4hifl≥h and l−hifl≤hDh2ifl≥h and l+hifl≤hA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA∣∣2P0Rh+πR2ρgh−2RT∣∣B∣∣2P0Rh+Rρgh2−2RT∣∣C∣∣P0πR2+Rρgh2−2RT∣∣D∣∣P0πR2+Rρgh2−2RT∣∣
A cube of side a and mass on just floats on the surface of water as shown in the figure. The surface tension and density of water are T and ρw respectively. If angle of contact between cube and water surface is zero, find the distance h (in metres) between the lower face of cube and surface of the water.
(Take m=1kg,g=10ms−12,aT=104 unit and ρwa2g=10 unit)

View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View SolutionA water tank stands on the roof of a building as shown in the figure. Then the value of h in m for which the distance covered by the water 'x' is greatest is
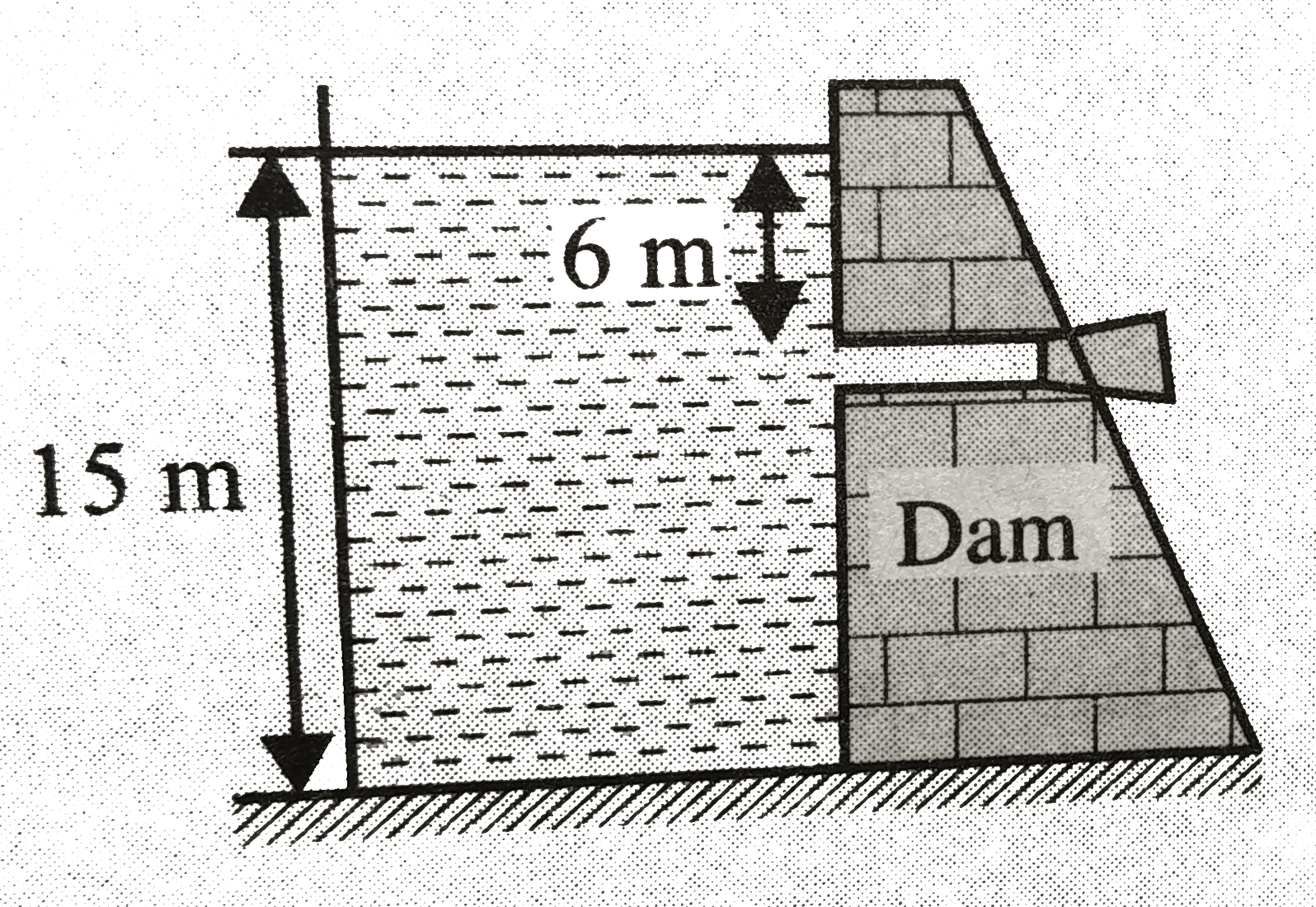
View SolutionWater stands at a depth of 15m behind a reservoir dam. A horizontal pipe 4cm in diameter passes through the dam 6m below the surface of water as shown. There is a plug which secures the pipe opening. Then find the friction between the plug and pipe wall.
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is

View Solution