We may define electrostatic potential at a point in an electrostatic field as the amount of work done in moving a unit positive test charge from infinity to that point against the electrostatic forces, along any path. Due to a single charge q , potential at a point distant r from the charge is V=q4π∈0r. The potential can be positive or negative. However, it is scalar quantity. The total amount of work done in bringing various charges to their respective postions from infinelty large mutual separations gives us the electric potential energy of the system of charges. Whereas electric potentail is measured in volt, electric potential energy is measured in joule. You are given a square of each side 1.0 metre with four charges +1×10−8C,−2×10−8C,+3×10−8C and +2×10−8C placed at the four corners of the square. With the help of the passage given above, choose the most approprite alternative for each of the following questions :
Potential energy fo the system of four system of four charges is
12.73×107J
−6.4×107J
12.73×10−9J
−12.73×10−9J
The correct Answer is:B
To find the potential energy of the system of four charges placed at the corners of a square, we will follow these steps:
Step 1: Identify the Charges and Their Positions
We have four charges located at the corners of a square with side length 1 meter:
- Charge q1=+1×10−8C at (0, 0)
- Charge q2=−2×10−8C at (1, 0)
- Charge q3=+3×10−8C at (1, 1)
- Charge q4=+2×10−8C at (0, 1)
Step 2: Calculate the Potential Energy Between Each Pair of Charges
The potential energy U between two point charges qi and qj separated by a distance r is given by the formula:
Uij=kqiqjr
where k=14πϵ0≈9×109N⋅m2/C2.
Step 3: Calculate Pairwise Potential Energies
1. Between q1 and q2:
U12=k(1×10−8)(−2×10−8)1=−2×10−16k
2. Between q1 and q3:
U13=k(1×10−8)(3×10−8)1=3×10−16k
3. Between q1 and q4:
U14=k(1×10−8)(2×10−8)1=2×10−16k
4. Between q2 and q3:
U23=k(−2×10−8)(3×10−8)1=−6×10−16k
5. Between q2 and q4:
U24=k(−2×10−8)(2×10−8)1=−8×10−16k
6. Between q3 and q4:
U34=k(3×10−8)(2×10−8)1=6×10−16k
Step 4: Sum All Potential Energies
Now we sum all the potential energies calculated:
Utotal=U12+U13+U14+U23+U24+U34
Substituting the values:
Utotal=(−2+3+2−6−8+6)×10−16k
Utotal=(−5)×10−16k
Step 5: Substitute k and Calculate
Substituting k=9×109:
Utotal=−5×10−16×9×109=−4.5×10−6J
Step 6: Final Answer
The potential energy of the system of four charges is:
Utotal=−4.5×10−6J
We have four charges located at the corners of a square with side length 1 meter:
- Charge q1=+1×10−8C at (0, 0)
- Charge q2=−2×10−8C at (1, 0)
- Charge q3=+3×10−8C at (1, 1)
- Charge q4=+2×10−8C at (0, 1)
The potential energy U between two point charges qi and qj separated by a distance r is given by the formula:
Uij=kqiqjr
where k=14πϵ0≈9×109N⋅m2/C2.
1. Between q1 and q2:
U12=k(1×10−8)(−2×10−8)1=−2×10−16k
U13=k(1×10−8)(3×10−8)1=3×10−16k
U14=k(1×10−8)(2×10−8)1=2×10−16k
U23=k(−2×10−8)(3×10−8)1=−6×10−16k
U24=k(−2×10−8)(2×10−8)1=−8×10−16k
U34=k(3×10−8)(2×10−8)1=6×10−16k
Now we sum all the potential energies calculated:
Utotal=U12+U13+U14+U23+U24+U34
Substituting the values:
Utotal=(−2+3+2−6−8+6)×10−16k
Utotal=(−5)×10−16k
Substituting k=9×109:
Utotal=−5×10−16×9×109=−4.5×10−6J
The potential energy of the system of four charges is:
Utotal=−4.5×10−6J
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - MULTIPLE CHOICE QUESTIONS
5 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
The electrical potential at point in an electric field is 6 V. Find the work done in bringing 12 C of charge from infinity to that point.
View SolutionWhich among the following statements is true about the work done in bringing a unit positive charge from point P to Q in an electrostatic field ?
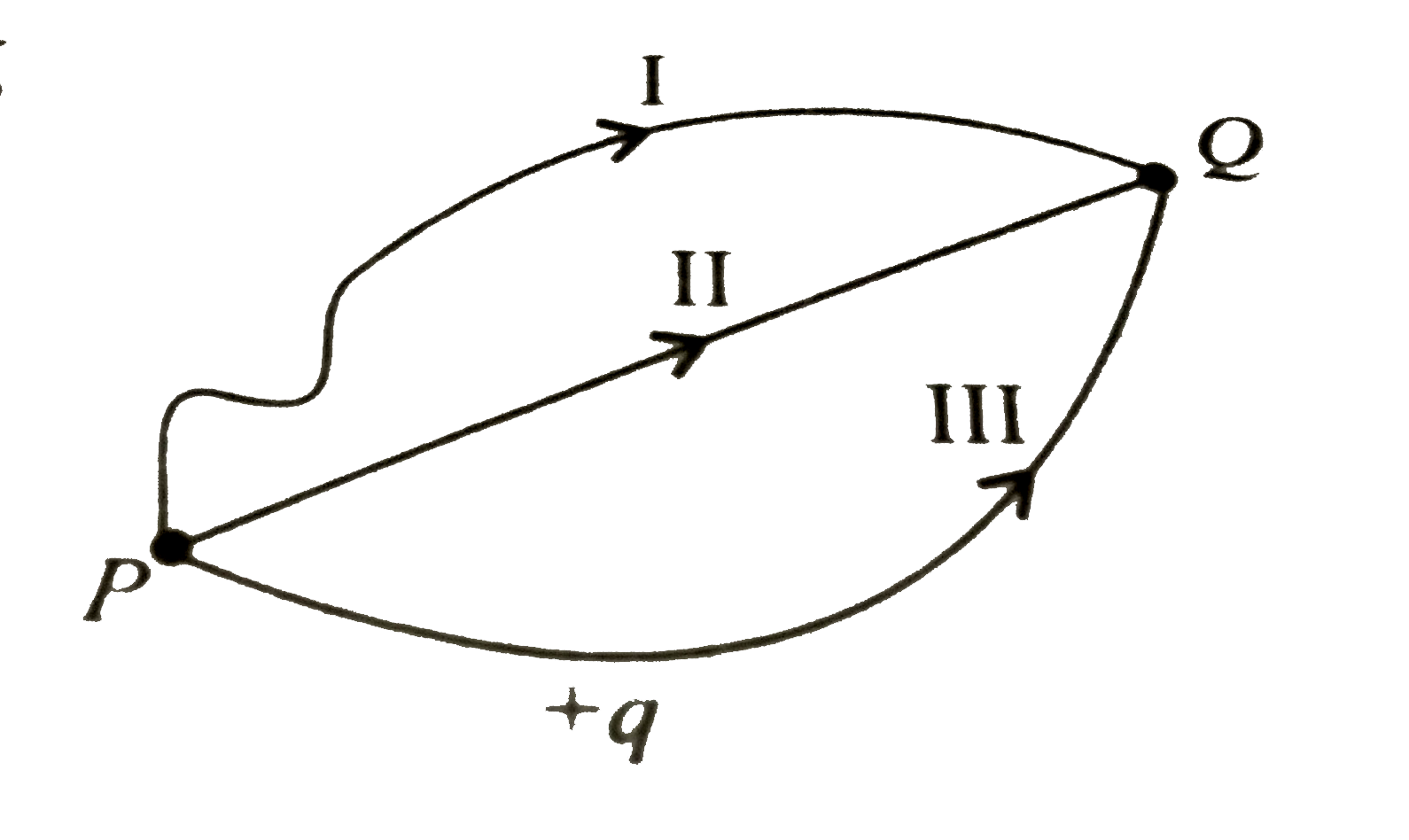
View Solution
Knowledge Check
We may define electrostatic potential at a point in an electrostatic field as the amount of work done in moving a unit positive test charge from infinity to that point against the electrostatic forces, along any path. Due to a single charge q , potential at a point distant r from the charge is V=q4π∈0r. The potential can be positive or negative. However, it is scalar quantity. The total amount of work done in bringing various charges to their respective postions from infinelty large mutual separations gives us the electric potential energy of the system of charges. Whereas electric potentail is measured in volt, electric potential energy is measured in joule. You are given a square of each side 1.0 metre with four charges +1×10−8C,−2×10−8C,+3×10−8C and +2×10−8C placed at the four corners of the square. With the help of the passage given above, choose the most approprite alternative for each of the following questions :
Electric potentail and electric potential energyAboth are scalarsBboth are vectorsCelectric potential is scalar and electric potential energy is vector,Delectric potentail is vector and electric potential energy is scalar.What is the work done in moving a unit positive charge from infinity to that point in electric field called?
AElectric potentialBPotential differenceCElectric currentDElectric circuitsThe work done in bringing a unit positive charge from infinity to the given point against the direction of electric intensity is
Aelectric potentialBmagnetic potentialCgravitational potentialDnone of these
Potential difference between any two points B and A in an electrostatic field is the amount of work done in carrying ………… from …………. to ………………….. .
View SolutionElectrostatic potentail V at point, distant r from a charge q varies as
View SolutionWork done (by the external force) per unit positive test charge in bringing it from infinity to the point is negative, for
View SolutionIf 6W is the work done in bringing a infinitesimal small test charge 6g from infinity to a point P, then potential at point P is
View SolutionThe work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
View Solution
