What are dimensions of physical quantities ? How do we represent them?
Step-by-Step Solution
1. Understanding Physical Quantities:
- Physical quantities are measurable quantities that can be quantified. Examples include speed, mass, length, time, etc.
Hint: Think of physical quantities as anything that can be measured or quantified in the physical world.
2. Example of a Physical Quantity:
- Consider speed as a measurable quantity. If we say an object is moving at a speed of 30, we need to specify the unit to understand what this means. For instance, is it 30 meters per second or 30 kilometers per hour?
Hint: Always remember that a number alone does not convey complete information without its unit.
3. Importance of Units:
- Units provide context to the numerical value. For example, "30 m/s" indicates a specific speed, while "30" alone is ambiguous. The units help us compare and understand the magnitude of the quantity.
Hint: Units are essential for clarity and understanding in measurements.
4. Representation of Dimensions:
- Dimensions of physical quantities are expressed in terms of the fundamental quantities: mass (M), length (L), and time (T). For example, speed can be represented dimensionally as length per unit time, which can be written as (L)(T−1).
Hint: Remember that dimensions are expressed in terms of fundamental quantities raised to certain powers.
5. Defining Dimensions:
- The formal definition of dimensions is: "Dimensions of physical quantities are the powers to which the units of mass, length, and time are raised to represent a physical quantity."
Hint: This definition emphasizes the relationship between physical quantities and their fundamental dimensions.
6. Difference Between Units and Dimensions:
- Units are specific measures (like meters, seconds, kilograms), while dimensions are the abstract representation of these measures (like (L) for length, (T) for time). For example, speed can be expressed in different units (m/s or km/h) but has the same dimension (L)(T−1).
Hint: Units can vary, but dimensions remain constant for a given physical quantity.
Summary
- Physical quantities are measurable and require units for clarity.
- Dimensions are expressed in terms of fundamental quantities (M, L, T).
- The representation of a physical quantity in terms of its dimensions helps in understanding its nature and comparison.
- Physical quantities are measurable quantities that can be quantified. Examples include speed, mass, length, time, etc.
- Consider speed as a measurable quantity. If we say an object is moving at a speed of 30, we need to specify the unit to understand what this means. For instance, is it 30 meters per second or 30 kilometers per hour?
- Units provide context to the numerical value. For example, "30 m/s" indicates a specific speed, while "30" alone is ambiguous. The units help us compare and understand the magnitude of the quantity.
- Dimensions of physical quantities are expressed in terms of the fundamental quantities: mass (M), length (L), and time (T). For example, speed can be represented dimensionally as length per unit time, which can be written as (L)(T−1).
- The formal definition of dimensions is: "Dimensions of physical quantities are the powers to which the units of mass, length, and time are raised to represent a physical quantity."
- Units are specific measures (like meters, seconds, kilograms), while dimensions are the abstract representation of these measures (like (L) for length, (T) for time). For example, speed can be expressed in different units (m/s or km/h) but has the same dimension (L)(T−1).
- Physical quantities are measurable and require units for clarity.
- Dimensions are expressed in terms of fundamental quantities (M, L, T).
- The representation of a physical quantity in terms of its dimensions helps in understanding its nature and comparison.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:REVISION EXERCISES (ADDITIONAL QUESTIONS)
Explore 4 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:REVISION EXERCISES (FILL IN THE BLANKS)
Explore 8 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
Explore 4 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
Knowledge Check
What physical quantities may X and Y represent ?
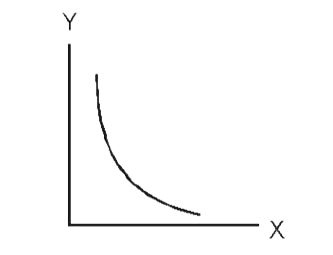 Apressure v/s temperature of a given gas (constant volume)Bkinetic energy v/s velocity of a particleCcapacitance v/s charge at a constant potentialDpotential v/s capacitance at a constant charge
Apressure v/s temperature of a given gas (constant volume)Bkinetic energy v/s velocity of a particleCcapacitance v/s charge at a constant potentialDpotential v/s capacitance at a constant chargeWhat physical quantities may X and Y represent?
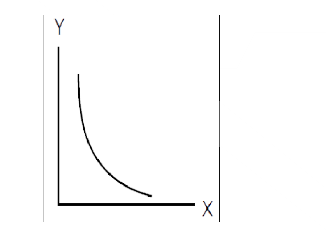 Apressure v/s temperature of a given gas (constant volume)Bkinetic energy v/s velocity of a particleCcapacitance v/s charge at a constant potentialDpotential v/s capacitance at a constant charge
Apressure v/s temperature of a given gas (constant volume)Bkinetic energy v/s velocity of a particleCcapacitance v/s charge at a constant potentialDpotential v/s capacitance at a constant chargePairs of physical quantities having same dimensions are
AReynolds number and strainBTorque and forceCCurie and frequencyDGravitational potential and latent heat
Dimension Formula for Physical Quantities
View SolutionWhat do you mean by physical quantities?
View SolutionWhat do you mean by dimensions of a physical quantity? Explain with the help of an example.
View SolutionIn Column-I, some physical quantities are given and in column-II, dimensions of the physical quantities are given . Match the entries in column-I to each entry in Column-II.

View SolutionIf the dimensions of a physical quantity are given by MaLbTc, then the physical quantity will be :
View Solution
