What are the advantages of the nll-point method in a Wheatstone bridge ? What additional measurements would be required to calculate Runknown by any other method ?
To solve the problem, we will break it down into two parts: the advantages of the null-point method in a Wheatstone bridge and the additional measurements required to calculate the unknown resistance using other methods.
1. Definition of Null Point: In a Wheatstone bridge, the null point is achieved when the potential difference between the two midpoints (where the galvanometer is connected) is zero. This means that no current flows through the galvanometer.
2. No Current Flow: At the null point, since the galvanometer shows zero deflection, the current through it is zero. This implies that the resistance of the galvanometer does not affect the circuit.
3. Energy Conservation: Because there is no current flowing through the galvanometer, there is no energy consumed by it. This is advantageous as it allows for more accurate measurements without energy loss.
4. Simplified Calculations: The balance condition of the Wheatstone bridge can be expressed as:
R1Runknown=R2R3
This relationship allows for easy calculation of the unknown resistance without needing to know the current or voltage in the circuit.
5. Increased Accuracy: The null-point method provides a more accurate measurement of the unknown resistance because it eliminates the effects of the galvanometer's resistance and any potential errors due to current flow.
Part 2: Additional Measurements Required for Other Methods
1. Using Kirchhoff’s Laws: If we were to calculate the unknown resistance using Kirchhoff’s Voltage Law (KVL) or Kirchhoff’s Current Law (KCL), we would need to measure the following:
- Currents in the Circuit: We would need to measure the currents flowing through each arm of the Wheatstone bridge (I1, I2, and IG).
- Voltage Drops: We would need to measure the voltage drops across each resistor in the circuit to apply KVL.
2. Application of KVL: Using KVL, we would set up equations based on the voltage drops around the loops of the circuit. This would require knowledge of the resistances and the applied voltage.
3. Solving for Unknown Resistance: Once we have the current and voltage measurements, we can use Ohm's Law (V = IR) to find the unknown resistance based on the calculated currents and voltage drops.
Summary of the Solution
- The null-point method in a Wheatstone bridge has several advantages, including no current flow through the galvanometer, energy conservation, simplified calculations, and increased accuracy.
- To calculate the unknown resistance using other methods, additional measurements of currents and voltage drops are required, along with the application of Kirchhoff’s laws.
R1Runknown=R2R3
This relationship allows for easy calculation of the unknown resistance without needing to know the current or voltage in the circuit.
- Voltage Drops: We would need to measure the voltage drops across each resistor in the circuit to apply KVL.
- To calculate the unknown resistance using other methods, additional measurements of currents and voltage drops are required, along with the application of Kirchhoff’s laws.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - MCQs (More than one options)
5 Videos
- COMMUNICATION SYSTEMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - LONG ANSWER TYPE QUESTION
5 Videos
Similar Questions
Knowledge Check
What is the return type of a method that does not return any value?
AintBfloatCvoidDdouble
What is the condition for the error in measuring resistance on a Wheatstone bridge to be a minimum? How can it be achieved?
View SolutionWhat is the advantage of using a polygonal mirror with larger number of faces in Michelson method of measuring the speed of light ?
View SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
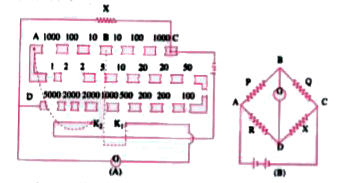
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method the necessary precaution to be taken is/are
View SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
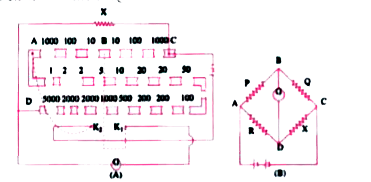
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method, height of the lower meniscus from free surface of water is 3cm while inner radius of capillary tubne is found to be 0.5cm. Then compute surface tension of water using this data. [Take contact angle between glass and water as 0° and g=9.8ms−2 ]
View SolutionHave you ever observed any water pollution in your area? What measures would you suggest to control it?
View Solution18g of glucose (molar mass 180gmol−1) is present in 500CM3 of its aqueous solution. What is the molarity of the solution? What additional data is required if the molality of the solution is also required to be calculated?
View SolutionThe molecular weights of sodium chloride and glucose are determined by the depression of freezing point method. As compared to their theoretical molecular weights, what will be their observed molecular weights when determined by the above method ? Justify your answer.
View Solution
