Question

What is simple pendulum? Deduce an expression for the time period of simple pendulum.

Explanation

Simple pendulum : ..A system of small massive body suspended by a light inexcusable and twice less string from a fixed (rigid) support is called a simple pendulum...
Whole mass of simple pendulum iks concentred on the centre of gravity of suspended body.
The distance from the point of suspension to the centre of mass of the bob is called length of pendulum.
An ideal pendulum is not possible but a simple pendulum as shown in figure can be taken in practice.

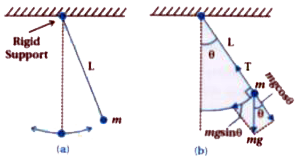
Derivation of expression for periodic time of simple pendulum : Consider simple pendulum a small bob of mass m tied to an inextansible massless string of length L.
The other end of the string is fixed to a support in the ceiling.
The bob oscillates in a plane about the vertical line through the support.
Let `theta` be the angle made by the string with the vertical.
There are two forces acting on the body :
(1) Tension T along the string
(2) Vertical force due to gravity = mg
The force mg can be resolved into two components.
(1) Parallel component `mg cos theta` which is redial component along string.
(2) Perpendicular components `mg sin theta` which is a tangential component.
The motion of the bob is along a circle of the length L and centre at the support point, the bob has a radial acceleration `(omega^(2)L)` and also a tangential acceleration. The resultant radial force is `T-mg cos theta` and tangential force is `mg sin theta`.
Torque is zero due to radial force because line of force passing through support point.
From `tau = rF sin theta`
Torque due to tangential force
`tau = -L(mg sin theta)" "".........."(1) [therefore tau = rF sin theta]`
This is a restoring torque that tends to reduce angular displacement hence the negative sign is there in formula.
By Newton.s law of rotational motion `(F= ma), tau = I alpha " ""..........."(2)`
Where I is the moment of inertia of the system about the support and `alpha` is the angular acceleration
From equation (1) and (2)
`I alpha = -L mg sin theta`
`therefore alpha= -(mg L)/(I).sin theta" ""........"(3)`
If `theta` is very small and in radian then
`sin theta= theta-(theta^3)/(3!)+(theta^5)/(5!)+"....."` [neglecting higher power terms]
`sin theta approx theta`
Equation (3) will be written as
`alpha = -(mgL)/(I)*theta" ""..........."(4)`
Here, `(mgL)/(I)=` constant
`therefore alpha oo - theta`
If in a linear motion `a propto -x` and this is condition of linear simple harmonic motion. Hence `alpha oo -theta`, is the condition for angular simple harmonic motion.
Hence, motion of simple pendulum is a simple harmonic motion.
Acceleration in a linear simple harmonic motion `a= -omega^(2)x`
From equation (4)
`omega^(2) = (mgL)/(I)`
`therefore omega = sqrt((mgL)/(I))`
`therefore (2pi)/(T) = sqrt((mgL)/(I))`
`therefore T = 2pi sqrt((I)/(mgL))`
is the periodic time of simple pendulum.
Since the string of simple pendulum is massless, the moment of interia I is simply `mL^(2)`, where m = mass of bob.
The period of a simple pendulum, `T = 2 pi sqrt((L)/(g))`
So for small oscillation period of a simple pendulum `T propto sqrt(L)` and inversely proportional to `T propto (1)/(sqrt(g))`. (Square root of gravitational acceleration of the place)
The period of simple pendulum does not depend on the kind of material.