What is the maximum rate at which energy is stored in inductor (L) when it is connected in series with resistance R and one battery of emf E and negligible internal resistance? Refer to growth and decay of current in a coil, explained in competition file.
To solve the problem of finding the maximum rate at which energy is stored in an inductor (L) when it is connected in series with a resistance (R) and a battery of emf (E) with negligible internal resistance, we can follow these steps:
1. Understand the Circuit:
The circuit consists of an inductor (L), a resistor (R), and a battery with emf (E). The inductor stores energy in the magnetic field when current flows through it.
2. Current Growth in the Inductor:
The current (I) in the circuit grows according to the formula:
I(t)=I0(1−e−t/τ)
where I0=ER is the maximum current, and τ=LR is the time constant.
3. Energy Stored in the Inductor:
The energy (U) stored in the inductor at any time t is given by:
U=12LI2
Substituting the expression for I:
U=12L(I0(1−e−t/τ))2
This expands to:
U=12L(ER)2(1−e−t/τ)2
4. Differentiate Energy to Find Power:
The power (P), which is the rate of change of energy, is given by:
P=dUdt
To differentiate U with respect to t, we apply the chain rule:
P=L(ER)2(1−e−t/τ)⋅ddt(1−e−t/τ)
The derivative of (1−e−t/τ) is:
1τe−t/τ
Therefore, substituting this into the power equation gives:
P=L(ER)2(1−e−t/τ)⋅1τe−t/τ
5. Maximize Power:
To find the maximum power, we set the derivative of P with respect to t equal to zero:
dPdt=0
This leads to the condition:
(1−e−t/τ)=e−t/τ
Solving this gives:
1=2e−t/τ⟹e−t/τ=12
6. Substituting Back to Find Maximum Power:
We substitute e−t/τ=12 back into the power equation:
Pmax=L(ER)2(1−12)⋅1τ⋅12
Simplifying gives:
Pmax=E24R
Final Result:
The maximum rate at which energy is stored in the inductor is:
E24R
The circuit consists of an inductor (L), a resistor (R), and a battery with emf (E). The inductor stores energy in the magnetic field when current flows through it.
The current (I) in the circuit grows according to the formula:
I(t)=I0(1−e−t/τ)
where I0=ER is the maximum current, and τ=LR is the time constant.
The energy (U) stored in the inductor at any time t is given by:
U=12LI2
Substituting the expression for I:
U=12L(I0(1−e−t/τ))2
This expands to:
U=12L(ER)2(1−e−t/τ)2
The power (P), which is the rate of change of energy, is given by:
P=dUdt
To differentiate U with respect to t, we apply the chain rule:
P=L(ER)2(1−e−t/τ)⋅ddt(1−e−t/τ)
The derivative of (1−e−t/τ) is:
1τe−t/τ
Therefore, substituting this into the power equation gives:
P=L(ER)2(1−e−t/τ)⋅1τe−t/τ
To find the maximum power, we set the derivative of P with respect to t equal to zero:
dPdt=0
This leads to the condition:
(1−e−t/τ)=e−t/τ
Solving this gives:
1=2e−t/τ⟹e−t/τ=12
We substitute e−t/τ=12 back into the power equation:
Pmax=L(ER)2(1−12)⋅1τ⋅12
Simplifying gives:
Pmax=E24R
The maximum rate at which energy is stored in the inductor is:
E24R
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE PROBLEMS25videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS22videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
Similar Questions
A potentiometer has a wire of 100cm length and its resistance is 10 Ohms.It is connected in series with a resistance of 40 ohms and a battery of emf 2V and negligible internal resistance.If a source of unknown emf E connected in the secondary is balanced by 40cm length of potentiometer wire the value of 'E' is
View SolutionAn inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View Solution
Knowledge Check
- Question 1 - Select One
A series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depeds upon
AL and R onlyBE and L onlyCE and R onlyDL,R and E only - Question 2 - Select One
AB is a potentiometer wire of length 100cm and its resistance is 10ohms. It is connected in series with a resistance R=10ohms and a battery of e.m.f. 2V and negligible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is
 A0.8VB1.6VC0.08VD0.16V
A0.8VB1.6VC0.08VD0.16V - Question 3 - Select One
AB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
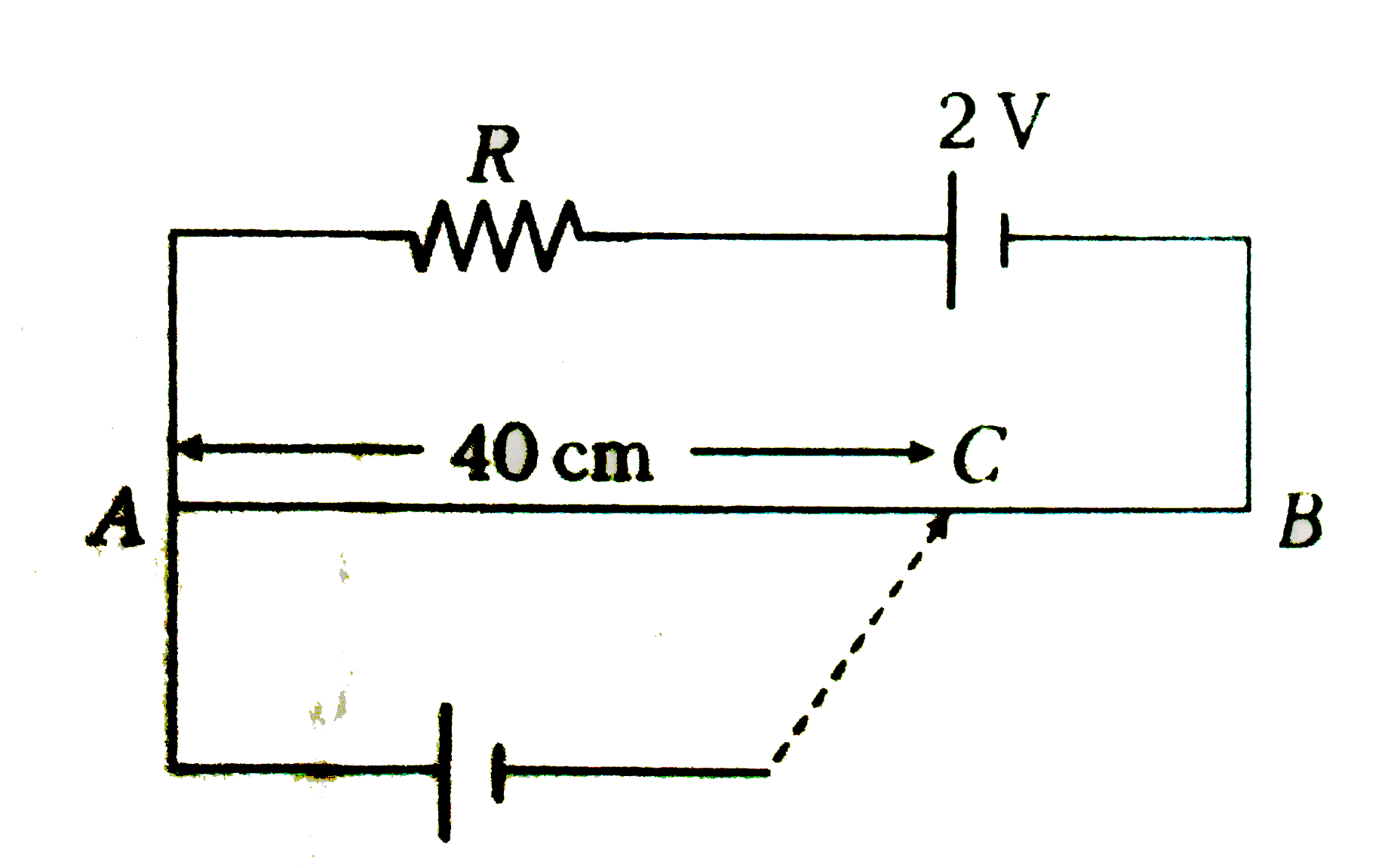 A0.8VB1.6VC0.08VD0.16V
A0.8VB1.6VC0.08VD0.16V
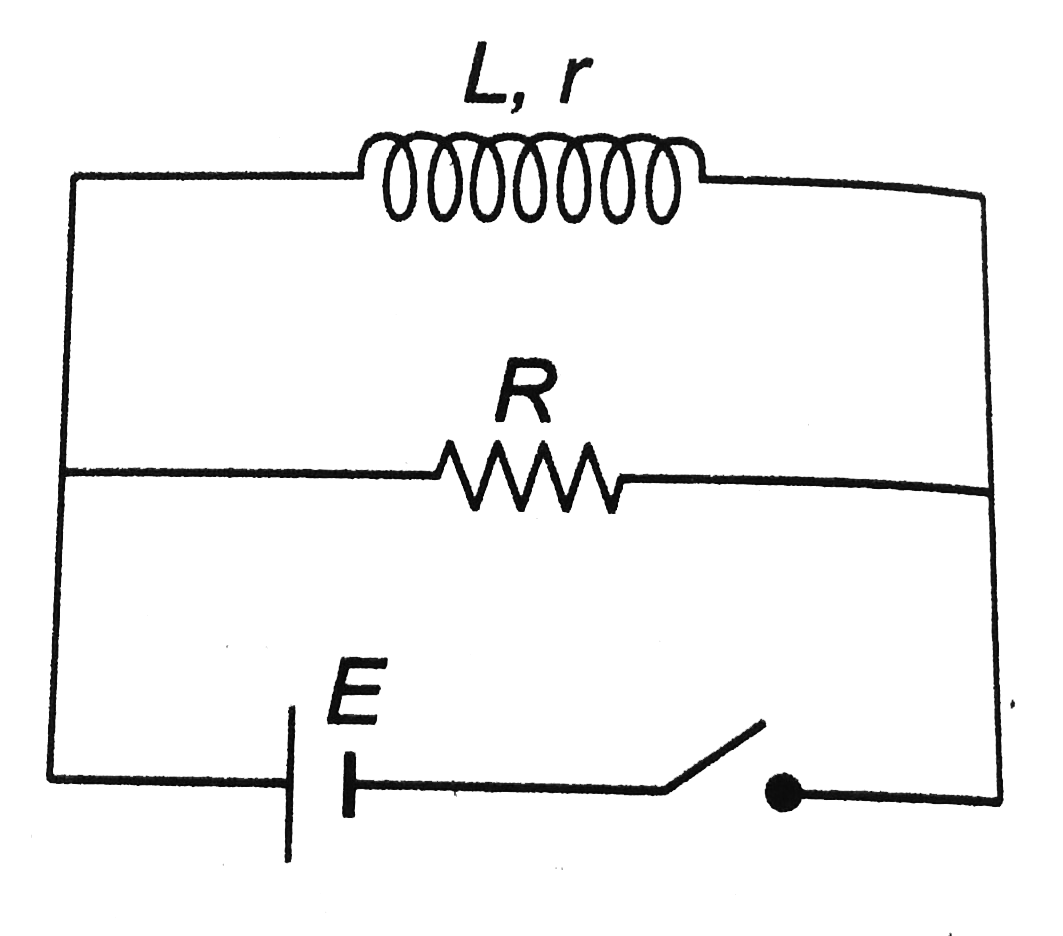
A solenoid of inductance L with resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time t=0, switch S is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
 View Solution
View SolutionA voltmeter of resistance RV and an ammeter of resistance RA are connected in series across a battery of emf E and of negligible internal resistance . When a resistance R is connected in parallel to volmeter , reading of ammeter increases to three times while that of volmeter reduces to one - third. Calculate RAandRV in terms of R.
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionShows a network of eight resistors battery of resistance R(=2Ω) connected in a 3V battery of negligible internal resistance. The current I in the circuit is
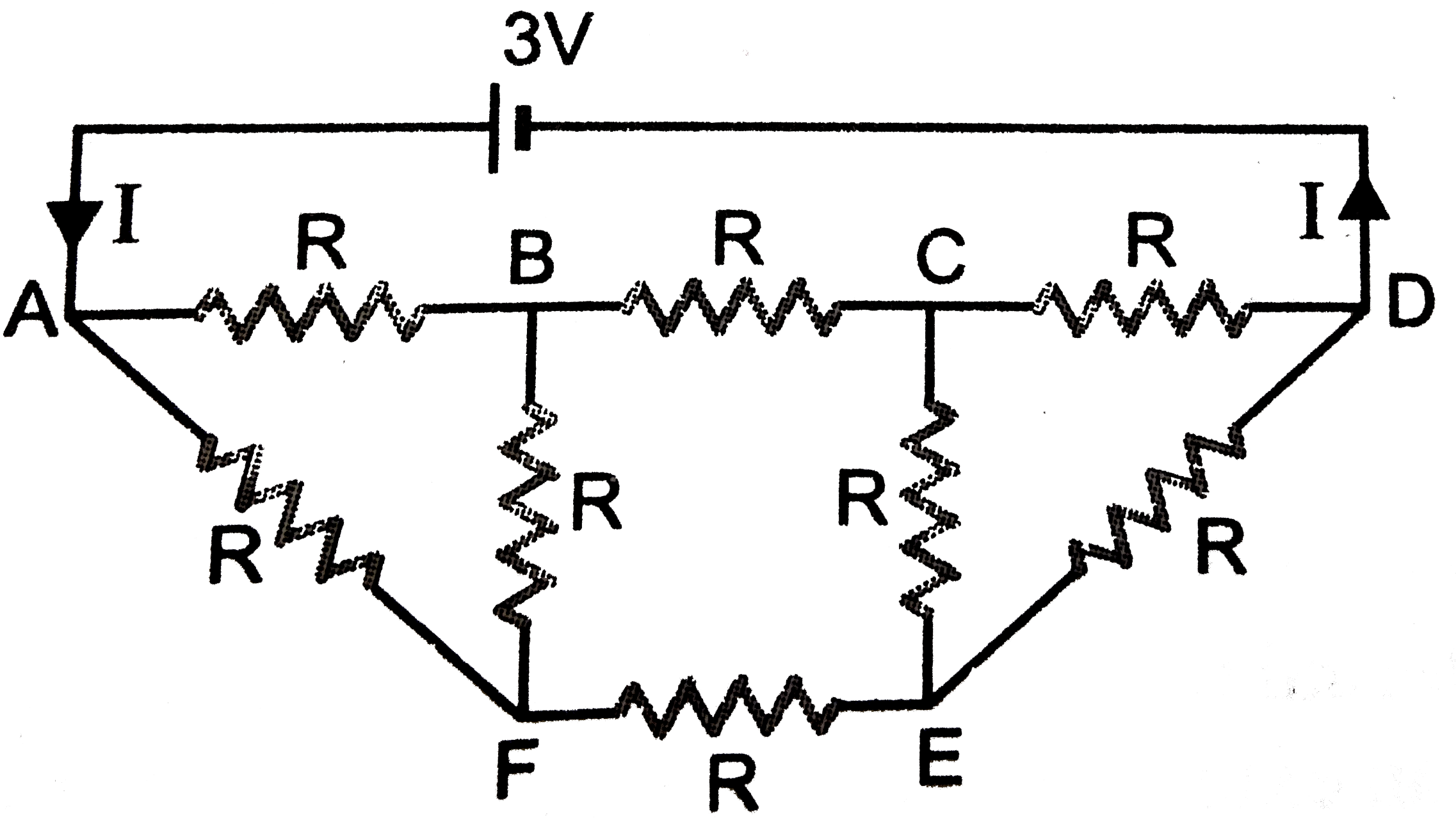 View Solution
View SolutionAn inductor coil and a capacitor and a resistance of 5Ω are connected in series to an a.c. source of rms voltage 30 V. When the frequency of the source is varied, a maximum r.m.s. current of 5 A is observed. If this inductor is connected in parallel with a resistance 5Ω to a battery of emf 25 V and internal resistance 2.0Ω, the current drawn from the battery is
View Solution

