What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
√2gR
√3gR
√5gR
√gR
The correct Answer is:C
To find the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop, we can follow these steps:
Step 1: Understand the Problem
We need to determine the minimum velocity at the bottom of the loop such that when the body reaches the top of the loop, it has just enough speed to maintain contact with the loop.
Step 2: Analyze Forces at the Top of the Loop
At the top of the loop, the forces acting on the body are:
- The gravitational force mg acting downward.
- The normal force N acting downward (which will be zero at the minimum velocity).
For the body to just maintain contact at the top of the loop, the centripetal force required to keep the body in circular motion must equal the gravitational force acting on it. Thus, we can write:
mg+N=mv2R
Setting N=0 (for the minimum velocity), we have:
mg=mv2R
This simplifies to:
v2=gR
Step 3: Apply Conservation of Energy
We will apply the work-energy theorem from the bottom of the loop to the top of the loop. The change in potential energy as the body moves from the bottom to the top is:
ΔPE=mg(2R)=2mgR
The change in kinetic energy is given by:
ΔKE=12mv2top−12mv2min
Step 4: Set Up the Energy Equation
Using the conservation of energy, we have:
ΔKE+ΔPE=0
Substituting the expressions we derived:
12mv2top−12mv2min+2mgR=0
Substituting v2top=gR into the equation:
12m(gR)−12mv2min+2mgR=0
This simplifies to:
12mgR−12mv2min+2mgR=0
Step 5: Solve for v2min
Combining terms, we get:
12mgR+2mgR=12mv2min
52mgR=12mv2min
Dividing both sides by 12m:
5gR=v2min
Thus, we find:
vmin=√5gR
Final Answer
The minimum velocity with which a body of mass m must enter a vertical loop of radius R to complete the loop is:
vmin=√5gR
We need to determine the minimum velocity at the bottom of the loop such that when the body reaches the top of the loop, it has just enough speed to maintain contact with the loop.
At the top of the loop, the forces acting on the body are:
- The gravitational force mg acting downward.
- The normal force N acting downward (which will be zero at the minimum velocity).
mg+N=mv2R
Setting N=0 (for the minimum velocity), we have:
mg=mv2R
This simplifies to:
v2=gR
We will apply the work-energy theorem from the bottom of the loop to the top of the loop. The change in potential energy as the body moves from the bottom to the top is:
ΔPE=mg(2R)=2mgR
The change in kinetic energy is given by:
ΔKE=12mv2top−12mv2min
Using the conservation of energy, we have:
ΔKE+ΔPE=0
Substituting the expressions we derived:
12mv2top−12mv2min+2mgR=0
Substituting v2top=gR into the equation:
12m(gR)−12mv2min+2mgR=0
This simplifies to:
12mgR−12mv2min+2mgR=0
Combining terms, we get:
12mgR+2mgR=12mv2min
52mgR=12mv2min
Dividing both sides by 12m:
5gR=v2min
Thus, we find:
vmin=√5gR
The minimum velocity with which a body of mass m must enter a vertical loop of radius R to complete the loop is:
vmin=√5gR
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns3videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A small body is tied to an end of an inextensible string of negligible mass and length r, the other end being clamped to a rigid support. What is the minimum velocity with which the body must be projected horizontally so that it can go completely round a vertical circle without slakening of the string at the highest point ?
View Solution………….. is the minimum velocity with which a body must be projected vertically upwards in order to escape earth's gravitational field.
View Solution
Knowledge Check
- Question 1 - Select One
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
A√gRB√2gRC√3gRD√5gR - Question 2 - Select One
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
A√gRB√2gRC√3gRD√2gR3gR - Question 3 - Select One
The adjoining figure represent a semi-circular loop of charge Q and of radius R .The minimum velocity with which a point mass mof charge −q should be projected so that it becoems free from the influence of the loop is
 A√2Qqπε0mRB√Qqπε0mRC√Qq2πε0mRD√Qq4πε0mR
A√2Qqπε0mRB√Qqπε0mRC√Qq2πε0mRD√Qq4πε0mR
What is the minimum speed required at the bottom to perform a vertical loop, if the radius of the death-well in a circus is 25m?
View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
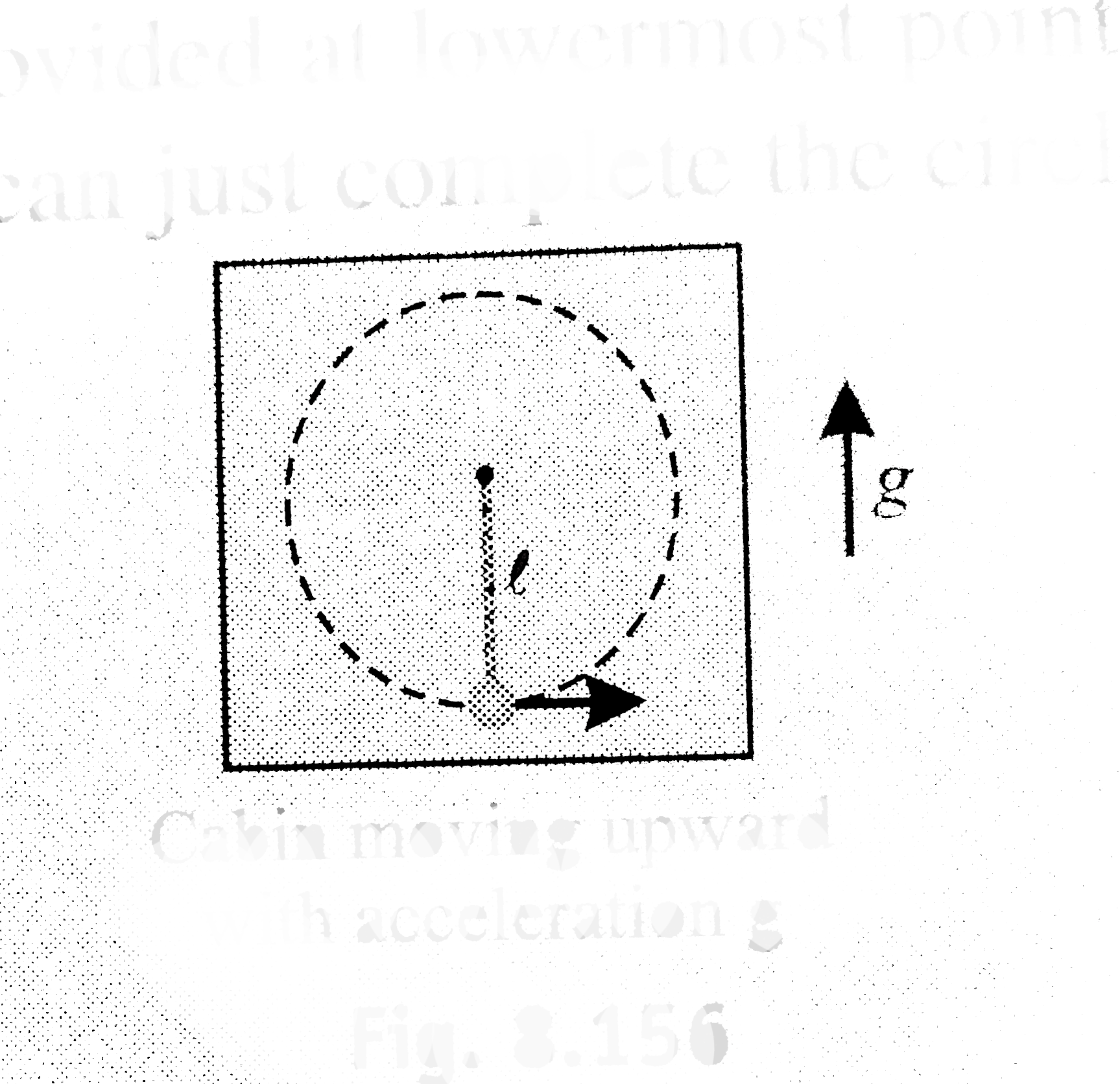 View Solution
View SolutionIn a loop ,a body starts at a height h =2R. The minimum speed with which the body must be pushed down initially in order that it may be able to complete the vertical circle is
View SolutionA small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
View SolutionAn inclined track ends in a circular loop of radius r. From what height on the track a particle should be released so that it completes the loop, assuming there is no friction ?
View Solution

