What reading would you expact of a square-wave current, suitching rapodly between +0.5 A and -0.5 A, when passed through an ac ammeter?
0
0.5A
0.25A
1.0A
The correct Answer is:B
To solve the problem of determining the reading of a square-wave current switching rapidly between +0.5 A and -0.5 A when passed through an AC ammeter, we can follow these steps:
1. Understanding the AC Ammeter:
- An AC ammeter measures the root mean square (RMS) value of the alternating current.
2. Defining the Square Wave Current:
- The square wave current alternates between +0.5 A and -0.5 A. This means that for half the time (T/2), the current is +0.5 A, and for the other half (T/2), it is -0.5 A.
3. Calculating the RMS Value:
- The RMS value of a current is defined as the square root of the average of the squares of the instantaneous values over one complete cycle.
- For a square wave, the formula for RMS current (I_rms) can be simplified as:
Irms=√1T∫T0I2(t)dt
4. Setting Up the Integral:
- We can break the integral into two parts:
- From 0 to T/2, where I = +0.5 A
- From T/2 to T, where I = -0.5 A
- Thus, the integral becomes:
Irms=
⎷1T(∫T/20(0.5)2dt+∫TT/2(−0.5)2dt)
5. Calculating Each Integral:
- For the first part (0 to T/2):
∫T/20(0.5)2dt=(0.5)2⋅T2=0.25⋅T2=0.125T
- For the second part (T/2 to T):
∫TT/2(−0.5)2dt=(−0.5)2⋅T2=0.25⋅T2=0.125T
6. Combining the Results:
- Now, we add the two results:
∫T0I2(t)dt=0.125T+0.125T=0.25T
7. Final Calculation of RMS Current:
- Plugging this back into the RMS formula:
Irms=√1T⋅0.25T=√0.25=0.5 A
8. Conclusion:
- The reading on the AC ammeter will be 0.5 A.
- An AC ammeter measures the root mean square (RMS) value of the alternating current.
- The square wave current alternates between +0.5 A and -0.5 A. This means that for half the time (T/2), the current is +0.5 A, and for the other half (T/2), it is -0.5 A.
- The RMS value of a current is defined as the square root of the average of the squares of the instantaneous values over one complete cycle.
- For a square wave, the formula for RMS current (I_rms) can be simplified as:
Irms=√1T∫T0I2(t)dt
- We can break the integral into two parts:
- From 0 to T/2, where I = +0.5 A
- From T/2 to T, where I = -0.5 A
- Thus, the integral becomes:
Irms=
⎷1T(∫T/20(0.5)2dt+∫TT/2(−0.5)2dt)
- For the first part (0 to T/2):
∫T/20(0.5)2dt=(0.5)2⋅T2=0.25⋅T2=0.125T
- For the second part (T/2 to T):
∫TT/2(−0.5)2dt=(−0.5)2⋅T2=0.25⋅T2=0.125T
- Now, we add the two results:
∫T0I2(t)dt=0.125T+0.125T=0.25T
- Plugging this back into the RMS formula:
Irms=√1T⋅0.25T=√0.25=0.5 A
- The reading on the AC ammeter will be 0.5 A.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct
5 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
An ac ammeter is used to measure currnet in a circuit. When a given direct current passes through the circuit. The ac ammeter reads 3 A. When another alternating current passes through the circuit, the ac ammeter reads 4A. Then find the reading of this ammeter (inA), if dc and ac flow through the circuit simultaneously.
View SolutionA dc ammeter and a hot wire ammeter are connected to a circuit in series. When a direct current is passed through circuit, the dc ammeter shows 6 A. When ac current flows through circuit, the ac ammeter shows 8A. What will be reading of each ammeter if dc and ac current flow simulataneously through the circuit?
View SolutionA moving coil galvanometer is converted into an ammeter reads upto 0.03A by connecting a shunt of resistance 4r across it and ammeter reads up 0.06A, when a shunt of resistance r is used. What is the maximum current which can be sent through this galvanometer if no shunt is used ?
View SolutionIn the circuit as shown if the current drawn through battery is 0.5A. Then
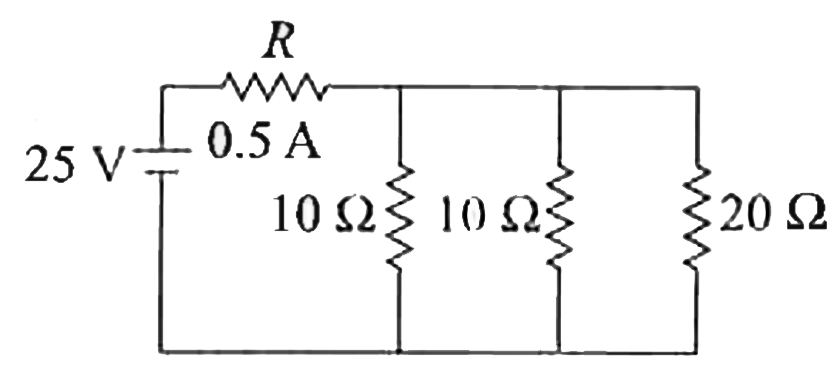
View SolutionA galvanometer having a coil resistance of 60Ω shows full scale defection when a current of 1.0A passes thoguth it. It can vbe convered into an ammeter to read currents up to 5.0A by
View SolutionA current of 1.5A flows through a conductor for 2.0s. What amount of charge passes through the conductor ?
View SolutionAn ammeter of resistance 1 Ohm can measure current upto 1.0 A. (i) What must be the value of the shunt resistance to enable the ammeter to measure upto 5.0 A? (ii) What is the combined resistance of the ammeter and the shunt?
View SolutionAn iron rod of volume 10−4m3 and relative permeability 1000 is placed inside a long solenoid wound with 5 turns/cm. If a current of 0.5A is passed through the solenoid, then the magnetic moment of the rod is
View SolutionAn iron rod of volume 10−4m3 and relative permeability 1000 is placed inside a long solenoid wound with 5turns/cm. If a current of 0.5A is passed through the solenoid, then the magnetic moment of the rod is
View SolutionA moving coil galvnometer is converted into an ammeter reading up to 0.03A by connecting a shunt of resistance r4. What is the maximum current which can be sent through this galvanometer if no shunt is used (here r=resistance of galvanometer)
View Solution
