What will be the molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules?
32R
52R
R
3R
The correct Answer is:B
To find the molar specific heat at constant volume (CV) of an ideal gas consisting of rigid diatomic molecules, we can follow these steps:
1. Understanding Degrees of Freedom:
- For a diatomic molecule, if it were not rigid, it would have 7 degrees of freedom: 3 translational, 2 rotational, and 2 vibrational.
- However, since we are considering rigid diatomic molecules, the vibrational degrees of freedom are not considered. Therefore, the total degrees of freedom (f) for rigid diatomic molecules is:
f=3 (translational)+2 (rotational)=5
2. Using the Formula for Molar Specific Heat at Constant Volume:
- The molar specific heat at constant volume (CV) is related to the degrees of freedom by the formula:
CV=f⋅R2
- Here, R is the universal gas constant.
3. Substituting the Degrees of Freedom:
- Now, substituting f=5 into the equation:
CV=5⋅R2
4. Final Expression:
- Therefore, the molar specific heat at constant volume for an ideal gas consisting of rigid diatomic molecules is:
CV=5R2
Conclusion:
The molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules is 5R2.
---
- For a diatomic molecule, if it were not rigid, it would have 7 degrees of freedom: 3 translational, 2 rotational, and 2 vibrational.
- However, since we are considering rigid diatomic molecules, the vibrational degrees of freedom are not considered. Therefore, the total degrees of freedom (f) for rigid diatomic molecules is:
f=3 (translational)+2 (rotational)=5
- The molar specific heat at constant volume (CV) is related to the degrees of freedom by the formula:
CV=f⋅R2
- Here, R is the universal gas constant.
- Now, substituting f=5 into the equation:
CV=5⋅R2
- Therefore, the molar specific heat at constant volume for an ideal gas consisting of rigid diatomic molecules is:
CV=5R2
The molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules is 5R2.
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)7videos
KINETIC THEORY OF GASES
- BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )1videos
KINEMATICS
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))2videos
LAWS OF MOTION
Similar Questions
The molar specific heat at constant pressure of monoatomic gas is
View SolutionDetermine the molar heat capacity of a polytropic process through which an ideal gas consisting of rigid diatomic molecules goes and in which the number of collisions between the molecules remains constant
(a) in a unit volume ,
(b) in the total volume of the gas.View Solution
Knowledge Check
- Question 1 - Select One
Molar specific heat at constant volume Cv for a monatomic gas is
A32RB52RC3RD2R - Question 2 - Select One
Graph for specific heat at constant volume for a monoatomic gas
A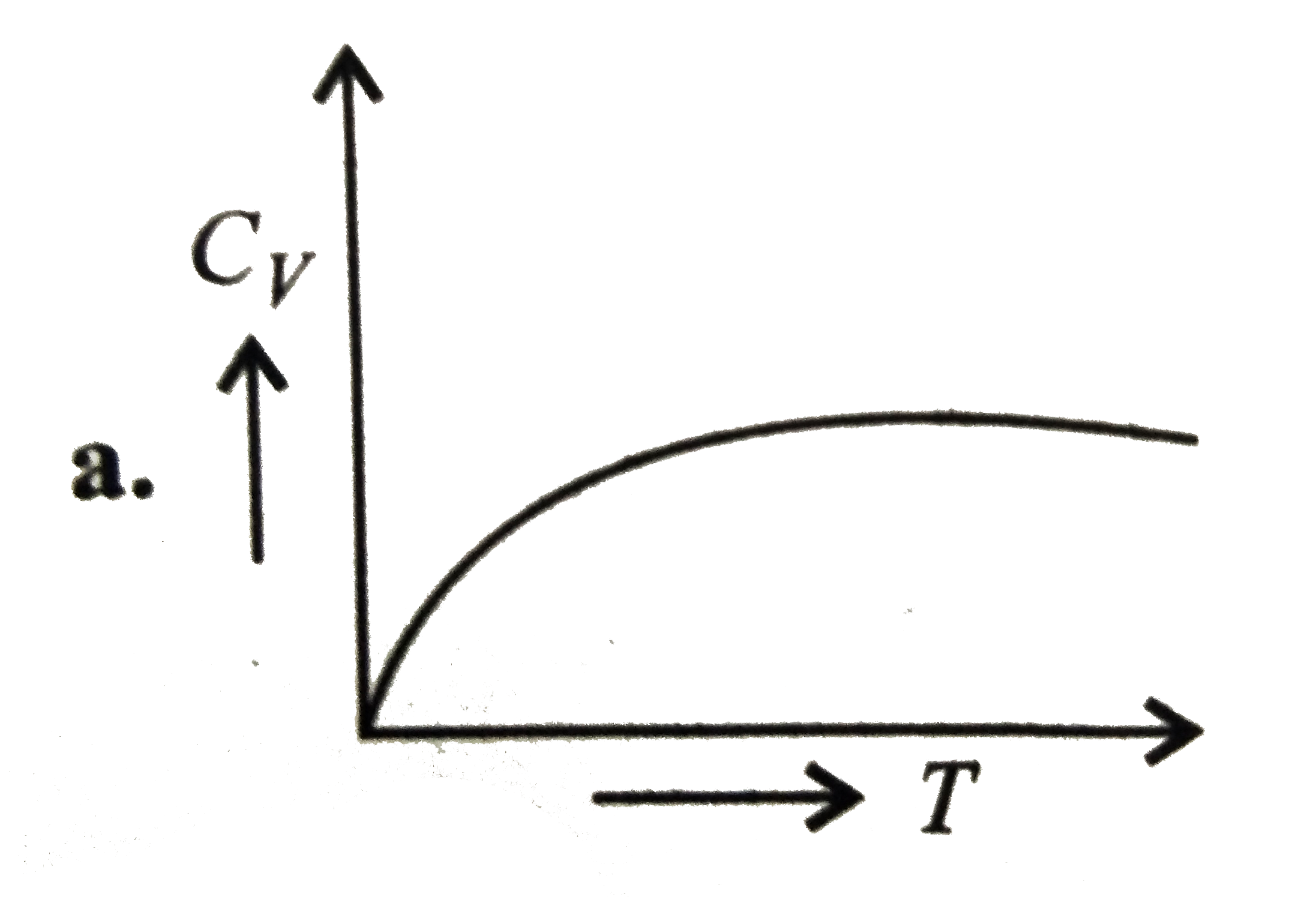 B
B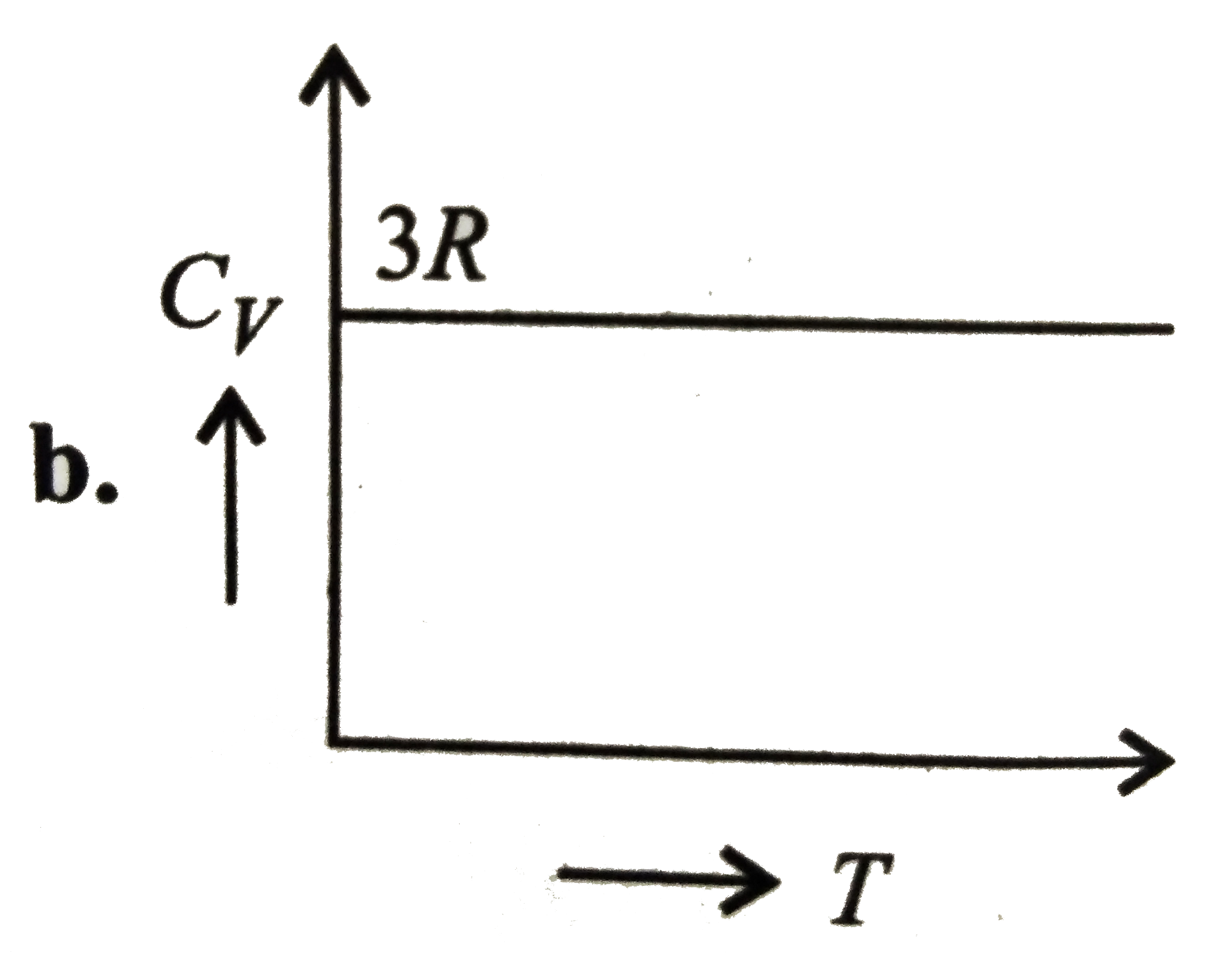 C
C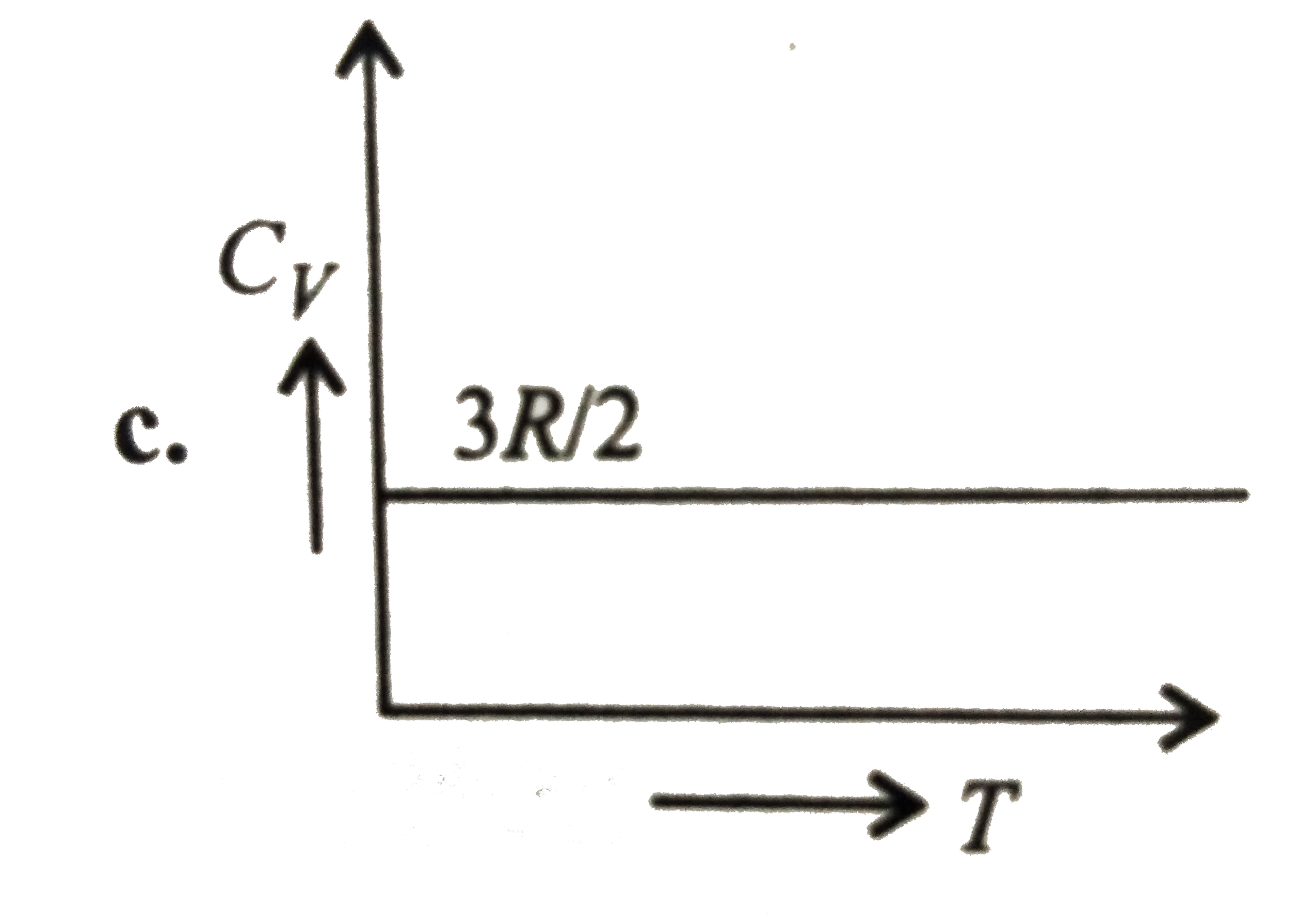 D
D - Question 3 - Select One
The molar specific heat at constant volume, for a non linear triatomic gas is
A3RB4RC2RDR
Calculate the molar specific heat at constant volume of neon gas. (R = 8.314 J mol−1K−1 )
View SolutionCalculate the molar specific heat at constant volume of neon gas.
(R=8.314J mol−1K−1)View SolutionGraph for specific heat at constant volume for a monoatomic gas
View SolutionThe molar specific heat at constant pressure of an ideal gas is 72R. The gas is made up of molecules which are
View SolutionIf the molar specific heat capacity at constant volume of an ideal gas is Cv=32R, then what is the corresponding molar specific heat capacity of the ideal gas at constant pressure ?
View Solution

