What work has to be done isobarically on a mole of diatomic gas to increase its rms speed η = 3 times from T0=300 K ?
To determine the work done isobarically on a mole of diatomic gas to increase its root mean square (rms) speed from an initial temperature T0=300K to a final speed that is three times the initial speed, we will follow these steps:
Step 1: Understand the relationship between rms speed and temperature
The rms speed vrms of a gas is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the temperature, and M is the molar mass of the gas.
Step 2: Set up the initial and final conditions
Let the initial rms speed be vrms1 at temperature T0=300K. The final rms speed vrms2 is three times the initial speed:
vrms2=3vrms1
Step 3: Relate the rms speeds to their respective temperatures
From the rms speed formula:
vrms1=√3RT0Mandvrms2=√3RT2M
Squaring both sides gives:
v2rms1=3RT0Mandv2rms2=3RT2M
Since vrms2=3vrms1, we have:
(3vrms1)2=9v2rms1=3RT2M
Step 4: Set up the equation for temperature
Equating the two expressions gives:
9(3RT0M)=3RT2M
This simplifies to:
9T0=T2
Substituting T0=300K:
T2=9×300=2700K
Step 5: Calculate the change in temperature
The change in temperature ΔT is:
ΔT=T2−T0=2700K−300K=2400K
Step 6: Calculate the work done isobarically
The work done W in an isobaric process is given by:
W=nRΔT
For one mole of gas (n=1) and using R=8.314J/(mol K):
W=1×8.314×2400
Calculating this gives:
W=19953.6J
Step 7: Convert to kilojoules
To convert to kilojoules:
W=19953.61000=19.95kJ
Final Answer
The work that has to be done isobarically on a mole of diatomic gas to increase its rms speed three times from T0=300K is approximately:
19.95kJ
The rms speed vrms of a gas is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the temperature, and M is the molar mass of the gas.
Let the initial rms speed be vrms1 at temperature T0=300K. The final rms speed vrms2 is three times the initial speed:
vrms2=3vrms1
From the rms speed formula:
vrms1=√3RT0Mandvrms2=√3RT2M
Squaring both sides gives:
v2rms1=3RT0Mandv2rms2=3RT2M
Since vrms2=3vrms1, we have:
(3vrms1)2=9v2rms1=3RT2M
Equating the two expressions gives:
9(3RT0M)=3RT2M
This simplifies to:
9T0=T2
Substituting T0=300K:
T2=9×300=2700K
The change in temperature ΔT is:
ΔT=T2−T0=2700K−300K=2400K
The work done W in an isobaric process is given by:
W=nRΔT
For one mole of gas (n=1) and using R=8.314J/(mol K):
W=1×8.314×2400
Calculating this gives:
W=19953.6J
To convert to kilojoules:
W=19953.61000=19.95kJ
The work that has to be done isobarically on a mole of diatomic gas to increase its rms speed three times from T0=300K is approximately:
19.95kJ
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.1
6 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.3
10 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Advance MCQs with One or More Options Correct
10 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
Knowledge Check
4 moles of an ideal monoatomic gas is heated isobarically so that its absolute temperature increases 2 times. Then the entropy increment of the gas in this process is
A285.J/kB42.5J/kC57.5J/kD76.5J/kThe work done by one mole of ideal gas when its teperature is increased by 1oC at constant pressure is
AR2B2RCRD4RFigure shows a cycle ABCDA undergone by 2 moles of an ideal diatomic gas. The curve AB is a rectangular hyperbola and T1=300K and T2=500K. Determine the work done by the gas in the process A→B.
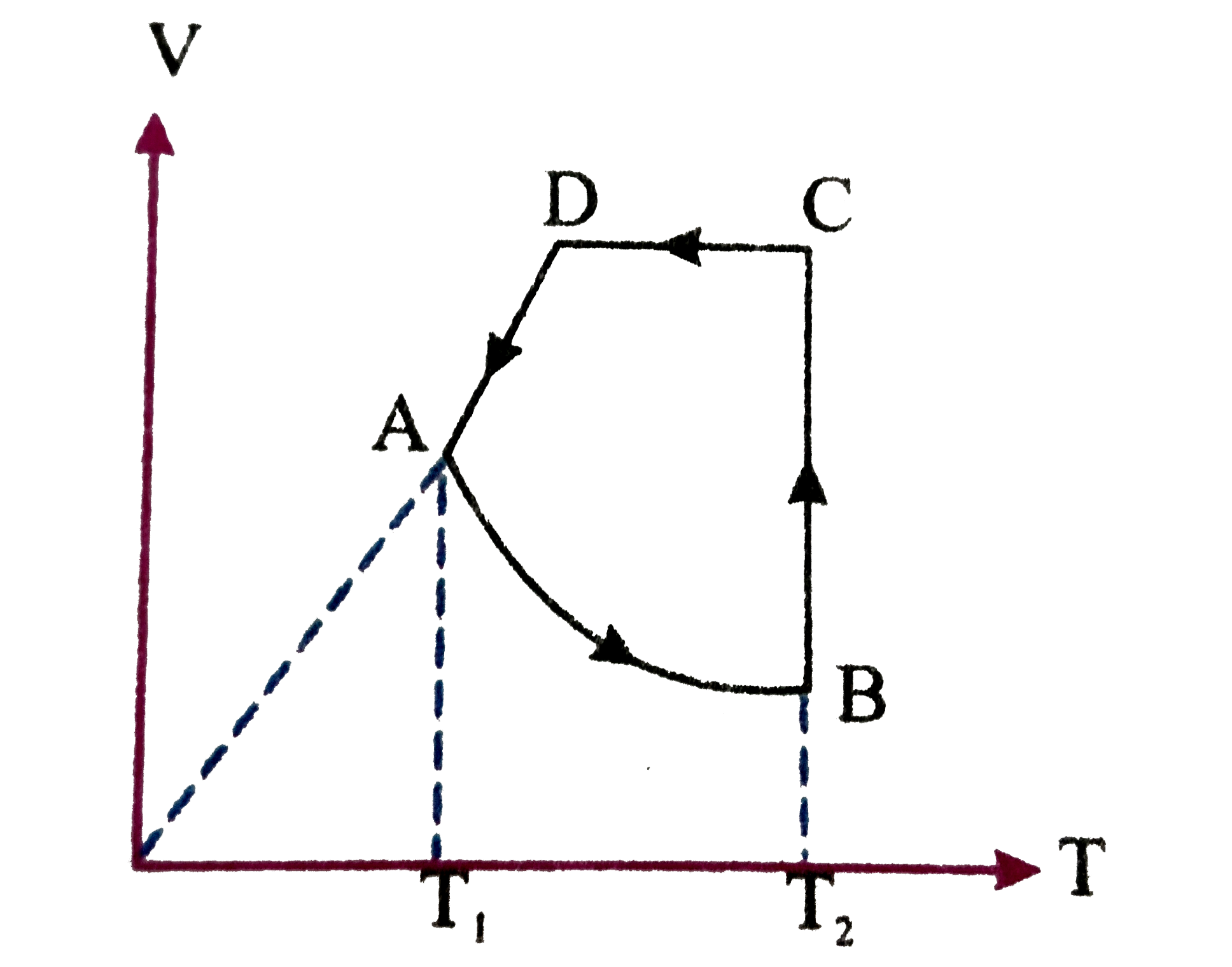 A−3.320kJB4.326kJC2.326kJD3.326kJ
A−3.320kJB4.326kJC2.326kJD3.326kJ
Temperature of 1 mole of an ideal gas is increased from 300K to 310K under isochoric process. Heat supplied to the gas in this process is Q=25R, where R=universal gas constant. What amount of work has to be done by the gas if temperature of the gas decreases from 310K to 300K adiabatically?
View SolutionOne mole of oxygen being initially at a temperature T0=290K is adiabatically compressed to increase its pressure η=10.0 times. Find :
(a) the gas temperature after the compression ,
(b) the work that has been performed on the gas.
View SolutionThe work done by one mole of ideal gas when its temperature is increased by1∘C at constant pressure is
View SolutionTwo moles of a diatomic gas at 300 K are kept in a nonconducting container enclosed by a piston . Gas is now compressed to increase the temperature from 300 K to 400 K. Find word done by the gas

View SolutionWhat is the work done by 0.2 mole of a gas at room temperature to double its volume during isobaric process? (Take R=2 cal mol−1.∘C−1)
View Solution
