When a boy is playing on a swing in the sitting position , the time period of oscillations of the swing is T. If the boy stands up , the time period of oscillation of the spring will be
more than T
less than T
equal to T
Cannot be predicted
The correct Answer is:B
To solve the problem, we need to analyze how the time period of oscillation of a swing changes when the boy goes from a sitting position to a standing position.
1. Understanding the Time Period of a Pendulum:
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- L is the length from the pivot point to the center of mass of the pendulum,
- g is the acceleration due to gravity.
2. Identifying the Initial Condition:
When the boy is sitting on the swing, the center of mass of the system (boy + swing) is at a certain height, which we denote as L. The time period of oscillation in this position is given as T.
3. Analyzing the Change in Position:
When the boy stands up, the center of mass of the system changes. The effective length L′ from the pivot to the new center of mass when the boy is standing is less than L because the boy's height is reduced relative to the swing's pivot.
4. Comparing Lengths:
Since the boy is now standing, the effective length L′<L.
5. Effect on Time Period:
Since the time period T is directly proportional to the square root of the length:
T′=2π√L′g
and since L′<L, it follows that:
T′<T
Therefore, the time period of oscillation when the boy stands up is less than T.
6. Conclusion:
The time period of oscillation of the swing when the boy stands up is less than T.
Final Answer:
The time period of oscillation of the swing when the boy stands up will be less than T.
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- L is the length from the pivot point to the center of mass of the pendulum,
- g is the acceleration due to gravity.
When the boy is sitting on the swing, the center of mass of the system (boy + swing) is at a certain height, which we denote as L. The time period of oscillation in this position is given as T.
When the boy stands up, the center of mass of the system changes. The effective length L′ from the pivot to the new center of mass when the boy is standing is less than L because the boy's height is reduced relative to the swing's pivot.
Since the boy is now standing, the effective length L′<L.
Since the time period T is directly proportional to the square root of the length:
T′=2π√L′g
and since L′<L, it follows that:
T′<T
Therefore, the time period of oscillation when the boy stands up is less than T.
The time period of oscillation of the swing when the boy stands up is less than T.
The time period of oscillation of the swing when the boy stands up will be less than T.
Similar Questions
Knowledge Check
Time period of oscillation of a spring is 12 s on earth. What shall be the time period if it is taken to moon?
A6 sB12 sC36 sD72 s
The time period of oscillation of the block as shown in figure is
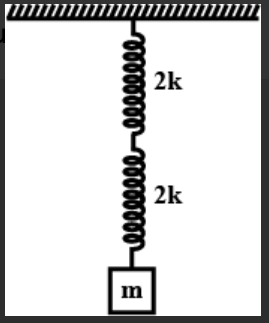
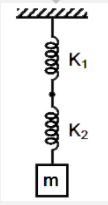
View SolutionTime period of oscillation for given combination will be :
View SolutionA boy is swinging in a swing. If he stands , the time period will
View SolutionA spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View SolutionThe time period of oscillations of a simple pendulum is 1 minute. If its length is increased b 44% then its new time period of oscillation will be
View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be

View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
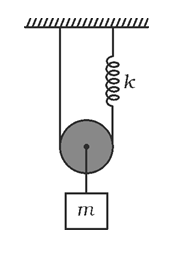
View Solution

_S01_040_Q01.png)