When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
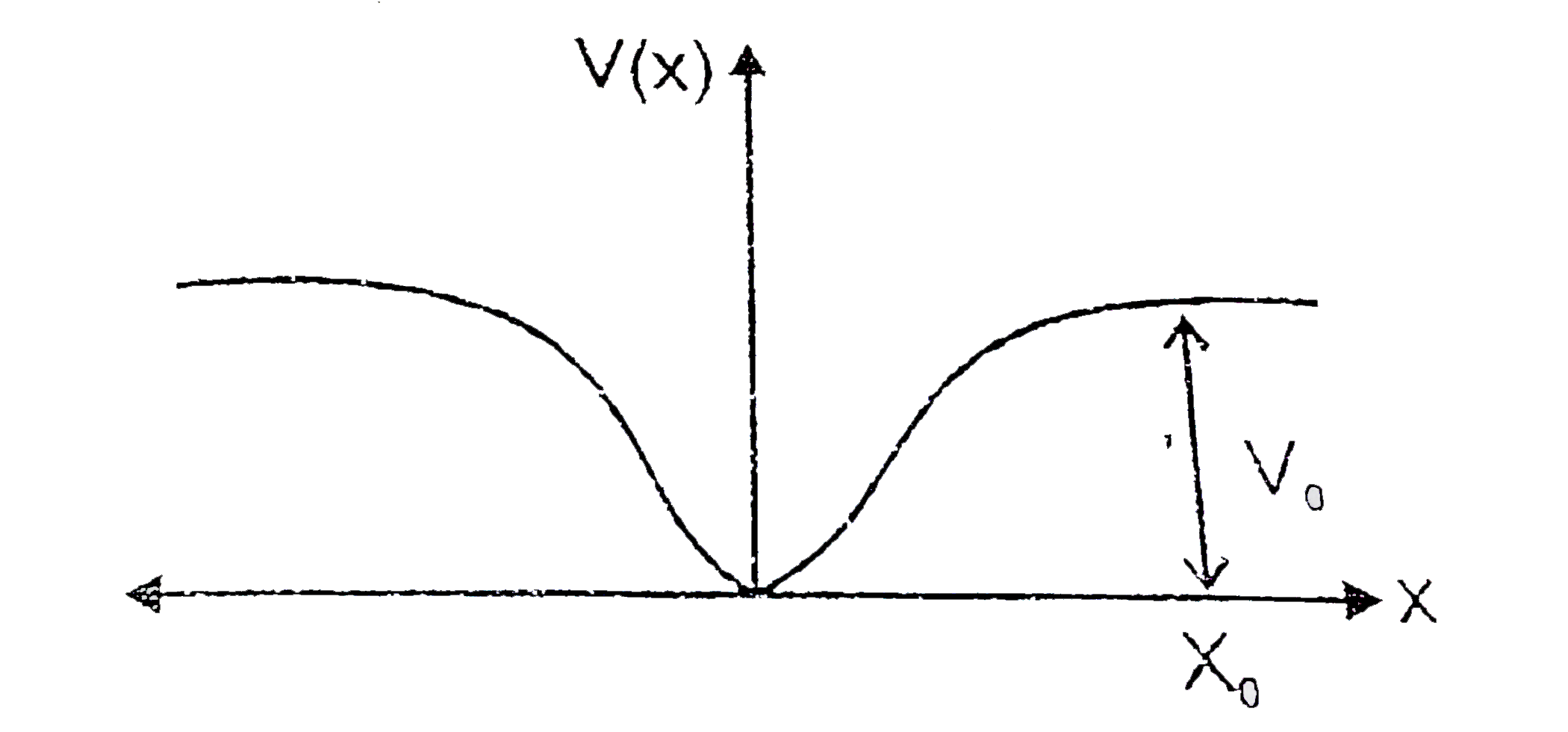
If the total energy of the particle is E, it will perform is periodic motion why if :
A
Elt0
B
E gt 0
C
V0>E>0
D
E>V0
Video Solution
Text Solution
The correct Answer is:C
If total energy E exceeds V0 then particle will continue to move up to infinity and thus periodic motion is not possible. Periodic motion is possible when V0>E>O, hence option (c ) is correct.
|
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (Matching Type Questions)
Explore 2 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (MATRIX MATCH TYPE QUESTIONS)
Explore 2 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (Multiple choice question)
Explore 11 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
Knowledge Check
When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=α⋅x4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :AE<0BE>0CV0>E>0DE>V0When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
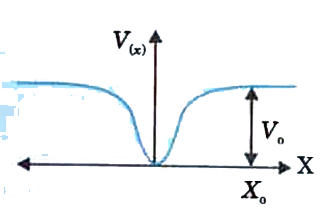
The acceleration of this particle for |X|>X0 isAproportional to (v0mX0)Bpropotinal to √V0mX0Cproportional to V0DZeroWhen a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
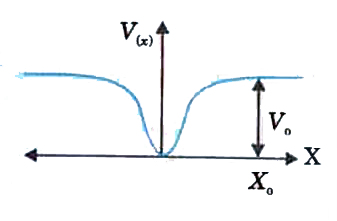
For periodic motion os small amplitude A . The time periodic T of this particle is proportional toAA√mαB1A√mαCA√αmD1A√αm
A particle moves on the X-axis according to the equation x=A+Bsinωt. Let motion is simple harmonic with amplitude
View SolutionA body is performing simple harmonic motion. Then its
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionIn simple harmonic motion, acceleration of the particle is zero, when its
View SolutionThe potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
View Solution