When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to √mk. As can be seen easily using dimensional analysis.

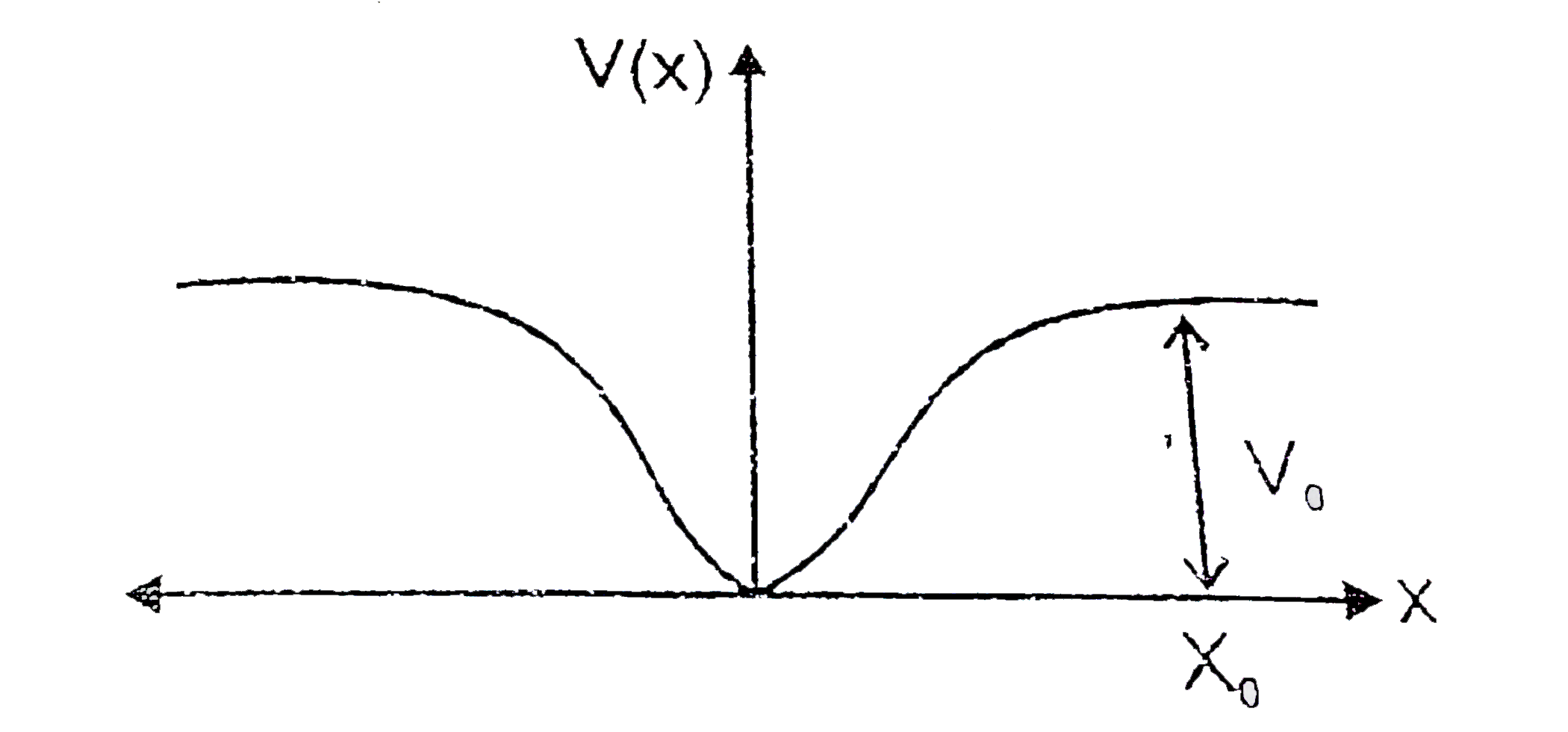
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=αx4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (See Fig).
The acceleration of this particle of |x|>X0 is :
proportional to V0
proportional to V0mX0
proportional to √V0mX0
zero.
The correct Answer is:D
Since, for |x|>X0.F=−dVdx=0.
So correct choice is (d).
Topper's Solved these Questions
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - MCQ (LEVEL-III) Questions From AIEEE/JEE Examination
10 Videos
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - RCQ
7 Videos
- OSCILLATIONSBOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - RCQ
7 Videos
- MOCK TEST-3BOOK - MODERN PUBLICATIONCHAPTER - MOCK TEST-3EXERCISE - MCQs
49 Videos
- PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS
17 Videos
Similar Questions
When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0)(seefigure).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_CHMO_C10_033_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Theae≤rationofthisparti≤for|x|gtX_(0)is<br>(a)∝rtional→V_(0)
(b) proportional to.
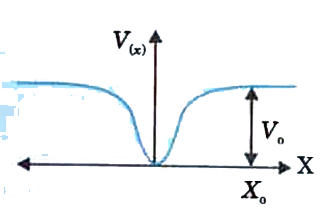
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
If the total energy of the particle is E, it will perform is periodic motion why if :
View Solution
Knowledge Check
When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
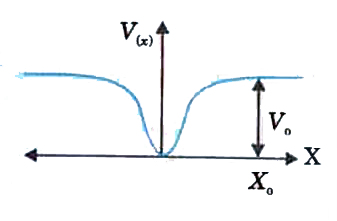
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
The acceleration of this particle for |X|>X0 isAproportional to (v0mX0)Bpropotinal to √V0mX0Cproportional to V0DZeroWhen a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
For periodic motion os small amplitude A . The time periodic T of this particle is proportional toAA√mαB1A√mαCA√αmD1A√αmWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=α⋅x4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :AE<0BE>0CV0>E>0DE>V0
When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionA particle moves on the x -axis according to the equation x=x0sin2ωt .The motion is simple harmonic ?
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View Solution
