When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 80cm and for rotation less than 1rev, what are the
(i) smallest and
(ii) largest angular speeds that cause the toast to hit and then topple to be butter-side down ?
smallest angular speed is 5π4rad/s and largest angular speed is 15π4rads.
smallest angular speed is π4rad/s and largest angular speed is 3π4rad/s
smallest angular speed is π2rad/s and largest angular speed is 3π2rad/s.
smallest angular speed is 5π2rad/s and largest angular speed is 15π2rad/s.
The correct Answer is:A
(a) The time it takes for the buttered toast to hit floor is.
Δt=√2hg=√2(8m)10m/s2=0.40s
The smallest angle turned for the toast to land butter - side down is Delatθmin=14rev=π/2. This corresponds to an angular speed of
ωmin=ΔθminΔt=π/2rad0.4s=5π4rad/s
The largest angle (less than 1 revolution) turned for the toast to land butter-side down is Δθmax=0.75rev=3π/2rad. This corresponds to an angular speed of
ωmax=ΔθmaxΔt=π/2rad0.4s=15π4rad/s.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Torque , Torque Equation And Equilibrium Of A Rigid Body29videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia39videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 76 cm and for rotation less than 1 rev, what are the (a) smallest and (b) largest angular speeds that cause the toast to hit and then topple to be butter-side down?
View SolutionA 100 turn closely wound circular coil of radius 10cm carries a current of 3⋅2A. (i) What is the field at the centre of the coil? (ii) What is the magnetic moment of this arrangement? The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of 2T in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through an angle of 90∘ under the influence of the magnetic field. (iii) What are the magnitudes of the torques on the coil in the initial and final positions? (iv) What is the angular speed acquired by the coil when it has rotated by 90∘? The moment of inertia of the coil is 0⋅1kgm2.
View Solution
Knowledge Check
- Question 1 - Select One or More
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
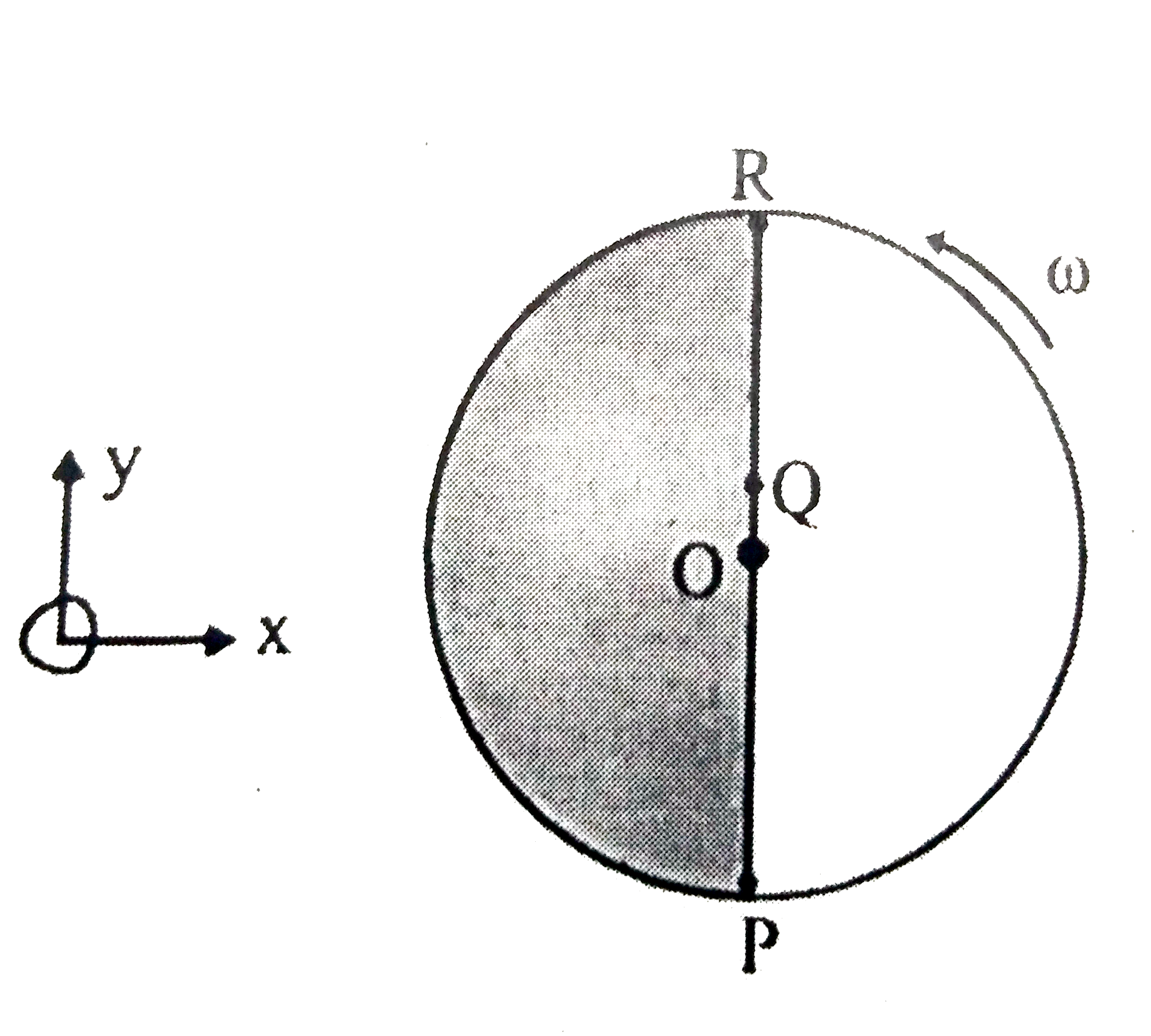 Ap lands in the shaded region and Q in the unshaded region.Bp lands in the unshaded region and Q in the shaded regionCBoth p and Q land in the unshaded region.DBoth p and Q Jand in the shaded region
Ap lands in the shaded region and Q in the unshaded region.Bp lands in the unshaded region and Q in the shaded regionCBoth p and Q land in the unshaded region.DBoth p and Q Jand in the shaded region - Question 2 - Select One
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
 Ap lands in the shaded region and Q in the unshaded region.BP landa in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region.
Ap lands in the shaded region and Q in the unshaded region.BP landa in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region. - Question 3 - Select One
Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
 AP lands in the shaded region and Q in the unshaded region.BP lands in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region.
AP lands in the shaded region and Q in the unshaded region.BP lands in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region.
Two discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?
View SolutionTwo discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident (i) What is the angular speed of the two-disc system ? (ii) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω1≠ω2.
View SolutionA uniform cubical block of mass M and side length L is lying on the edge of a rough table with 14th of its edge overhanging. When a small block of mass m is placed on its top surface at the right edge (see fig.), the cube is on verge of toppling. The block of mass m is given a sharp horizontal impulse so that it acquires a velocity towards B. The small block moves on the top surface and falls on the other side. What is maximum coefficient of friction between the small block and the cube so that the cube does not rotate as the block moves over it. Assume that the friction between the cube and the table is large enough to prevent sliding of the cube on the table.
 View Solution
View SolutionFigure 10-61 is an overhead view of a rod of length 1.0 m and mass 1.0 kg that is lying stationary on a frictionless surface when three bullets hit it simultaneously. The bullets move along paths that are in the plane of the rod and per-pendicular to the rod. Bullet 1 has mass 10 g and speed 2.0 m/s. Bullet 2 has mass 20 g and speed 3.0 m/s. Bullet 3 has mass 30 g and speed 5.0 m/s. The labelled distance are α=10cm, b = 60 cm, and c = 80 cm. As a result of the impacts, the rod-bullets system rotates around its center of mass while the center of mass moves in a straight line over the frictionless surface. (a) What is the linear speed of the system's center of mass? (b) What is the distance between the rod's center and the system's center of mass ? ( c) What is the rotational inertia of the system about the system's center of mass?
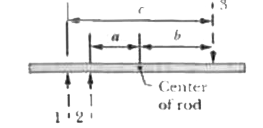 View Solution
View SolutionConsider a disc rotating in the horizontal plane with a constant angu lar speed ω about its centre O. the disc has shaded region on one side of the diameter and an unshaded region on the other side as shown in Fig. 5.111. when the disc is in the orientation as shown, two pebbles P and Q are simu ltaneously projected at an angle towards R. the velocity of projection in the y-z plane and is same for both pebbles with respect to the disc. Assume that i they land back on the disc before the disc has completed 1/8 rotation, ii their range is less than half the disc radus, and iii ω reamisn constant throughout. then
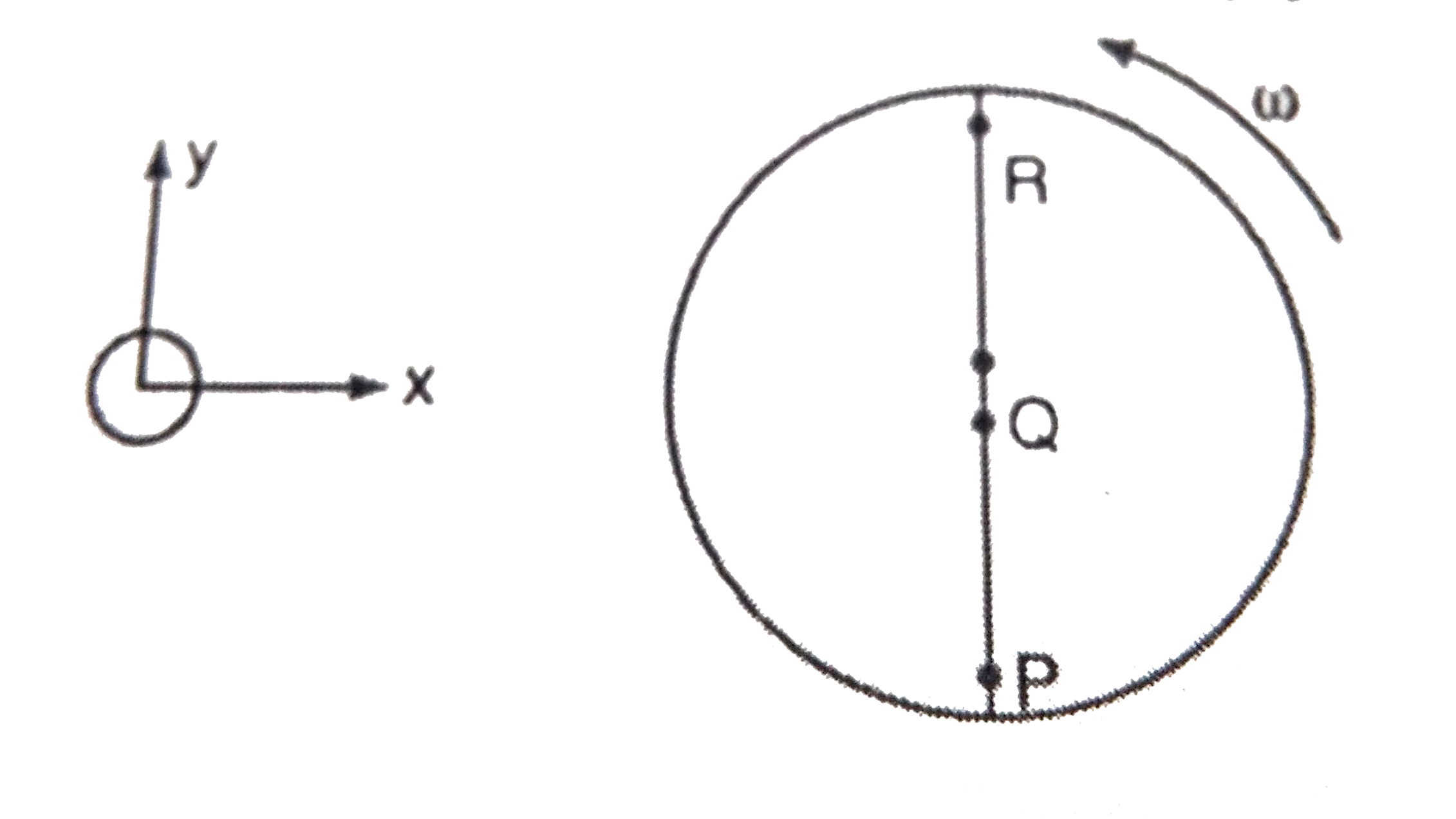 View Solution
View Solution

