When an automobile moving with a speed of 36km/h reaches an upward inclined road of angle 30∘, its engine is switched off. If the coefficient of friction is 0.1, how much distance will the automobile move before coming to rest ? Take g=10ms−2.
12.53m
21.42m
15.43m
8.53m
The correct Answer is:D
Given, initial speed, u=36km/h
=36×100060×60=10ms−1
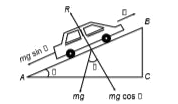
θ=30∘,μ=0.1s= ?
Here, work done in moving up the inclined road = KE of the vehicle
(mgsinθ+F)s=12mu2
(mgsinθ+μR)×s=12mu2
(mgsinθ+μmgcosθ)×s=12mu2
s=12μ2mg(sinθ+μcosθ)=u22g(sinθ+μcosθ)
=10×102×10×(sin30∘+0.1cos30∘)=8.53m
Topper's Solved these Questions
Similar Questions
When a car moving with a speed of 36km/h reaches an upwards inclined road of angle 30∘ its engine is switched off If coefficient of frition involved is 0.1 how much distance will the car move before coming to rest Giveng = 10m//s^(2).
View SolutionA block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
View Solution
Knowledge Check
When an automobile moving with a speed of 36km/h reaches an upward inclined road of angle 30∘, its engine is switched off. If the coefficient of friction is 0.1, how much distance will the automobile move before coming to rest ? Take g=10ms−2.
A12.53mB21.42mC15.43mD8.53mA conveyor belt is moving at a constant speed of 2m/s . A box is grenty dropped on it. Th ecoefficient of friction between them is μ=0.5 . The distance that the box will move relative to belt before coming to rest on it taking g=10ms−2 is:
A1.2mB0.6mCzeroD0.4mA conveyer belt is moving at a constant speed of 2 ms−1 A box is gently dropped on it. The coefficient of friction between them is μ = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g=10ms−2, is
A0.4mB1.2 mC0.6mDzero
An automobile moving at a speed of 72kmh−1 reaches the foot of a smooth incline, when the engine is switched off. How much distance does the automobile go up the incline before coming to rest. The angle of inclination with horizontal is 30∘ and g=9.8ms−2?
View SolutionA block of wood of 1 kg resting on an inclined plane of angle 30∘, just starts moving down. If the coefficient of friction is 0.2, then find its velocity (in ms−1) after 5 s (take , g=10ms−2)
View SolutionA suitcase is gently dropped on a conveyor belt moving at 3ms−1 If the coefficient of friction between the belt and suitcase is 0.5 how far will the suitcase move on the belt before coming to rest ?
View SolutionA block of wood of 1kg resting on an inclined plane a angle 30∘, just starts moving down. If the coefficient of friction is 0.2, then find its velocity (in ms−1) after 5s (take , g=10ms−2)
View SolutionConsider, a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the distance in which the car can be stopped is (Take g=10/s2)
View Solution
