When as proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We are given:
- Velocity of the proton: v=(2^i+3^j)×106m/s
- Force experienced by the proton: F=−1.28×10−13^k
Step 2: Use the Lorentz Force Equation
The force experienced by a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- q is the charge of the proton (q=1.6×10−19C)
- B is the magnetic field.
Step 3: Set Up the Cross Product
From the equation, we can express the cross product:
F=q(v×B)⇒−1.28×10−13^k=1.6×10−19((2^i+3^j)×B)
Step 4: Assume the Magnetic Field Direction
Let the magnetic field be in the negative ^j direction:
B=−B0^j
Step 5: Calculate the Cross Product
Now we calculate v×B:
v=(2^i+3^j)×106
B=−B0^j
Using the properties of the cross product:
v×B=(2^i+3^j)×(−B0^j)=−B0(2^i×^j+3^j×^j)
Since ^j×^j=0 and ^i×^j=^k:
v×B=−B0(2^k)=−2B0^k
Step 6: Substitute Back into the Force Equation
Substituting back into the force equation:
−1.28×10−13^k=1.6×10−19(−2B0^k)
This simplifies to:
−1.28×10−13=−3.2×10−19B0
Step 7: Solve for B0
Now, we can solve for B0:
B0=1.28×10−133.2×10−19=4T
Step 8: Write the Final Magnetic Field
Thus, the magnetic field B is:
B=−4^jT
Final Answer
The magnetic field is:
B=−4^jT
---
We are given:
- Velocity of the proton: v=(2^i+3^j)×106m/s
- Force experienced by the proton: F=−1.28×10−13^k
The force experienced by a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- q is the charge of the proton (q=1.6×10−19C)
- B is the magnetic field.
From the equation, we can express the cross product:
F=q(v×B)⇒−1.28×10−13^k=1.6×10−19((2^i+3^j)×B)
Let the magnetic field be in the negative ^j direction:
B=−B0^j
Now we calculate v×B:
v=(2^i+3^j)×106
B=−B0^j
Using the properties of the cross product:
v×B=(2^i+3^j)×(−B0^j)=−B0(2^i×^j+3^j×^j)
Since ^j×^j=0 and ^i×^j=^k:
v×B=−B0(2^k)=−2B0^k
Substituting back into the force equation:
−1.28×10−13^k=1.6×10−19(−2B0^k)
This simplifies to:
−1.28×10−13=−3.2×10−19B0
Now, we can solve for B0:
B0=1.28×10−133.2×10−19=4T
Thus, the magnetic field B is:
B=−4^jT
The magnetic field is:
B=−4^jT
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Video
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Video
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Video
Similar Questions
When a proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
View SolutionAn electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
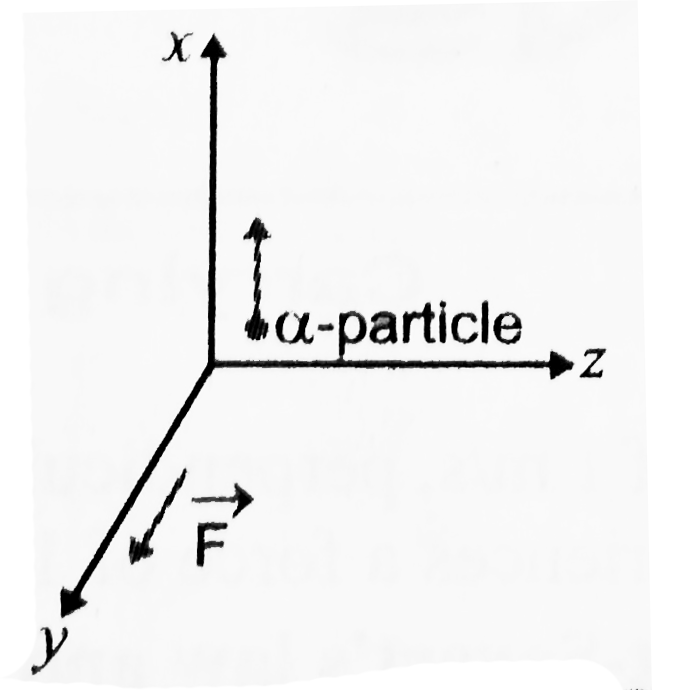
View SolutionA charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnetic field →B.
View SolutionA charged particle carrying charge q=1μc moves in uniform magnetic with velocity v1=106m/s at angle 45∘ with x-axis in the xy-plane and experiences a force F1=5√2N along the negative z-axis. When te same particle moves with velocity v2=106m/s along the z-axis it experiences a force F2 in y-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnitude of the force F2.
View SolutionA charged particle carrying charge q=10μC moves with velocity v1=106ms−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnitude of the force F2.
View SolutionA charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
View SolutionA charge q=4μC has as instantaneous velociyt v=(2ˆi−3ˆj+ˆk)×106ms in a uniform magnetic field B=(2ˆi+5ˆj−3ˆk)×10−2T. What is the force on the charge?
View SolutionA charge q moves with a velocity 2m/s along x- axis in a unifrom magnetic field B=(ˆi+2ˆj+3ˆk) tesla.
View SolutionA point charge of 5×10−6C experiences a force of 2×10−3N when kept in a uniform electric field of intensity E. Find E.
View Solution
