When light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv−ϕ) is the maximum kinetic energy of emitted photoelectron (where ϕ is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tuve. Wavelength of charasteristic X-ray depends on the atomic number.
Q. A monochromatic light is used in a photoelectric experiment on photoelectric effect. The stopping potential
is related to the mean wavelength
is related to the shortest wavelength
is related to the maximum kinetic energy of emitted photoelectrons
intensity of incident light
The correct Answer is:B, C
To solve the problem regarding the photoelectric effect and the stopping potential, we will follow these steps:
Step 1: Understand the Photoelectric Effect
The photoelectric effect occurs when light of sufficient frequency strikes a metallic surface, causing the emission of electrons. The energy of the incident photons is given by E=hν, where h is Planck's constant and ν is the frequency of the light.
Step 2: Relate Photon Energy to Work Function
The maximum kinetic energy (KEmax) of the emitted photoelectrons can be expressed using Einstein's photoelectric equation:
KEmax=hν−ϕ
where ϕ is the work function of the metal.
Step 3: Define Stopping Potential
The stopping potential (V0) is the potential difference needed to stop the emitted electrons from reaching the anode. The relationship between the stopping potential and the maximum kinetic energy is given by:
KEmax=eV0
where e is the charge of the electron.
Step 4: Combine the Equations
From the above equations, we can equate the maximum kinetic energy to the stopping potential:
eV0=hν−ϕ
Rearranging gives:
V0=hν−ϕe
Step 5: Relate Stopping Potential to Wavelength
Using the relation ν=cλ (where c is the speed of light and λ is the wavelength), we can substitute hν with hcλ:
V0=hc/λ−ϕe
This can be rewritten as:
V0=hceλ−ϕe
Step 6: Analyze the Options
Now we can analyze the statements regarding the stopping potential:
1. Stopping potential is related to the mean wavelength - This is incorrect; it is related to the maximum kinetic energy.
2. Stopping potential is related to the maximum kinetic energy of emitted photoelectrons - This is correct.
3. Stopping potential depends on the intensity of incident light - This is incorrect; intensity affects the number of emitted electrons, not their energy.
Conclusion
The stopping potential is primarily related to the maximum kinetic energy of the emitted photoelectrons, not to the intensity of the light or the mean wavelength.
The photoelectric effect occurs when light of sufficient frequency strikes a metallic surface, causing the emission of electrons. The energy of the incident photons is given by E=hν, where h is Planck's constant and ν is the frequency of the light.
The maximum kinetic energy (KEmax) of the emitted photoelectrons can be expressed using Einstein's photoelectric equation:
KEmax=hν−ϕ
where ϕ is the work function of the metal.
The stopping potential (V0) is the potential difference needed to stop the emitted electrons from reaching the anode. The relationship between the stopping potential and the maximum kinetic energy is given by:
KEmax=eV0
where e is the charge of the electron.
From the above equations, we can equate the maximum kinetic energy to the stopping potential:
eV0=hν−ϕ
Rearranging gives:
V0=hν−ϕe
Using the relation ν=cλ (where c is the speed of light and λ is the wavelength), we can substitute hν with hcλ:
V0=hc/λ−ϕe
This can be rewritten as:
V0=hceλ−ϕe
Now we can analyze the statements regarding the stopping potential:
1. Stopping potential is related to the mean wavelength - This is incorrect; it is related to the maximum kinetic energy.
2. Stopping potential is related to the maximum kinetic energy of emitted photoelectrons - This is correct.
3. Stopping potential depends on the intensity of incident light - This is incorrect; intensity affects the number of emitted electrons, not their energy.
The stopping potential is primarily related to the maximum kinetic energy of the emitted photoelectrons, not to the intensity of the light or the mean wavelength.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer
9 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Single Correct Answer Type
7 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
When light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv−ϕ) is the maximum kinetic energy of emitted photoelectron (where ϕ is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tuve. Wavelength of charasteristic X-ray depends on the atomic number.
Q. If potential difference across the tube is increased then
View SolutionWhen light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv−ϕ) is the maximum kinetic energy of emitted photoelectron (where ϕ is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tuve. Wavelength of charasteristic X-ray depends on the atomic number.
Q. If frequency (υ>υ0) of incident light becomes n times the initial frequency (v), then KE of the emitted photoelectrons becomes (v0 threshold frequency).
View Solution
Knowledge Check
A light of wavelength 600 nm is incident on a metal surface. When light of wavelength 400 nm is incident, the maximum kinetic energy of the emitted photoelectrons is doubled. The work function of the metals is
A1.03 eVB2.11 eVC4.14 eVD2.43 eVThe photoeletric threshold 4v is incident on the metal is v. When light of freqency 4v is incident on the metal, the maximum kinetic energy of the emitted photoelectron is
A4hvB3hvC5hvD5hv2
Light of wavelength 4000A∘ is incident on a metal surface. The maximum kinetic energy of emitted photoelectron is 2 eV. What is the work function of the metal surface?
View SolutionIf the frequency of light in a photoelectric experiment is double then maximum kinetic energy of photoelectron
View SolutionPhotons of energy 6eV are incident on a metal surface whose work function is 4eV. The minimum kinetic energy of the emitted photo - electrons will be
View SolutionThe kinetic energy of photoelectrons emitted by a photosensitive surface depends on the internsity of the incident radiation
View SolutionThe frequency of incident light falling on a photosensitive metal plate is doubled, the KE of the emitted photoelectrons is
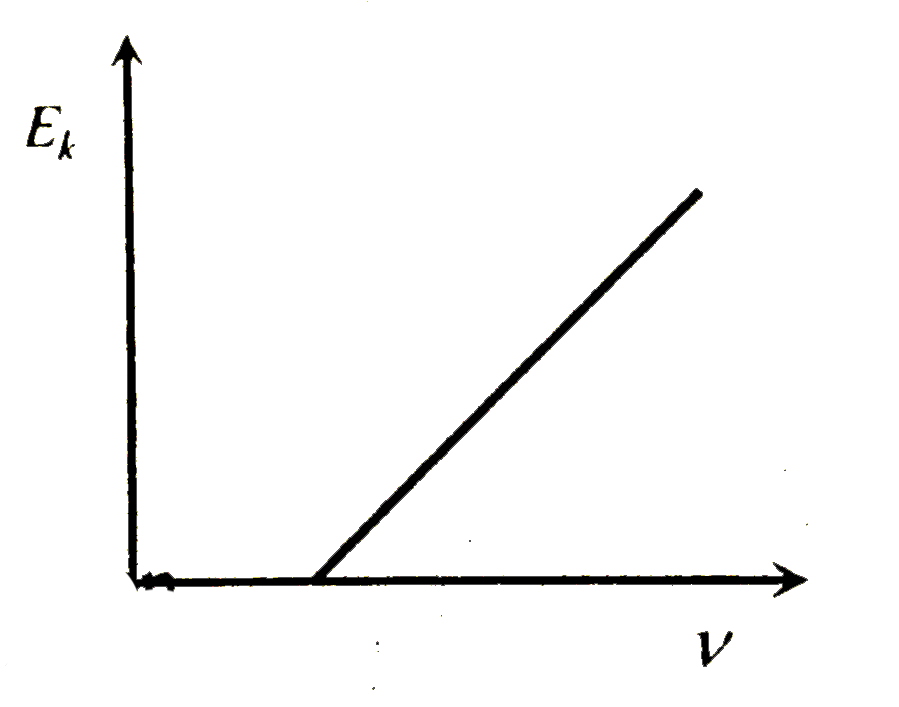
View SolutionFor the photoelectric effect, the maximum kinetic energy Ek of the emitted photoelectrons is plotted against the frequency of the incident photons as shown in the figure. The slope of the curve gives
View Solution
