When the positively charged hanging pendulum bob is made fixed, the work done in slowly shifting a unit positive charge from infinity to P is V. If the pendulum is free to move, the corresponding work done id V'. Then.
V=V'
V>V'
V<V'
V≤V'
The correct Answer is:b
To solve the problem, we need to establish a relationship between the work done in bringing a unit positive charge from infinity to a point P when a positively charged pendulum bob is fixed (denoted as V) and when the pendulum bob is free to move (denoted as V′).
1. Understanding the Fixed Pendulum Case:
- When the pendulum bob is fixed, it has a positive charge +Q.
- The work done V in bringing a unit positive charge +1 from infinity to point P is given by the formula for electric potential energy:
V=k⋅Q⋅1r
- Here, k is Coulomb's constant, Q is the charge of the pendulum bob, and r is the distance from the charge to point P.
2. Understanding the Free Pendulum Case:
- When the pendulum bob is free to move, it will experience a repulsive force due to the positive charge +Q.
- This repulsion will cause the pendulum to move away from point P, increasing the distance from r to r′ (where r′>r).
- The work done V′ in this case is:
V′=k⋅Q⋅1r′
3. Comparing the Two Cases:
- Since r′>r, it follows that:
1r′<1r
- Therefore, we can conclude:
V′<V
- This implies that the work done V′ when the pendulum is free to move is less than the work done V when it is fixed.
4. Final Relationship:
- The final relationship we establish is:
V>V′
Conclusion:
The work done in bringing a unit positive charge from infinity to point P when the pendulum bob is fixed is greater than the work done when the pendulum bob is free to move.
- When the pendulum bob is fixed, it has a positive charge +Q.
- The work done V in bringing a unit positive charge +1 from infinity to point P is given by the formula for electric potential energy:
V=k⋅Q⋅1r
- Here, k is Coulomb's constant, Q is the charge of the pendulum bob, and r is the distance from the charge to point P.
- When the pendulum bob is free to move, it will experience a repulsive force due to the positive charge +Q.
- This repulsion will cause the pendulum to move away from point P, increasing the distance from r to r′ (where r′>r).
- The work done V′ in this case is:
V′=k⋅Q⋅1r′
- Since r′>r, it follows that:
1r′<1r
- Therefore, we can conclude:
V′<V
- This implies that the work done V′ when the pendulum is free to move is less than the work done V when it is fixed.
- The final relationship we establish is:
V>V′
The work done in bringing a unit positive charge from infinity to point P when the pendulum bob is fixed is greater than the work done when the pendulum bob is free to move.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Knowledge Check
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
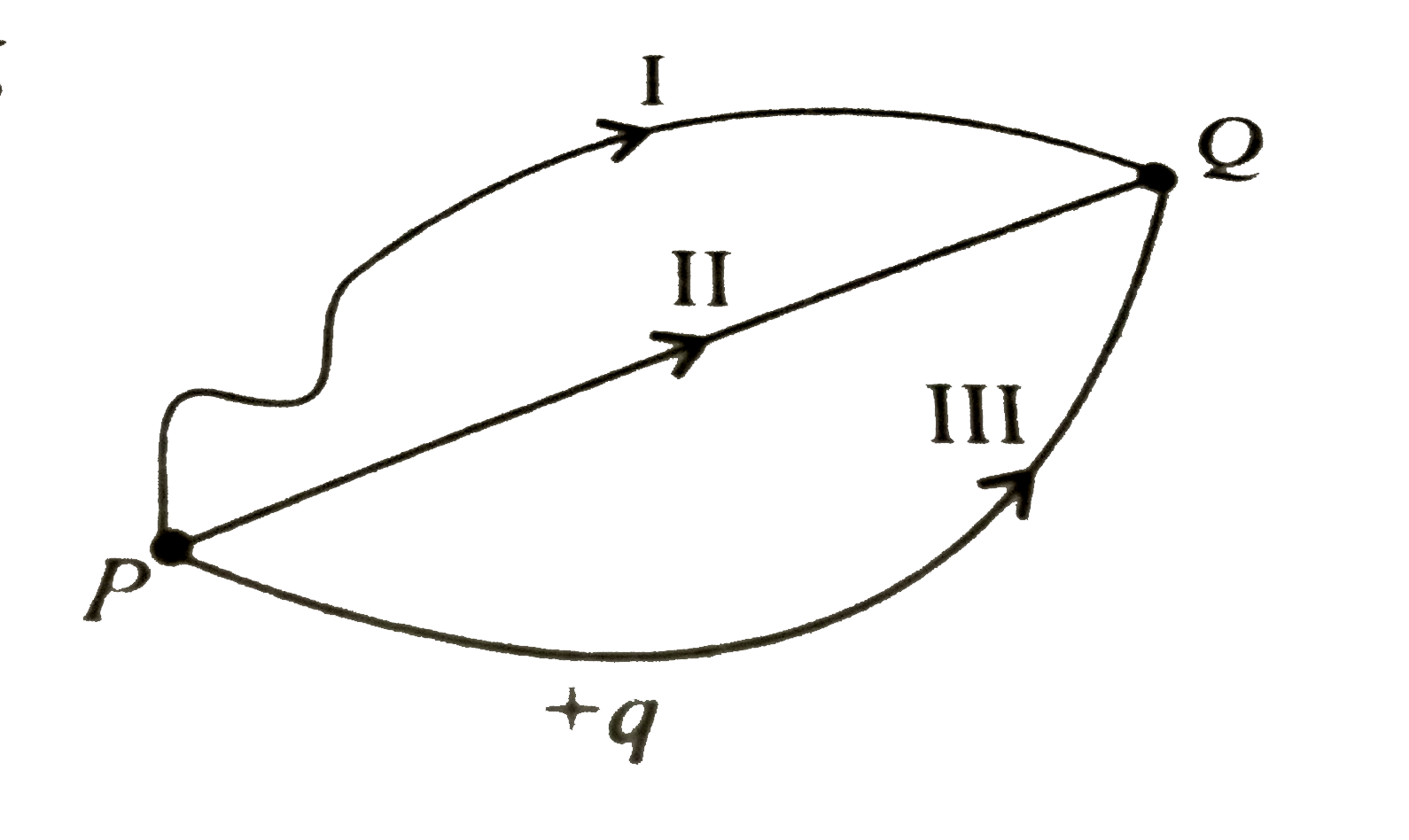
AWQxBWCWxDWQThe work done to move a unit charge along an equipotential from P to Q
Amust be defined as −Q∫P→E.→dlBis zeroCcan have a non-zero valueDboth (a) and (b)are correct
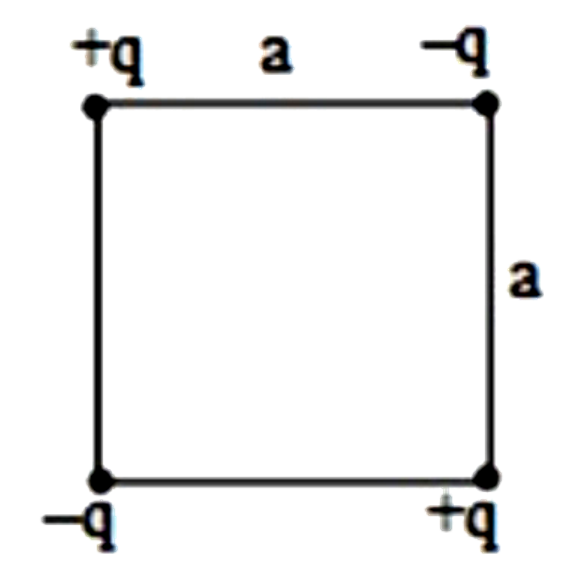
The work required to put the four charges from infinity to the position shown here is
View Solutionwhen the bob of a simple pendulum swings, the work done by tension in the string is :
View SolutionFind the work done by some external force in moving a charge q=2μC from infinity to a point where electric potential is 104 V.
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionThe work done to move a charge along an equipotential from A to B
View SolutionFind the work done by some external force in moving a charge q=4μC from infinity to a point, where electric potential is 104V
View Solution

 .
.