Which of the figure's six arrangements correctly show the vector addition of forces →F1 and →F2 to yield the third vector, which is meant to represent their net force →Fnet ?

Video Solution
Text Solution
c, d, and e (→F1 and →F2 must be head to tail, →Fnet must be from tail of one of them to head of the other)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS52videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)36videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the four arrangements in the figure correctly shows the vector addition of two forces →F1 and →F2 to yield the third force →F3
A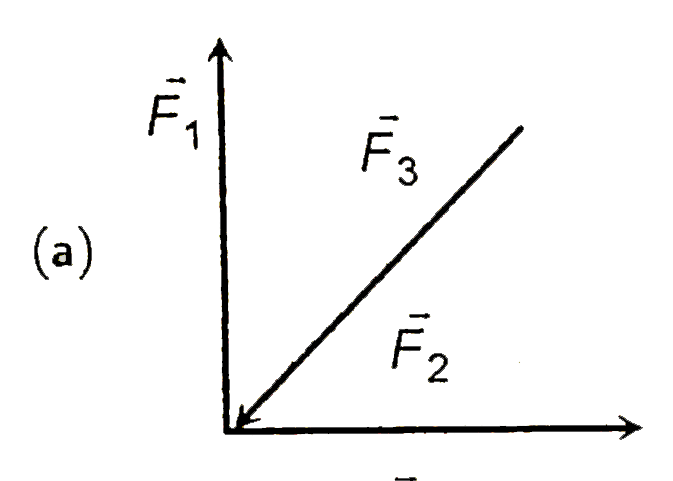 B
B C
C D
D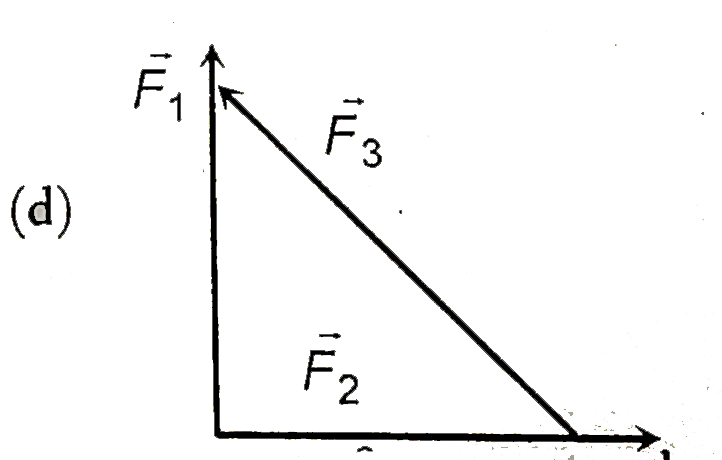
- Question 2 - Select One
Which of the four arrangements in the figure correctly shows the vector addition of two forces F1 & F2 to yield the third force F3?
A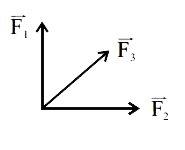 B
B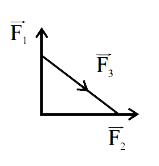 C
C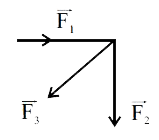 D
D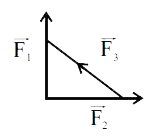
- Question 3 - Select One
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2
Two forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View SolutionA body is moving under the action of two force −→F1=2ˆi−5ˆj , −→F2=3ˆi−4ˆj . It's velocity will become uniform under a third force −→F3 given by.
View SolutionThe vector →a lies in the plane of vectors →band→c. Which one of the following is correct ?
View SolutionIf the vector →a lies in the planar of vectors →band→c, then which one of the following is correct?
View SolutionConsider a vector →F=4ˆi−3ˆj. Another vector that is perpendicular to →F is
View Solution

