Which of the following depend on whether rays are paraxial or not for spherical mirrors ?
Pole
Principal axis
Radius of curvature
Focus
The correct Answer is:D
Focal length is half the radius of curvature for paraxial rays. Or in general focal length depends on height of the ray above principal axis.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS)21videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)40videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Numerical Problems)36videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Which of the following entities related to spherical mirrors do not depend on whether rays are paraxial or not ?
APoleBPrincipal axisCRadius of curvatureDfocal length - Question 2 - Select One
Which of the following correctly depicts the reflection of a ray of light on a spherical mirror?
A
B
C
D
- Question 3 - Select One
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence θ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle θ shown in figure as follows :
f=R−R2secθ
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
Let fP and fm represent the focal length corresponding to paraxial rays and marginal rays respectively thenALet fp and fm represent the focal length corresponding to paraxial rays and marginal rays respectively thenBfp=fmCfp>fmDfp<fm
Plane Mirror||Spherical Mirror
View SolutionCan a plane mirror be called spherical mirror?
View Solution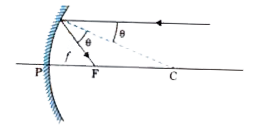
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence θ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle θ shown in figure as follows :
f=R−R2secθ
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
For paraxial rays focal length is approximatelyView Solution
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence θ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle θ shown in figure as follows :
f=R−R2secθ
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
What will be the focal length for ray which is incident at an angle 60∘?View SolutionWhich of the following statements are incorrect for spherical mirror.
View Solution