Which of the following potential energy curves in figure., cannot possibley describly describe the elastic collision of two billiard balls ? Here r is distance between centres of the balls.

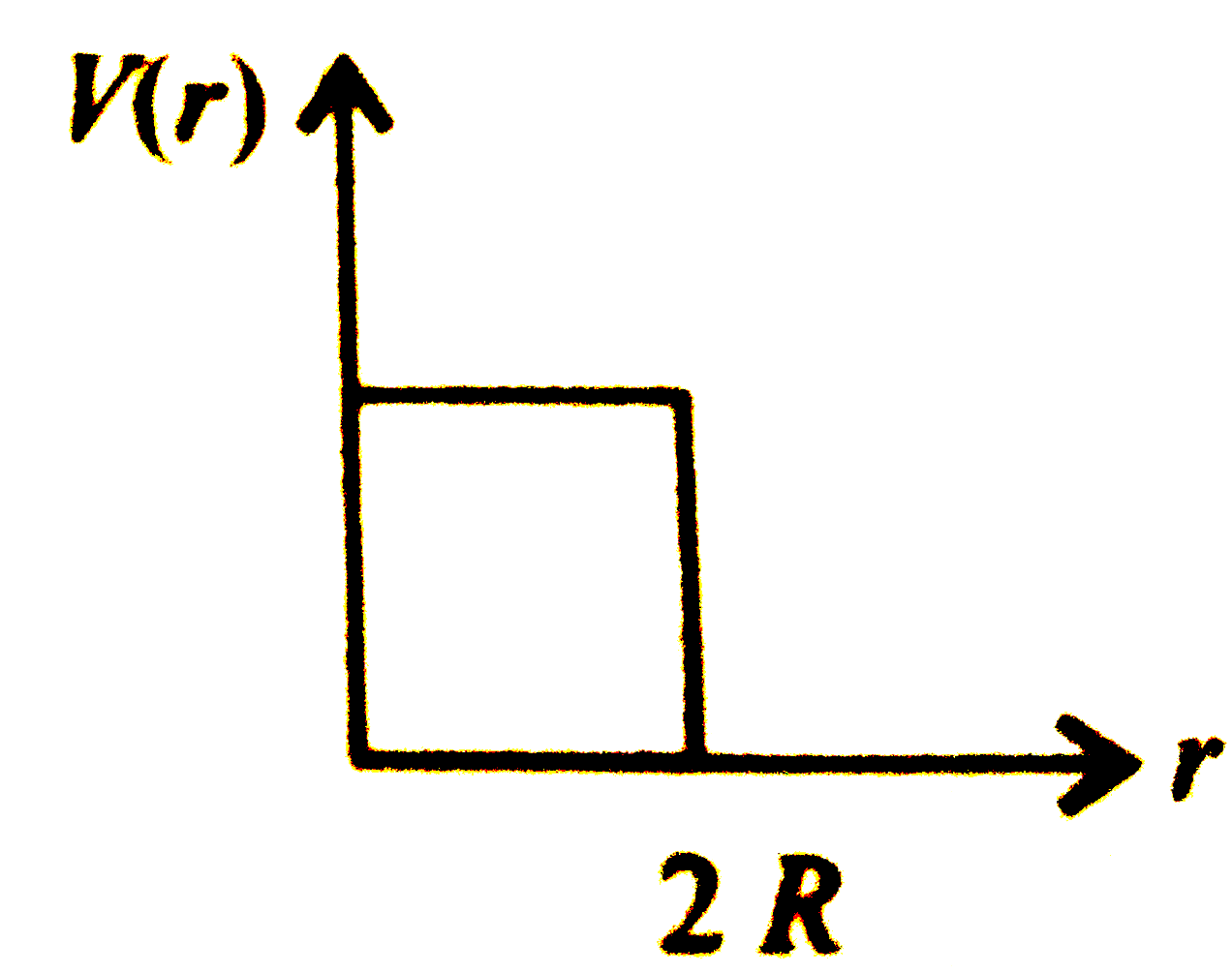
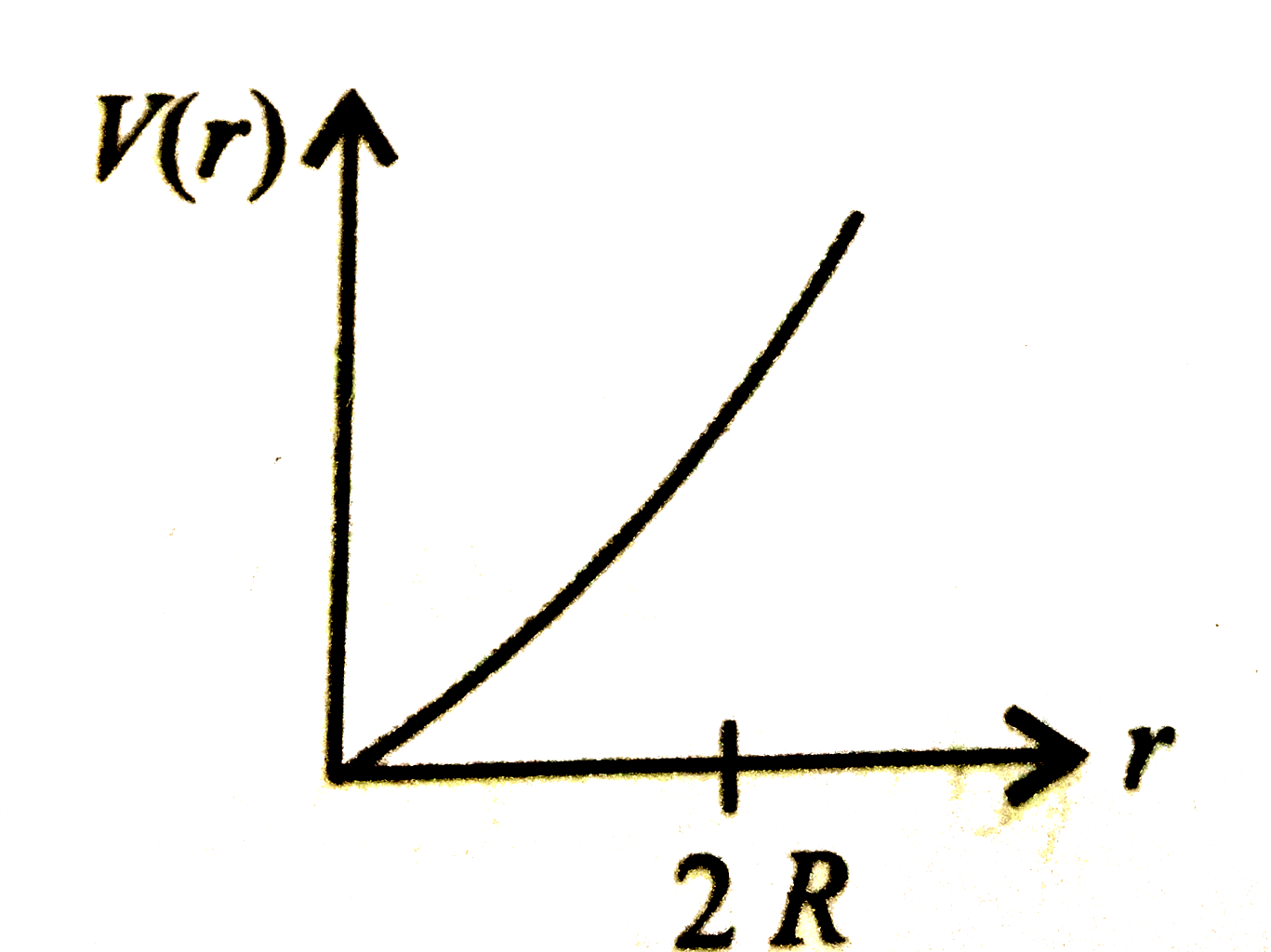
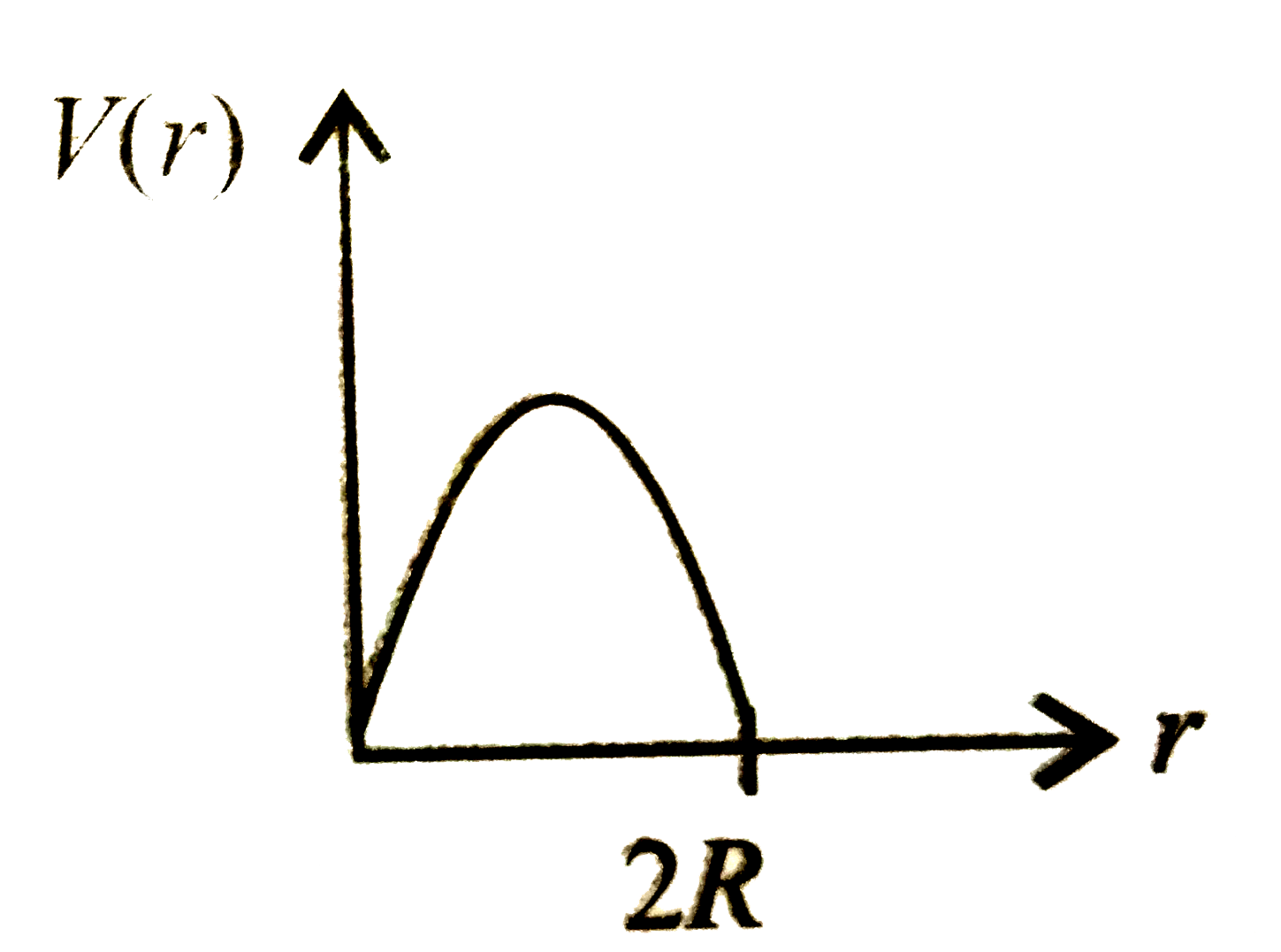
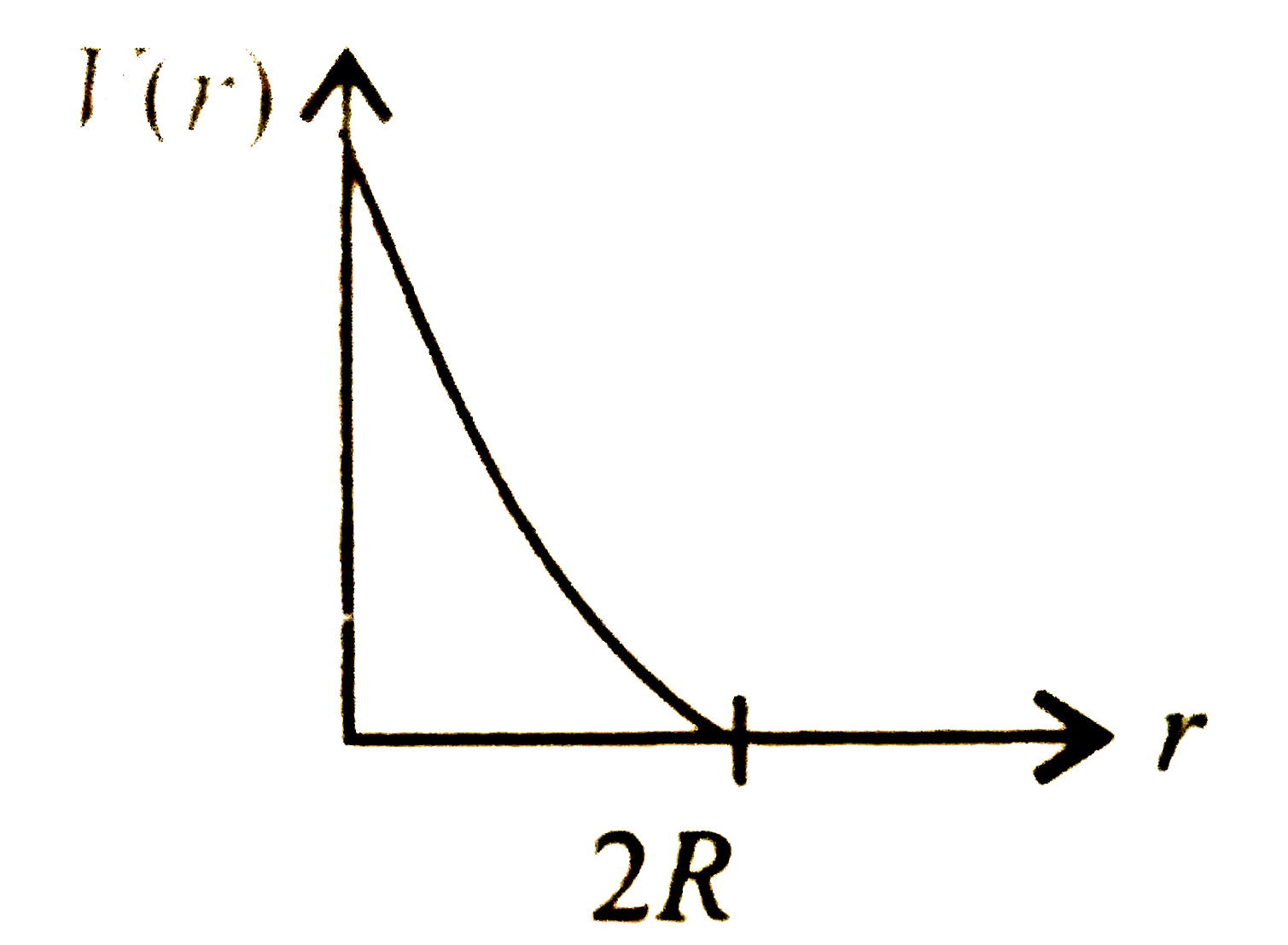
The correct Answer is:C
The potential energy of a system of two masses varies inversely as the distance (r) between them.
i.e. V(r)∝1r
When the two billiard balls touch each other potential energy becomes zero, i.e at r=R+R=2R,V(r)=0
Out of the given graphs, only curve (c ) satisfies these conditions. Therefore, all other curves cannot possibly describe the elastic collision of two billiard balls.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT18videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON15videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
Similar Questions
During elastic collision of two balls, is kinetic energy conserved during the short interval of contact of balls ?
View SolutionAnwer carefully, with reasons:
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
c) What are the answers to a) and b) for an inelastic collision?
d) If the potenital energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic? (note we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).View SolutionAssertion: Collisionn between two billiard's ball are inelastic
Reason: Momentum remains conserve during the collision.View SolutionIn an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact).
(a) Kinetic energy . (b) Total linear momentum ?
Give reason for your answer in each case.View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
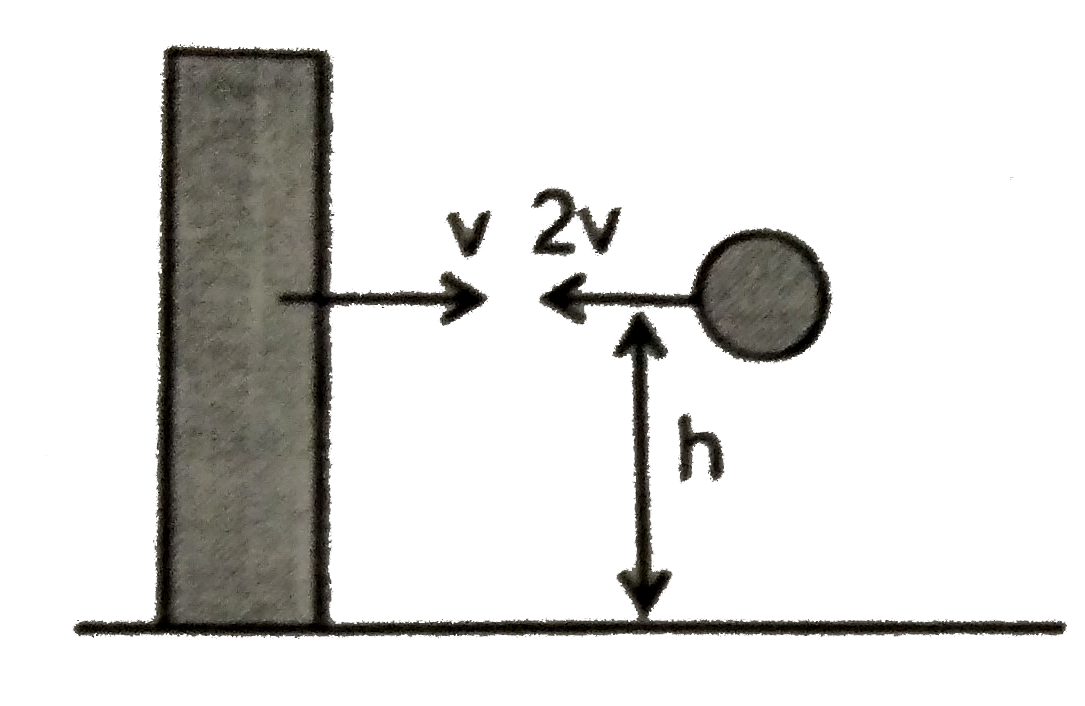 View Solution
View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centers at (0, 0, R) and at (5R, -R, R) respectively, in a coordinate system as shown. Ball A, moving along positive x axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the ball is elastic.

Impulse of the force exerted by A and B during the collision, is equal toView SolutionThe potential energy curve for interaction between two molecules is shown in figure. Which of the following statements are true?
View SolutionTwo identical balls are rolling without slipping on a horizontal plane as shwon in figure. They undergo a perfect elastic collision. Just after collision, the velocity of image of the bottom point of A with respect to the plane mirros is x V, then x=
 View Solution
View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centre at (0,0,R) and (5R,-R,R) respectively, in a coordinate system as shown. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the balls is elastic. Velocity of the ball A just after the collsion is
A. (ˆi+√3ˆj)m/s
B. (ˆi−√3ˆj)m/s
C. (2ˆi+√3ˆj)m/s
D. (2ˆi+2ˆj)m/sView SolutionTwo balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.
 View Solution
View Solution

