Which of the following statement (s) is/are true?

A

In vaccum the speed of red colour is more than that of violet colour

B

An object in front of a mirror is moved towards the pole of a spherical mirror from infinity, it is found that image also moves towards the pole. The mirror must be convex

C

There exist two angles of incidence in a prism for which angles of deviation are same except minimum deviation

D

A ray travels from a rarer medium to denser medium. There exist three angles of incidence for which the deviation is same

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B, C

(a) If vacuum speed of light of all colours is same.
(b) ocr_image
If object moves from ∞→P, then its vertual,
erect and diminished image move from F to P.
(c) 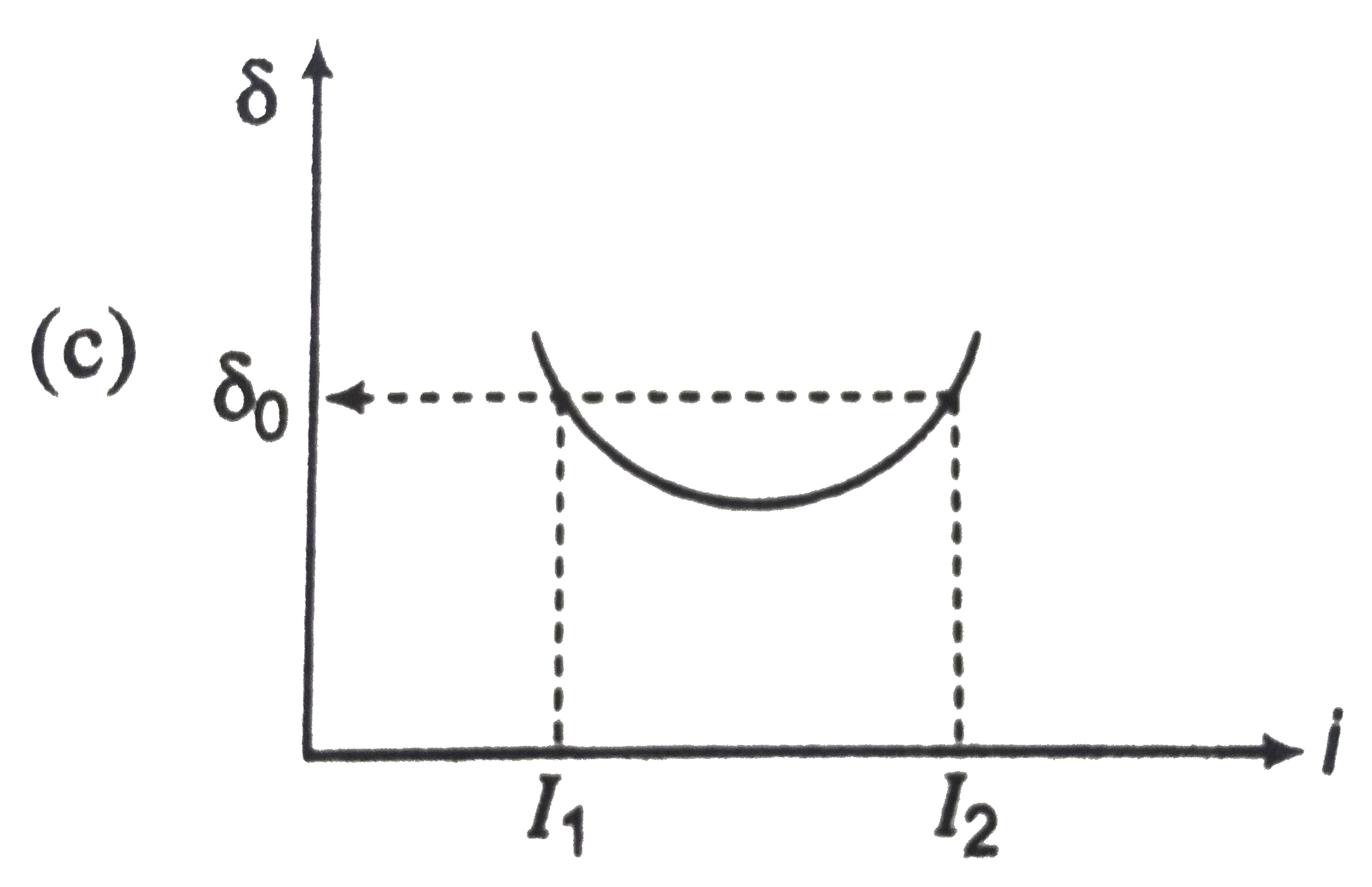ocr_image

Updated on:21/07/2023
|
Class 12PHYSICSGEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Which of the following statements (s)is/are true?

    Aa) Differentiable function satisfying f(−1)=f(1) and f'(x)≥0 for all x must be a constant function on the interval [−1,1].
    Bb) There exists a function with domain R satisfying f(x) lt 0, for all x, f'(x) gt 0 for all x and f''(x0 gt 0 for all x.
    Cc) If f''(x) = 0 then (c,f(c)) is an inflection point.
    Dd) Suppose f(x) is a function whose derivative is the function f(x)=2x2+2x−12. Then f(x) is decreasing for −3<x<2 and concave up for x>−12.

  • Which of the following statements (s) is/are true ?

    Aa) Differentiable function satisfying f(−1)=f(1) and f'(x)≥0 for all x must be a constant function on the interval [−1,1].
    Bb) There exists a function with domain R satisfying f(x) lt 0, for all x, f'(x) gt 0 for all x and f''(x0 gt 0 for all x.
    Cc) If f''(x) = 0 then (c,f(c)) is an inflection point.
    Dd) Suppose f(x) is a function whose derivative is the function f(x)=2x2+2x−12. Then f(x) is decreasing for −3<x<2 and concave up for x>−12.

  • Which of the following statements (s) is/are true?

    Alimx→aax−xaxx−aa=−1 then a is 1
    Blimn→∞logn−1n.Logn(n+1)n.log(n+1)(n+2)………log(n5−1)n5=5
    Climx→nlogx2+1x+1(√x2+1−x)=1
    Dlimx→0y→0x2y=0, when (x,y) → (0,0) along the curve y2=x3